Uitwerkingen opgaven hoofdstuk 2

Uitwerkingen opgaven hoofdstuk 2
2.1
Opgave 1
Opgave 2
Horizontale worp
Vlak voordat het pakje uit de helikopter valt, heeft het pakje dezelfde
voorwaartse snelheid als de piloot van de helikopter. Als de helikopter met
dezelfde snelheid door blijft vliegen, ziet de piloot het pakketje dus recht naar
beneden vallen.
In de praktijk zal de voorwaartse snelheid van het pakje afnemen ten gevolge
van de luchtweerstand. Het pakje zal daardoor geleidelijk achterblijven bij de
helikopter.
a Als de bal de grond treft, heeft de bal zich in verticale richting omlaag
verplaatst over een afstand van 1,6 m
y (t )  12  g  t 2 

2
2
1
y  1, 6 m
  1, 6  2  9,81  t  t  0,3262  tval  0,57 s
g  9,81 m/s 2 
b vy  g  tval 

tval  0,57 s   vy  9,81  0,57  5, 6 m/s
g  9,81 m/s 2 

c In horizontale richting werken er geen krachten, dus geldt de eerste wet van
Newton. De horizontale snelheid vx is dus 6,0 m/s.
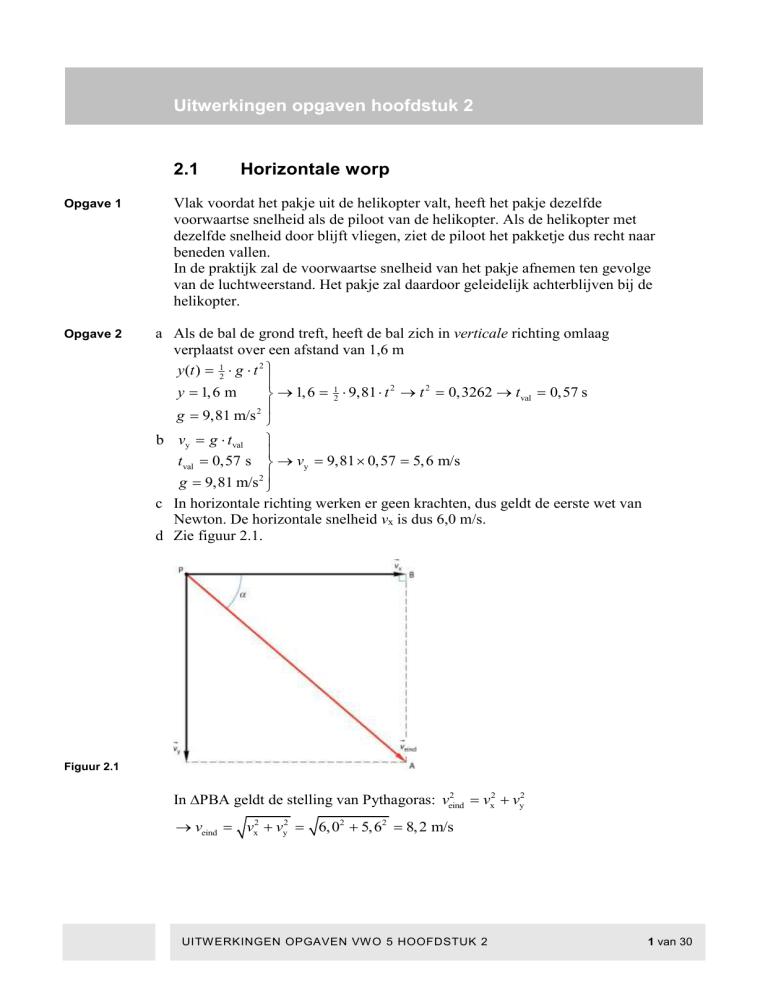
d Zie figuur 2.1.
Figuur 2.1
2
In ∆PBA geldt de stelling van Pythagoras: veind
 vx2  vy2
 veind  vx2  vy2  6, 02  5, 62  8, 2 m/s
UITW ERKINGEN OPGAVEN VW O 5 HOOFDSTUK 2
1 van 30
e Zie figuur 2.1.
In ΔPBA:
PB vx 6, 0
cos  


   43
PA v 8, 2
of
BA vy 5, 6
sin  


   43
PA
v 8, 2
of
BA vy 5, 6
tan  


   43
PB vx 6, 0
Opgave 3
a Als de bal de grond treft, heeft de bal zich in verticale richting omlaag
verplaatst over een afstand van 2,6 m
2

sy (t )  12  g  tval

2
2
sy (t )  2, 6 m   2, 6  12  9,81  tval
 tval
 0,5301  tval  0, 73 s

g  9,81 m/s 2 
b De horizontale beweging gebeurt met constante snelheid:
sx (t )  vx  tval 

vx  17 m/s   sx  17  0, 73  12 m
tval  0, 73 s 

c Eerste manier (met bewegingsvergelijkingen)
vx  17 m/s
vy  g  tval


tval  0, 73 s   vy  9,81  0, 73  7,16 m/s

g  9,81 m/s 2 
2
De stelling van Pythagoras: veind
 vx2  vy2
 veind  vx2  vy2  172  7,162  18 m/s
Tweede manier (met de energiebalans)
Eboven = Eeind
Ezw,boven + Ekin,boven = Ek,eind
2
2
m  g  h  12  m  vboven
 12  m  veind
2
2
 12  veind
Delen door m levert: g  h  12  vboven
h  sy  2, 6 m


2
2
1
1
  9,81  2, 6  2  17  2  veind
vboven  vx  17 m/s 

2
veind  340
veind  18 m/s
Opgave 4
a Zie figuur 2.2.
In verticale richting verplaatst Piet-Hein zich over een afstand van 1,20 m
 sy = 1,20 m
UITW ERKINGEN OPGAVEN VW O 5 HOOFDSTUK 2
2 van 30
2

sy (t )  12  g  tspring

2
1
  1, 20  2  9,81  tspring  tspring  0, 4946 s
sy (t )  1, 20 m 

Figuur 2.2
In horizontale richting beweegt Piet-Hein met constante snelheid
sx (t )  vx  tspring 

sx  2, 00 m
  2, 00  vx  0, 4946
tspring  0, 4946 s 
vx,minimaal = 4,04 m/s
b We beschouwen de (draai)momenten ten opzichte van de linkerdrijver. Het
moment ‘linksom’ ten gevolge van het gewicht van Piet-Hein is groter dan het
moment ‘rechtsom’ ten gevolge van het gewicht van het vlot. Daarom gaat het
vlot ‘linksom’ draaien en klapt het Piet-Hein in het gezicht.
Opgave 5
a In verticale richting verplaatsen de kinderen zich over een afstand van 80 cm
2

sy (t )  12  g  tval

2
1
  0,80  2  9,81  tval  tval  0, 404 s
sy (t )  0,80 m 

In horizontale richting bewegen de kinderen met constante snelheid over een
maximale afstand van 1,0 m
sx (t )  vx,max  tval 

sx  1, 0 m
  1, 0  vx,max  0, 404
tval  0, 404 s 
vx,max = 2,5 m/s
b De energiebalans: Eboven = Eeind
Ezw,boven = Ekin,eind
2
m  g  h  12  m  veind
Delen door m levert:
2
g  h  12  veind
9,81  h  12  2,52
 ∆h = 0,312 m
 de hoogte h van de glijbaan ten opzichte van het wateroppervlak =
0,80 + 0,312 = 1,11 m
c Als er sprake is van luchtweerstand, dan komt niet alle zwaarte-energie ten
goede aan de kinetische energie, maar gaat deels op aan warmte door de
luchtweerstand. De hoogte van het beginpunt zal dus in de praktijk groter
moeten zijn dan berekend is bij vraag b om bij punt B voldoende kinetische
energie over te houden.
UITW ERKINGEN OPGAVEN VW O 5 HOOFDSTUK 2
3 van 30
Opgave 6
In horizontale richting beweegt de bal over een afstand van 15 m:
sx (t )  vx  tworp 

sx  15 m
  15  40  tworp  tworp  0,375 s
vx  40 m/s 
In verticale richting valt de bal over een afstand:
2
y  12  g  tworp
 12  9,81  0,3752  0,69 m
Opgave 7
a Zie figuur 2.3.
Figuur 2.3
25 flitsen per seconde  tijd tussen twee opeenvolgende flitsen is
1
s  0, 040 s
25
Eerste manier
Tussen de eerste en de laatste stip zitten vijf tijdsintervallen.
Ieder tijdsinterval duurt 0,040 s
 vijf tijdsintervallen = 5 × 0,040 = 0,20 s
UITW ERKINGEN OPGAVEN VW O 5 HOOFDSTUK 2
4 van 30
Tweede manier
Flits  op t0 = 0,0 s
Flits  op t1 = 0,04 s
Flits  op t2 = 0,08 s
Flits  op t3 = 0,12 s
Flits  op t4 = 0,16 s
Flits  op t5 = 0,20 s
 de laatste afbeelding is gemaakt op t = 0,20 s
b In verticale richting valt de kogel over een afstand
2
sy (t )  12  g  tval
 12  9,81  0, 202  0, 20 m
c Meet in figuur 2.3 of in figuur 2.8 van het kernboek de afstand sy op.
Je vindt dan: sy = 14 hokjes.
In werkelijkheid is de afstand waarover de kogel gevallen is sy = 0,20 m
 14 hokjes in de tekening komen overeen met 20 cm in werkelijkheid
20
 1,0 hokje in de tekening komt overeen met
= 1,40 cm in werkelijkheid.
14
Meet afstand sx in figuur 2.3 of in figuur 2.8 in het kernboek op.
Je vindt dan: sx = 10 hokjes. In werkelijkheid is deze afstand
10 × 1,40 = 14 cm.
sx (t )  vx  tval 

sx  0,14 m   0,14  vx  0, 20  vx  0, 70 m/s
tval  0, 20 s 

De snelheid waarmee de kogel horizontaal is weggeschoten bedraagt 0,70 m/s.
d Eerste manier (met bewegingsvergelijkingen)
De voorlaatste opname van de kogel is gemaakt op t = 0,16 s
vx  0, 70 m/s
vy  g  tval


tval  0,16 s   vy  9,81  0,16  1,57 m/s

g  9,81 m/s 2 
2
De stelling van Pythagoras: veind
 vx2  vy2
 veind  vx2  vy2  0, 702  1,572  1, 7 m/s
Tweede manier (met de energiebalans)
Zie figuur 2.3.
Eboven in A = Ebeneden in B
Ezw,boven in A + Ekin,boven in A = Ezw,beneden in B + Ekin,beneden in B
Stel Ezw,beneden in B = 0
2
2
1
m  g  h  12  m  vboven
in A  2  m  vbeneden in B
Delen door m levert:
2
2
1
g  h  12  vboven
in A  2  vbeneden in B
vboven in A = vx = 0,70 m/s.
We moeten dus eerst het hoogteverschil Δh bepalen.
UITW ERKINGEN OPGAVEN VW O 5 HOOFDSTUK 2
5 van 30
Eerste manier
De tijd om van A naar B te gaan bedraagt 0,16 s
2
h  sy (t )  12  g  tval
 12  9,81  0,162  0,126 m
Tweede manier
In figuur 2.3 of in figuur 2.8 in het kernboek heeft Δh een lengte van 8,8 hokjes
 ∆h = 8,8 × 1,4 = 12,3 cm = 0,123 m
Nu kunnen we vx en Δh invullen:
2
2
9,81  0,126  12  0,702  12  vbeneden
in B  vbeneden in B  2,96
 vbeneden in B = 1,7 m/s
Opgave 8
a Zie figuur 2.4.
In het tijdsinterval [0 s; 0,80 s] is de beweging eenparig vertraagd, dus neemt
de verplaatsing steeds minder toe met de tijd. De (sx,t)-grafiek levert dan een
paraboolvormige grafiek op, dus een kromme grafieklijn. In het interval
[0,80 s; 1,20 s] valt het kopje van de tafel. Er werkt dan op het kopje geen
kracht meer in horizontale richting, dus is de horizontale beweging eenparig.
De horizontale verplaatsing neemt dan lineair met de tijd toe, dus is het
bijbehorende deel van de (sx,t)-grafiek een rechte lijn.
Figuur 2.4
b Zie figuur 2.4.
Bepaal de steilheid van de raaklijn op t = 0 s:
x
0, 72
vx (0)  0 
 0,90 m/s
t0 0,80
c Eerste manier
Zie figuur 2.4.
Bepaal de steilheid van de raaklijn op t = 0,80 s; de lijn in het interval
[0,80 s; 1,20 s] is recht (zie ook vraag a).
UITW ERKINGEN OPGAVEN VW O 5 HOOFDSTUK 2
6 van 30
vx (0,80) 
x0,80
t0,80

(0,84  0, 60) 0, 24

 0, 60 m/s
(1, 20  0,80) 0, 40
Tweede manier
Zie figuur 2.4  en .
De valtijd is 0,40 s (op t = 0,80 s begint de valbeweging en vanaf tval = 1,20 s
ligt het kopje op de grond); de horizontale verplaatsing tijdens de valbeweging
sx(t) = 84 – 60 = 24 cm
sx (t )  vx  tval 

sx  0, 24 m   0, 24  vx  0, 40  vx  0, 60 m/s
tval  0, 40 s 

Derde manier
s = vgem · t in het tijdsinterval [0,0 s; 0,80 s]
s  vgem  t 
s
0, 60

s  60 cm   vgem 

 0, 75 m/s
t 0,80

t  0,80 s 
v(0)  v(0,80) 
vgem 

2
0,90  v(0,80)

 vx (0,80)  0, 60 m/s
  0, 75 
v(0)  0,90 m/s
2

vgem  0, 75 m/s

d Zie figuur 2.4.
Eerste manier
v v(0,80)  v(0) (0, 60  0,90)
ax 


 0,38 m/s 2
t
0,80
(0,80)
Tweede manier
Gebruik de wet van behoud van energie in het tijdsinterval [0,0 s; 0,80 s].
De energiebalans hier is als volgt:
energiebegin = energieeind + energieonderweg
Ekin,begin = Ekin,eind + Q
2
2
1
1
2  m  vbegin  2  m  veind  Fwr  s
 m  v(0) 2  12  m  v(0,80) 2  m  ax  s
Delen door m levert:
2
2
1
1
2  v (0)  2  v (0,80)  ax  s
1
2
 12  0,902  12  0, 602  ax  0, 60  ax  0,38 m/s 2
e Zie figuur 2.4  en .
De valtijd is 0,40 s (op t = 0,80 s begint de valbeweging en vanaf t = 1,20 s ligt
het kopje op de grond); de horizontale verplaatsing tijdens de valbeweging Δsx
= 84 – 60 = 24 cm = 0,24 m
f Zie figuur 2.4.
In het tijdsinterval [0,80 s; 1,20 s] valt het kopje van de tafel op de grond. Deze
valbeweging duurt dus 1,20 – 0,80 = 0,40 s
2
h  sy (t )  12  g  tval
 12  9,81  0, 402  0,78 m
UITW ERKINGEN OPGAVEN VW O 5 HOOFDSTUK 2
7 van 30
g Eerste manier (met bewegingsvergelijkingen)
vx  0, 60 m/s
vy  g  tval


tval  0, 40 s   vy  9,81  0, 40  3,92 m/s

g  9,81 m/s 2 
2
De stelling van Pythagoras: veind
 vx2  vy2
 veind  vx2  vy2  0, 602  3,922  4, 0 m/s
Tweede manier (met de energiebalans)
Eboven (0,80 s) = Ebeneden (1,20 s)
Ezw,boven (0,80s) + Ekin,boven (0,80 s) = Ezw,beneden (1,20 s) + Ekin,beneden (1,20 s)
Stel Ezw,beneden (1,20 s) = 0
m  g  h  12  m  vx (0,80) 2  12  m  veind (1, 20) 2
Delen door m levert: g  h  12  vx (0,80) 2  12  veind (1, 20) 2
Nu kunnen we vx(0,80) en h invullen:
vx(0,80) = 0,60 m/s en h = 0,78 m
2
9,81  0, 78  12  0, 602  12  veind
 veind  4, 0 m/s
2.2
Cirkels, graden en radialen
2π
 π rad  3,14 rad
360
360
 160
b 2,80 rad  2,80 
2π
360
 57, 26
c 1, 000 rad  1, 000 
2π
Opgave 9
a 180  180 
Opgave 10
a
360
 90
2π
b Met de grafische rekenmachine TI werken we als volgt:
Controleer door middel van de toets MODE of je rekenmachine op ‘RADIAN’
of ‘Radialen’ staat. Je kunt nu – na intikken van sin( 21 ) – aflezen: 1 (exact
1,00).
Met de grafische rekenmachine CASIO werken we als volgt:
Controleer door middel van de toets SET UP of je rekenmachine op ‘Rad’
staat. Je kunt nu – na intikken van sin( 21 ) – aflezen: 1 (exact 1,00).
c Met de grafische rekenmachine TI werken we als volgt:
Controleer door middel van de toets MODE of je rekenmachine op ‘DEGREE’
of ‘Graden’ staat. Je kunt nu – na intikken van sin(90°) aflezen: 1 (exact 1,00).
1
2
π rad  12 π 
UITW ERKINGEN OPGAVEN VW O 5 HOOFDSTUK 2
8 van 30
Met de grafische rekenmachine CASIO werken we als volgt:
Controleer voor de grafische rekenmachine CASIO door middel van de toets
SET UP of je rekenmachine op ‘Deg’ staat. Je kunt nu – na intikken van
sin(90°) – aflezen: 1 (exact 1,00).
Opgave 11
Opgave 12
2π
2π
rad  150  150 
 2,62 rad
360
360
b Met de grafische rekenmachine TI werken we als volgt:
Controleer door middel van de toets MODE of je rekenmachine op ‘DEGREE’
of ‘Graden’ staat: sin(150°) = 0,500.
Met de grafische rekenmachine CASIO werken we als volgt:
Controleer voor de grafische rekenmachine CASIO door middel van de toets
SET UP of je rekenmachine op ‘Deg’ staat: sin(150°) = 0,500.
c Met de grafische rekenmachine TI werken we als volgt:
Controleer voor de grafische rekenmachine TI door middel van de toets
MODE of je rekenmachine op ‘RADIAN’ of ‘Radialen’ staat: sin(2,62
rad) = 0,498.
Met de grafische rekenmachine CASIO werken we als volgt:
Controleer voor de grafische rekenmachine CASIO door middel van de toets
SET UP of je rekenmachine op ‘Rad’ staat: sin(2,62 rad) = 0,498.
a 360  2π rad  1 
Zie figuur 2.5.
Figuur 2.5

1
π
 1 
  1'    

rad
60 180
 60 
   2,91  104 rad
0, 080
 275 m
 2,91  104
 r  0, 28 km
r
2.3
Opgave 13
s

Eenparige cirkelbeweging
Eerste manier
Toerental 1500 RPM
 φ(t) = 1500 × 2π = 9424,78 rad per minuut
 (t ) 9424, 78

 157,1 rad/s
 
t
60
Tweede manier
60
2π
2π
T
 0, 04000 s   

 157,1 rad/s
1500
T
0, 04000
UITW ERKINGEN OPGAVEN VW O 5 HOOFDSTUK 2
9 van 30
Opgave 14
180
 4,1  103 
π
b Nee. De door Desi en Josette doorlopen hoek φ(t) is even groot, maar de door
Josette afgelegde weg is groter dan die van Desi (s(t) = r ∙ φ(t), rJosette is groter
dan rDesi).
c Zie figuur 2.6.
Het snoepje krijgt op het moment van loslaten óók de baansnelheid van Desi
mee. De baansnelheid van Desi is kleiner dan die van Josette, omdat Desi
dichter bij het middelpunt zit. Daarom zal het snoepje voor Josette
‘achterblijven’.
a Doorlopen hoek:     t  0, 60  2, 0  60  72 rad  72 
Figuur 2.6
Opgave 15
a In 60 s draait de trommel 1250 keer rond.
60
Dan is T =
= 0,048 s.
1250
2π
2π
b 

 1,3  102 rad/s
T
0, 048
c De druppel doorloopt een cirkelbaan met een straal van
50
= 25 cm = 0,25 m
2
baansnelheid v = ω ∙ r = 1,3 ∙ 102 × 0,25 = 33 m/s
of
2π  r 2π  0,25
baansnelheid v 

 33 m/s
T
0, 048
Opgave 16
a Bandlengte l = v ∙ t = 5,00 ∙ 10–2 × 45,0 × 60 = 135 m
UITW ERKINGEN OPGAVEN VW O 5 HOOFDSTUK 2
10 van 30
b De grootste hoeksnelheid heb je bij de kleinste straal:
2, 20
5,00  102
rmin 
 1,10 cm  max 
 4,55 rad/s
2
1,10  102
De kleinste hoeksnelheid heb je bij de grootste straal:
4,80
5,00  102
rmax 
 2, 40 cm  min 
 2,08 rad/s
2
2, 40  102
c Bij het begin: t = 0 min  ω0 = ωmax = 4,55 rad/s
Bij het eind: t = 45 min  ω45 = ωmin = 2,08 rad/s
halverwege: t = 22,5 min
2, 40  1,10
5,00  102
r22,5 
 1,75 cm  22,5 
 2,86 rad/s
2
1,75  102
Het diagram vind je in figuur 2.7.
Figuur 2.7
Opgave 17
a Zie figuur 2.8 voor wat bedoeld wordt met de straal r.
Meet de straal r op in figuur 2.15 van het kernboek: rfiguur = 2,7 cm
 in werkelijkheid is r = 10 × 2,7 = 27 cm = 0,27 m
Figuur 2.8
UITW ERKINGEN OPGAVEN VW O 5 HOOFDSTUK 2
11 van 30
b De stroboscoop gaf 25 flitsen per seconde
 de tijd tussen twee flitsen = 251 s = 0,040 s.
Zie figuur 2.8 voor wat bedoeld wordt met middelpuntshoek α.
Beschouw de eerste en de elfde afbeelding van de puck.
Meet in figuur 2.15 van het kernboek de bijbehorende middelpuntshoek α op
287
β = 73°  α = 360 – 73 = 287° =
× 2π = 5,01 rad
360
Deze hoek is in 10 × 0,040 s = 0,40 s afgelegd.
Er geldt immers:
tijd tussen puck (1) en puck (2) = 251 s = 0,04 s
tijd tussen puck (1) en puck (3) = 2 × 251 s = 0,08 s
tijd tussen puck (1) en puck (11) = 10 × 251 s = 0,40 s
Eerste manier
 (t ) 5, 01


 13 rad/s
t
0, 40
Opgave 18
Tweede manier
Een draaiing over 360° vindt dan plaats in:
360
× 0,40 = 0,502 s  T = 0,502 s
287
2π
2π


 13 rad/s
T
0,502
c Baansnelheid v = ω · r = 13 × 0,27 = 3,5 m/s
of
2π  r 2π  0,27
baansnelheid v 

 3, 4 m/s
T
0,502
a Zie figuur 2.9.
Figuur 2.9
rK: straal van de cirkelbaan van Kampala
rP: straal van de cirkelbaan van Sint-Petersburg
KMKP = 60°  PMKMP = 30°
PM P
In ∆PMKMP: sin 30° =
PM K
UITW ERKINGEN OPGAVEN VW O 5 HOOFDSTUK 2
12 van 30
PMP = rP en PMK = KMK = raarde = rK
r
r
1
2
sin 30  P  rP  rK  sin 30  0,5  rK  K 

rK
rP 0,5 1
 2π 
2π 


b hoeksnelheid  
K  Taarde  1



T 
P  2π  1

TK  TP  Taarde



 Taarde 
c baansnelheid v    r 
vK K  rK rK 2

rK  2  rP




vP P  rP
rP 1

K  P

Opgave 19
a Zie figuur 2.10.
Alle schakels van de ketting hebben dezelfde snelheid, dus de tanden op beide
tandwielen hebben dezelfde snelheid. De baansnelheid van de tanden op I is
dus even groot als de baansnelheid van de tanden op II.
Figuur 2.10
b De baansnelheden van beide tandwielen zijn gelijk
v
baansnelheid v    r 
 

I  rI  rII 1
v

 




r
II  v  rI 2

 
rI  2  rII

 rII 
 2π 
 
TI  I  II 2
2π
2π 
c hoeksnelheid  
T 




T
  TII  2π  I 1


 II 
2.4
Opgave 20
a
b
c
d
e
Middelpuntzoekende kracht en middelpuntzoekende
versnelling
De vereiste middelpuntzoekende kracht is in alle gevallen de resulterende
kracht op de draaiende voorwerpen.
De elektrische kracht tussen de positief geladen atoomkern en het negatief
geladen elektron.
De gravitatiekracht tussen de aarde en de maan.
De normaalkracht van de trommelwand op het wasgoed.
De dwarswrijvingskrachten tussen de banden en het wegdek.
De horizontaal gerichte resultante van de spankracht en de zwaartekracht.
UITW ERKINGEN OPGAVEN VW O 5 HOOFDSTUK 2
13 van 30
Opgave 21
a Zie BINAS tabel 31 Planetenstelsel.
De (gemiddelde) afstand van de maan tot de aarde: raarde–maan = 384,4 ∙ 106 m
De omlooptijd van de maan om de aarde
Tmaan = 27,32 d(ag) = 27,32 × 24 × 3600 = 2,360 ∙ 106 s
Massa van de maan: mmaan = 0,0735 ∙ 1024 kg
b De baansnelheid is
2π  rmaan 2π  384, 4  106
vmaan 

 1, 023  103 m/s ( 1,023 km/s)
3
Tmaan
2,360  10
c De gravitatiekracht levert de benodigde middelpuntzoekende kracht:
m
 v2
0, 0735  1024  10232
Fmpz  maan maan 
raarde-maan
384, 4  106
 Fmpz = 2,00 ∙ 1020 N
 Fgrav = 2,00 ∙ 1020 N
Opgave 22
a Zie figuur 2.11.

Er werken twee krachten op het blokje: de zwaartekracht F zw en de spankracht

F span .
Figuur 2.11
b De resultante van de zwaartekracht en de spankracht:


F res  F mpz




F zw  F span  F res  F mpz

Hierbij is F mpz gericht van A naar M.
c Zie figuur 2.11.
In ∆ABC geldt: tan  
AB Fmpz

AC Fzw
 m  v2 
mv 


r 
Fmpz 
m  v2
v2




r   tan  
m  g  m  g  r g  r
Fzw  m  g 

2
UITW ERKINGEN OPGAVEN VW O 5 HOOFDSTUK 2
14 van 30
d De snelheid v waarmee het blokje ronddraait, volgt direct uit de bij vraag c
afgeleide relatie.
v2 = g ∙ r ∙ tan α  v  g  r  tan 
Bepaling r:
AM r

In ∆AMD geldt: sin  
AD l
 r  l  sin   0,75  sin 35  0, 43 m
 v  g  r  tan 
 v  9,81  0, 43  tan 35  1, 7 m/s
e Zie figuur 2.12.
Direct nadat het touwtje gebroken is, heeft het blokje slechts een horizontale
snelheid. Er werkt nu op het blokje alleen nog de zwaartekracht. De beweging
van het blokje is die van een horizontale worp.
Figuur 2.12
Figuur 2.13
f Zie figuur 2.12.
Eerste manier (met de energiebalans)
Eboven in A = Ebeneden in B
Ezw,boven in A + Ekin,boven in A = Ezw,beneden in B + Ekin,beneden in B
Stel Ezw,beneden in B = 0
2
2
1
m  g  hA  12  m  vboven
in A  2  m  vbeneden in B
UITW ERKINGEN OPGAVEN VW O 5 HOOFDSTUK 2
15 van 30
2
2
1
Delen door m levert: g  h  12  vboven
in A  2  vbeneden in B
vboven in A = 2,5 m/s; hA = 125 cm = 1,25 m
2
 9,81  1, 25  12  2,52  12  vbeneden
in B
 vbeneden in B  5,5 m/s
Tweede manier (met bewegingsvergelijkingen)
Zie figuur 2.13.
2

hA  12  g  tval

2
hA  1, 25 m   1, 25  12  9,81  tval
 tval  0,5048 s

g  9,81 m/s 2 
vx  2,5 m/s
vy  g  tval


tval  0,5048 s   vy  9,81  0,5048  4,95 m/s

g  9,81 m/s 2 
De stelling van Pythagoras: vB2  vx2  vy2
 vB  vx2  vy2  2,52  4,952  5,5 m/s
Opgave 23
2π
2π
2π


 7,3  105 rad/s
T
1 dag 24  60  60
b Zie BINAS tabel 31: Planetenstelsel.
De straal van de aarde (equator = evenaar): raarde = 6,378 · 106 m
a aarde 
Eerste manier
ampz   2  r  (7,3  105 )2  6,378  106  0,034 m/s2
Tweede manier

v2
ampz 

r

5
6
v    r  7,3  10  6,378  10  466 m/s 

4662
 0, 034 m/s2
6
6,378  10
c v    r  7,3  105  6,378  106  4,7  102 m/s
d Baansnelheid v = ω ∙ r = 0,0 m/s, want r = 0,0 m.
De hoeksnelheid is voor alle punten op aarde 7,3 ∙ 10–5 rad/s; dus ook voor een
punt op de Noordpool.
Middelpuntzoekende versnelling ampz = ω2 ∙ r = 0,0 m/s2, want r = 0,0 m.
 ampz 
2.5
Opgave 24
Toepassingen
a De hoogte van de auto verandert niet, dus de auto maakt een bocht in het
horizontale vlak. De vereiste middelpuntzoekende kracht ligt dus ook in het
horizontale vlak.
UITW ERKINGEN OPGAVEN VW O 5 HOOFDSTUK 2
16 van 30
b Zie figuur 2.14.
Figuur 2.14

c De middelpuntzoekende kracht ( F mpz ) wordt geleverd door de resultante van

de normaalkracht op de wielen van de auto door het wegdek ( F n ) en de

zwaartekracht ( F zw ). Dat is dus de horizontale component van de

normaalkracht ( F n,x ).
m  v 2 1, 2  103  252
d Fn,x  Fmpz 

 1,00  103 N
3
r
0,75  10
Fn,y  Fzw  m  g  1, 2  103  9,81  1,18  104 N
In ∆ABZ geldt:
AB Fn,x 1, 00  103
tan  


 0, 08475
AZ Fn,y 1,18  104
   4,8
Opgave 25
a Zie figuur 2.15.
In het uiterste punt A bezit Petra alleen zwaarte-energie. Bij de beweging van
A naar B wordt de zwaarte-energie omgezet in bewegingsenergie.
De energiebalans is dus: Ezw,A = Ekin,B
Ezw,A  m  g  h  50  9,81  4, 0  1962 J
 Ekin,B  1962 J 

Ekin  12  m  v 2 
2
1
2  m  vB  1962
1
2
 50  vB2  1962
 vB  8,9 m/s
UITW ERKINGEN OPGAVEN VW O 5 HOOFDSTUK 2
17 van 30
Figuur 2.15
v 2 8,92

 13 m/s2
r
6,0
c De grootte van de spierkracht ( F
b ampz 
spier
grootte van de spankracht ( F
span
) die Petra moet leveren is gelijk aan de
) in het touw.
Als Petra in een cirkelbeweging door het laagste punt gaat, moet de grootte van
de spankracht ( F ) gelijk zijn aan de grootte van de zwaartekracht ( F ) +
span
zw
de grootte van de middelpuntzoekende kracht ( F
mpz
).

m  v2
 m  ampz  50  13  650 N 
r


 m  g  50  9,81  491 N

Fmpz 
Fzw
 Fspier  Fspan  Fmpz  Fzw  650  491  1,1  103 N
Opgave 26
a Eerste manier
De emmer heeft een inhoud van 10 liter en is voor 40% gevuld met water
 er zit 4,0 liter water in de emmer
4,0 liter water heeft een massa van 4,0 kg
(m = ρ ∙ V = 0,998 ∙ 103 × 4,0 ∙ 10–3 = 4,0 kg)
 Fzw = 4,0 × 9,81 = 39,2 N
m  v 2 4,0  102
Fmpz 

 5,0  102 N
r
0,80
Fmpz > Fzw, dus blijft het water in de emmer.
Tweede manier
Het water zal in het hoogste punt net niet omlaag vallen als de normaalkracht
m  v2
 m  g  vmin  r  g
nul is. Dan geldt: Fmpz = Fzw, dus
r
vmin  r  g  0,80  9,81  2,8 m/s; je draait de emmer rond met een
snelheid v van 10 m/s
 v > vmin  het water blijft in de emmer.
UITW ERKINGEN OPGAVEN VW O 5 HOOFDSTUK 2
18 van 30

b De middelpuntzoekende kracht ( F mpz ) op het water is de resulterende kracht



( F res ) van de zwaartekracht ( F zw ) op het water en de normaalkracht ( Fn ) die
de bodem van de emmer op het water uitoefent.
Fres  Fmpz  Fzw  Fn 

m  v2

Fmpz 
 500 N   500  39, 2  Fn  Fn = 4, 6  10 2 N
r

Fzw  m  g  39, 2 N 
Opgave 27
a Zie figuur 2.16.


De middelpuntzoekende kracht ( F mpz ) op jou is de resulterende kracht ( F res )


van de zwaartekracht ( F zw ) op jou en de normaalkracht ( Fn ) die de bodem
van de bank op je uitoefent.
In A kom je net los van de bank: Fn = 0 N
Fmpz  Fzw 

m  v2 
m  v2
v2
Fmpz 
 mg 
 g  v2  g  r

r 
r
r
Fzw  m  g 
v  g  r  9,81  3,00  5, 42 m/s
Figuur 2.16
b Zie figuur 2.16 (punt A).


De zwaartekracht ( F zw ) en de middelpuntzoekende kracht ( F mpz ) zijn beide

naar beneden gericht, de normaalkracht ( Fn ) die de bank op je uitoefent is
naar boven gericht:
Fres  Fmpz  Fzw  Fn


2
2
mv
56, 0  5, 00

Fmpz 

 466, 7 N   466, 7  549, 4  Fn  Fn  82, 7 N
r
3, 00


Fzw  m  g  56, 0  9,81  549, 4 N
UITW ERKINGEN OPGAVEN VW O 5 HOOFDSTUK 2
19 van 30
c Zie figuur 2.16 (punt B).


De zwaartekracht ( F zw ) is naar beneden gericht; de normaalkracht ( Fn ) die de

bank op je uitoefent en de middelpuntzoekende kracht ( F mpz ) zijn beide naar
boven gericht:
Fres  Fmpz  Fn  Fzw


m  v2

Fmpz 
 466, 7 N   466, 7  Fn  549, 4  Fn  1, 02  103 N
r

Fzw  m  g  549, 4 N 
Opgave 28
a Zie figuur 2.17.
Het wagentje zal in het hoogste punt net niet omlaag vallen als de
normaalkracht nul is. Dan geldt:
m  v2
Fmpz  Fzw , dus
 m g
r
2
 vmin
 r  g  vmin  r  g
Figuur 2.17
b Zie figuur 2.17.
De energiebalans: E in A = E in L
Ezw,A = Ezw, L + Ekin, L
Stel Ezw,beneden in B = 0
m  g  hA  m  g  hL  12  m  vL2
Delen door m levert: g  hA  g  hL  12  vL2
hL = 2 · r; vL  r  g (zie vraag a).
Dit invullen levert:
g  hA  g  (2  r )  12  ( r  g ) 2
 g  hA  2  r  g  12  r  g  2 12  r  g
Delen door g levert:
hA  2 12  r  52  r
Opgave 29
a Zie figuur 2.18.
Op de kogel werken twee krachten:
Fzw  mkogel  g  6, 25  9,81  61,31 N
Fspan = Fspier = 2,80 kN = 2,80 · 103 N
UITW ERKINGEN OPGAVEN VW O 5 HOOFDSTUK 2
20 van 30
De resultante van deze twee krachten levert de vereiste horizontaal gerichte

middelpuntzoekende kracht ( F mpz ).
In ΔABC geldt:
F
BC
61,31
cos  
 zw 
 0, 0219
AC Fspan 2,80  103
   88, 7
Figuur 2.18
b Zie figuur 2.18.
De baansnelheid volgt uit de middelpuntzoekende kracht: Fmpz
m  v2

r
In ΔABC geldt het volgende.
Eerste manier
AB Fmpz
sin  

AC Fspan
 Fmpz  Fspan  sin   2,80  103  sin88,7  2799 N
Tweede manier
De stelling van Pythagoras: AB2 + BC2 = AC2
2
2
2
2
 Fmpz
 Fzw2  Fspan
 Fmpz
 Fspan
 Fzw2
2
 Fmpz  Fspan
 Fzw2  (2,80  103 ) 2  61,312  2799 N
m  v2
6, 25  v 2
 2799 
r
1,85
2
 v  828,5  v  28,8 m/s
c Met bewegingsvergelijkingen:
2

h  12  g  tval

2
h  1,55 m   1,55  12  9,81  tval
g  9,81 m/s 2 
 tval  0,5621 s
Fmpz 
x  vx  tval


vx  28,8 m/s   x  28,8  0,5621  16, 2 m
tval  0,5621 s 

UITW ERKINGEN OPGAVEN VW O 5 HOOFDSTUK 2
21 van 30
d Yuriy Sedykh werpt de kogel schuin omhoog weg, waardoor de kogel veel
verder komt.
2.6
Opgave 30
a Fgrav
Gravitatiekracht
Fgrav  r 2
m1  m2
G
G 
r2
m1  m2
eenheid van G:
eenheid van Fgrav :
eenheid van r:
eenheid van m:

[ Fgrav ]  N 

[r ]
m
[m]  kg 
[G ]
N  m2
 N·m2 ·kg 2
kg 2
b Fgrav  m1  g


m1  m2 
Fgrav  G 
r 2 
m m
 m1  g  G  1 2 2
r
m
 g  G  22
r
eenheid van g: [ g ]

2
2 
eenheid van G: [G ]  N  m  kg 

eenheid van r: [r ]  m


eenheid van m: [m]  kg
kg
  g   (N·m 2 ·kg 2 )  2  N  kg 1
m
2
1 N  1 kg  m  s
 G  
  g   (kg  m  s 2 )  kg 1  m  s 2
Opgave 31
a massa = dichtheid × volume (m = ρ ∙ V)
De dichtheid van lood: ρPb = 11,3 ∙ 103 kgm–3 (zie BINAS tabel 8 Gegevens van
metalen).
4
Het volume van een bol: Vbol   π  r 3
3
Bol 1  diameter 5,0 cm  straal r1 = 2,5 cm = 2,5 ∙ 10–2 m
4
4
Het volume van bol 1: Vbol,1   π  r 3  π  (2,5  102 )3  6,54  105 m3
3
3
 de massa van bol 1 is mbol,1 = ρPb ∙ Vbol,1 = 11,3 ∙ 103 × 6,54 ∙ 10–5 = 0,74 kg
Bol 2  diameter 30,0 cm
 straal r2 = 15,0 cm = 15,0 ∙ 102 m
4
4
Het volume van bol 2: Vbol,1   π  r 3  π  (15,0  102 )3  1, 414  102 m3
3
3
 de massa van bol 2 is mbol,2 = ρPb ∙ Vbol,2 = 11,3 ∙ 103 × 1,414 ∙ 10–2 = 160 kg
UITW ERKINGEN OPGAVEN VW O 5 HOOFDSTUK 2
22 van 30
mbol,1  mbol,2


r

G  6, 6726  1011 N  m 2  kg 2 

mbol,1  0, 74 kg


mbol,2  160 kg

r  45, 0 cm  0,450 m

0, 74  160
 Fgrav  6, 6726  1011 
 3,9  108 N
0, 4502
b Fgrav  G 
Opgave 32
2
a Zie BINAS tabel 31 Planetenstelsel.
De massa van de aarde: maarde = 5,976 ∙ 1024 kg
gemiddelde afstand tot de zon raarde-zon = 0,1496 ∙ 1012 m
Zie BINAS tabel 32C Gegevens over sterren.
De massa van de zon mzon = 1,989 ∙ 1030 kg
m
m
Fgrav  G  aarde zon
(raarde-zon ) 2
Fgrav  6,6726  1011 
5,976  1024  1,989  1030
(0,1496  1012 ) 2
Fgrav  3,544  1022 N
b Er is sprake van een wisselwerking tussen de massa’s. Ze oefenen een kracht
op elkaar uit. De kracht van de aarde op de zon is dus ook 3,544 ∙ 1022 N.
Opgave 33
a m1  m2  m


r1 4


r2 1


m  M aarde 
Fgrav  G 

r2
m M
1
G  1 2 aarde
2
2
Fgrav,1
r1
r12 r22  r2 
1
1



 2     
m

M
1
Fgrav,2 G  2
r1
16
4
aarde
 r1 
2
2
r2
r2
b
r1 4

r2 1
De 3e wet van Kepler:
r 3 G M aarde

T2
4π 2



 constant 

 r13
r23

T 2 T 2
2
 1
3
3
 2
r13  r1   4 
64
 T1
 2  3     
r2  r2   1 
1
 T2
 T
8
 1 
 T2 1
UITW ERKINGEN OPGAVEN VW O 5 HOOFDSTUK 2
23 van 30
2πr
T 

4



1


8


1

c v
r1
r2
T1
T2
 2  π  r1   r1 

  
v1  T1   T1   r1   T2 



   
v2  2  π  r2   r2   T1   r2 

  
 T2   T2 
v
T r 1 4 1
 1  2 1   
v2 T1 r2 8 1 2
Opgave 34
a Zie figuur 2.19.
Maak een tekening op schaal.
Laat in je tekening één schaaldeel overeenkomen met 2000 km.
Teken een cirkel (= de aarde) met een straal 3,2 schaaldeel
6378
(straal aarde = 6400 km  in tekening is dit
= 3,2 schaaldeel)
2000
M = middelpunt van de aarde
E = evenaar
S = satelliet
Teken de lijn MES; maak ES 18 schaaldelen lang
(de satelliet S staat 36.000 km van de aarde af  in de tekening is dit
36 000
= 18 schaaldelen)
2000
Utrecht ligt op 52° noorderbreedte
 maak α 52° en je vindt nu het punt U (= Utrecht).
Verbind het punt S met het punt U.
Teken nu in het punt U de raaklijn (= horizon in Utrecht) aan de cirkel.
Meet hoek MUS = 121°  de hoek van de schotelantenne met de horizon
(β) = 31°
Figuur 2.19
UITW ERKINGEN OPGAVEN VW O 5 HOOFDSTUK 2
24 van 30
b Zie figuur 2.19.
Teken loodlijn UL.
In ΔMLU:
LU
sin  
MU
 LU  MU  sin   6378  sin52  5026 km
LM
cos  
MU
 LM  MU  cos   6378  cos52  3927 km
In ΔSLU:
LS = MS – LM = 36 000 + 6378 – 3927 = 38 451 km
LU
5026
tan  

 0,13071    7, 45
LS 38 451
In ΔSMU:
hoek γ = 7,45° en hoek α = 52°  hoek SUM = 180° – 7,45° – 52° = 120,6°
 de hoek van de schotelantenne met de horizon (β) = 120,6° – 90° = 31°
c De baan is geostationair, want de satelliet bevindt zich op een vaste plaats
boven de evenaar.
d Drie verschillen tussen een geostationaire en een polaire satelliet zijn als volgt:
1 Een geostationaire satelliet bevindt zich boven de evenaar en een polaire
satelliet beschrijft een baan over de polen van de aarde.
2 Een geostationaire satelliet heeft een omlooptijd van 24 uur en een polaire
satelliet heeft dit niet.
3 Alle geostationaire satellieten bevinden zich op dezelfde afstand van het
aardoppervlak en hebben een vaste plaats; polaire satellieten hebben dit niet.
Opgave 35
a De omlooptijd van de satelliet is gelijk aan de omwentelingstijd van de aarde,
dus 24 uur.
b In BINAS tabel 31 vind je dat de siderische rotatieperiode van de aarde 23,93 h
is. De (siderische) omlooptijd voor de geostationaire satelliet is dan ook
23,93 uur.
De siderische omwentelingstijd van de aarde is de echte omwentelingstijd. Bij
de omwentelingstijd zoals wij die op aarde ervaren, houden we geen rekening
met de invloed die de tussentijdse verplaatsing langs de baan om de zon heeft
op onze waarneming.
c Noem de straal van de satellietbaan r en de massa van de satelliet msat.
Voor de satelliet wordt de middelpuntzoekende kracht geleverd door de
zwaartekracht: Fmpz = Fgrav.
2
msat  v 2
msat  M aarde
2πr 

G



r
r2

m  v2
 T   G  M aarde
Fmpz  sat

M aarde
v2
r
r2
r


G



r
r2
msat  M aarde 
 4  π2  r 2 
Fgrav  G 


2
2πr

r2
 T
  G  M aarde
v
T
r
r2
M
r3
 2  G  aarde2  constant
T
4π
Dit is de derde wet van Kepler, die we hebben afgeleid onder de aanname dat
planeetbanen cirkelvormig zijn.
UITW ERKINGEN OPGAVEN VW O 5 HOOFDSTUK 2
25 van 30
In het geval dat voorwerpen in cirkelvormige banen om de aarde draaien
r 3 G M aarde
(bijvoorbeeld satellieten of de maan), geldt: 2 
 constant (zie
T
4π 2
kernboek)
G M aarde 2

r3 
T
2

4π

T  23,93 h  23,93  3600  86 148 s 

G  6, 6726  1011 N  m 2  kg 2

M aarde  5,976  1024 kg

11
24
6, 6726  10  5,976  10
 r3 
 86 1482
2
4π
3
22
 r  7, 4961  10
 r  4, 216  107 m  4, 216  10 4 km
De straal van de aarde is (zie BINAS tabel 31): 6,378106 m, dus 6378 km.
De hoogte van de satelliet h boven de evenaar is dus:
h = r – Raarde = 4,216 ∙ 104 km – 6378 km = 3,58 ∙ 104 km
d We zien dat de massa van de satelliet niet van belang is voor de berekening.
Dat is te begrijpen, want de gravitatiekracht tussen de nieuwe satelliet is
weliswaar twee keer zo groot, maar de vereiste middelpuntzoekende kracht
ook. De hoogte van een twee keer zo zware satelliet is dus ook 3,58 ∙ 104 km
Een andere oplossing gaat als volgt.
In vraag c staat een formule voor de derde wet van Kepler. In die formule,
r 3 G M aarde

 constant, komt de massa van de satelliet (msat) niet meer voor.
T2
4π 2
De straal r van zijn cirkelbeweging om de aarde is dus onafhankelijk van de
massa van de satelliet. Voor een twee keer zo zware satelliet geldt dus, dat zijn
hoogte boven het aardoppervlak gelijk is aan die van vraag b.
Dus: h = 3,58 ∙ 104 km.
Opgave 36
Voor satelliet 1 geldt:
h1 = 300 km = 3,00 ∙ 105 m
 rsat,1 = raarde + h1 = 6,378 ∙ 106 + 0,300 ∙ 106 m = 6,678 ∙ 106 m
Voor satelliet 2 geldt:
h2 = 1000 km = 1,000 ∙ 106 m
 rsat,2 = raarde + h2 = 6,378 ∙ 106 + 1,000 ∙ 106 m = 7,378 ∙ 106 m
Eerste manier
Fmpz  Fgrav


2
msat  v

Fmpz 

r

msat  M aarde 
Fgrav  G 

r2
UITW ERKINGEN OPGAVEN VW O 5 HOOFDSTUK 2
26 van 30
msat  v 2
m M
 G  sat 2 aarde
r
r
2
 v  G  M aarde
r
r2
M
v 2  G  aarde
r
M
 v  G  aarde
r
M
vsat,1  G  aarde
rsat,1
 vsat,1  6, 6726  1011 
vsat,1 
Tsat,1 
5,976  1024
 7, 7273  103 m/s
6
6,678  10
2  π  rsat,1
Tsat,1
2  π  rsat,1
vsat,1

2  π  6,678  106
7, 7273  103
Tsat,1  5430 s  90,50 min
M aarde
rsat,2
 vsat,2  G 
 vsat,2  6, 6726  10
vsat,2 
5,976  1024

 7,3516  103 m/s
6
7,378  10
11
2  π  rsat,2
Tsat,2
 Tsat,2 
2  π  rsat,2
vsat,2
2  π  7,378  106

 6306 s = 105,1 min
7,3516  103
Tweede manier
r 3 G M aarde

 constant
T2
4π 2
6, 6726  10 11  5,976  10 24

 1, 0101  1013
4π 2
De derde wet van Kepler:
r 3 G M aarde

T2
4π 2
3
rsat,1
 1, 0101  1013
2
sat,1
T
T
2
sat,1

3
rsat,1
1, 0101  1013

(6, 678  106 )3
 2,9483  107
1, 0101  1013
 Tsat,1  2,9483  107  5430 s  90,50 min
UITW ERKINGEN OPGAVEN VW O 5 HOOFDSTUK 2
27 van 30
3
rsat,2
 1, 0101  1013
2
Tsat,2
T
2
sat,2

3
rsat,2
1, 0101  1013

(7,378  106 )3
 3,9760  107
1, 0101  1013
 Tsat,2  3,9760  107  6305 s  105,1 min
Opgave 37
a Eerste manier
Fmpz  Fgrav


msat  v

Fmpz 
 msat  v 2
m M
 G  sat 2 aarde
raarde

raarde
raarde

msat  M aarde 
Fgrav  G 
2

raarde
2
M
M
v

 G  2aarde  v 2  G  aarde
raarde
raarde
raarde
2
v  G
M aarde
5,976  1024
 6, 6726  1011 
raarde
6,378  106
 v  7,907  103 m/s
2  π  raarde

v

T

3
v  7,907  10 m/s 
T 
2  π  raarde 2  π  6,378  106

 5068 s  84,47 min
v
7,907  103
Tweede manier
r 3 G M aarde

 constant
T2
4π 2
3
4π 2  raarde
2
T 
G M aarde
De derde wet van Kepler:
3
raarde
G M aarde

2
T
4π 2
T 
3
4π 2  raarde
G M aarde
4π 2  (6,378  106 )3
 5068 s  84,47 min
6, 6726  1011  5,976  1024
b Beschouw de aarde als een homogene, vaste bol. De steen wordt in het eerste
gedeelte van zijn reis tot aan het middelpunt van de aarde versneld door de
aantrekkingskracht van een gedeelte van de massa van de aarde. Maar in het
tweede gedeelte zorgt precies dezelfde hoeveelheid massa voor een even grote
vertraging van de steen. De steen komt dus precies met snelheid 0 aan de
andere kant van de aarde aan de oppervlakte. Dit houdt tevens in dat de steen
aan de andere kant van de aarde dus niet uit het gat komt.
c Ook 84,47 min.
T 
UITW ERKINGEN OPGAVEN VW O 5 HOOFDSTUK 2
28 van 30
Opgave 38
a Zie figuur 2.20.
De straal van de baan van maan I: rI = 100 ∙ 107 m; de omlooptijd van maan I:
TI = 7,0 dag
De straal van de baan van maan II: rII = 64 ∙ 107 m; de omlooptijd van maan II:
TII = 3,6 dag
r13
(100  107 )3

T12 (7, 0  24  3600)2
r13 1, 00  1027

T12 3, 66  1011
r13
 2, 7  1015 m3s 2
2
T1
r23
(64  107 )3

T22 (3, 6  24  3600) 2
r23 2, 62  1026

T22 9, 67  1010
r23
 2, 7  1015 m3s 2
2
T2

r13
r23

 constant
T12 T22
Figuur 2.20
UITW ERKINGEN OPGAVEN VW O 5 HOOFDSTUK 2
29 van 30
b vI 
2  π  rI
TI
rI  100  107 m
TI  7, 0 dag
TI  7, 0  24  3600  6, 048  103 s
2  π  100  107
vI 
 1, 0  104 m/s
3
6, 048  10
c Zie figuur 2.20 (1).
De manen bevinden zich op een lijn als hun afstanden tot de planeet gelijk zijn.
Dit gebeurt na t = 0 voor het eerst op t = 0,88 dagen.
d Zie figuur 2.21.
Noem de afstand van de aarde tot de planeet d. Rond het tijdstip t = 0,5 dag
bevindt maan II zich achter de planeet. Dus tussen t = 0 en t = 1,2 dag is de
afstand tussen de aarde en maan II groter dan d. Rond het tijdstip t = 1,5 dag
bevindt maan I zich voor de planeet. Dus tussen t = 0 en t = 3,2 dag is de
afstand tussen de aarde en maan I kleiner dan d. Dan staat maan I op t = 0,88
dagen dus dichter bij de aarde dan maan II.
Figuur 2.21
UITW ERKINGEN OPGAVEN VW O 5 HOOFDSTUK 2
30 van 30