Pulsar 3e editie natuurkunde 4 vwo uitwerkingen

Hoofdstuk 1 Gedrag
Pulsar
3e editie
natuurkunde
4 vwo
uitwerkingen
242759_NAT 3E TF HAVO 4 UW_FM.indd 1
15/07/13 12:30 PM
Hoofdstuk 1 Gedrag
Serieoverzicht Pulsar
Delen voor
bovenbouw
vmbo
Delen voor
onderbouw
vmbo
Natuurkunde
6 vwo
Natuurkunde
5 havo
Natuurkunde
5 vwo
Natuurkunde
4 havo
Natuurkunde
4 vwo
Natuurkunde
3 havo
Natuurkunde
3 vwo
Nask hv 1-2
Vormgeving binnenwerk: Ebel Kuipers, Sappemeer
Vormgeving omslag: G2K Designers, Groningen / Amsterdam
Technische tekeningen: Integra Software Services, Pvt.Ltd., India
Deze uitgave is gedrukt op FSC-papier.
0 / 13
© 2013 Noordhoff Uitgevers bv, Groningen/Houten, The Netherlands
Behoudens de in of krachtens de Auteurswet van 1912 gestelde uitzonderingen mag niets uit deze uitgave worden
verveelvoudigd, opgeslagen in een geautomatiseerd gegevensbestand of openbaar gemaakt, in enige vorm of op enige
wijze, hetzij elektronisch, mechanisch, door fotokopieën, opnamen of enige andere manier, zonder voorafgaande
schriftelijke toestemming van de uitgever. Voor zover het maken van reprografische verveelvoudigingen uit deze uitgave
is toegestaan op grond van artikel 16h Auteurswet 1912 dient men de daarvoor verschuldigde vergoedingen te voldoen
aan Stichting Reprorecht (Postbus 3060, 2130 KB Hoofddorp, www.reprorecht.nl). Voor het overnemen van (een)
gedeelte(n) uit deze uitgave in bloemlezingen, readers en andere compilatiewerken (artikel 16 Auteurswet 1912) kan men
zich wenden tot Stichting PRO (Stichting Publicatie- en Reproductierechten Organisatie, Postbus 3060, 2130 KB
Hoofddorp, www.stichting-pro.nl).
All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form
or by any means, electronic, mechanical, photocopying, recording or otherwise without prior written permission of the
publisher.
ISBN 978-90-01-81108-2
242759_NAT 3E TF HAVO 4 UW_FM.indd 2
15/07/13 12:30 PM
Pulsar
3e editie
natuurkunde
4 vwo
uitwerkingen
Auteurs
Leo te Brinke
Ton van den Broeck
Sjef Buil
Dick Hoekzema
Gerben de Jong
Joost Massolt
René van der Veen
Jos Verbeek
Paul Zuurbier
Eindredactie
Sjef Buil
Lieke Heimel
Peter Koopmans
Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_FM.indd 3
15/07/13 12:30 PM
242759_NAT 3E TF HAVO 4 UW_FM.indd 4
15/07/13 12:30 PM
Hoofdstuk 1 Gedrag
Inhoud
1
1.1
1.2
1.3
1.4
2
2.1
2.2
2.3
2.4
2.5
3
3.1
3.2
3.3
3.4
3.5
4
4.1
4.2
4.3
4.4
Bewegen in grafieken 6
Introductie 6
Snelheid meten 6
Plaatsgrafieken 8
Snelheidsgrafieken 9
Bewegen in modellen 11
Toepassing 13
Proefwerkopgaven 14
5
5.1
5.2
5.3
5.4
5.5
5.6
Bewegen en rekenen 16
Introductie 16
Snelheid 16
Versnellen 18
Vallen 20
Videometen 22
Nauwkeurig meten en rekenen 23
Toepassing 25
Proefwerkopgaven 29
Elektriciteit 30
Introductie 30
Lading spanning en stroom 30
Weerstand 31
Serie en parallel 32
Elektrische energie 35
Elektriciteit veilig in huis 36
Toepassing 37
Proefwerkopgaven 39
6
6.1
6.2
6.3
6.4
7
7.1
7.2
7.3
7.4
Eigenschappen van stoffen 52
Introductie 52
Het deeltjesmodel 52
Uitzetting 53
Stroming, geleiding en straling 55
Warmte uitwisseling 56
Eigenschappen van gassen 57
Optische eigenschappen van stoffen 59
Toepassing 60
Proefwerkopgaven 63
Kracht als vector 64
Introductie 64
Krachten zijn vectoren 64
Krachten onder een hoek 65
Rekenen met krachten als vectoren 66
Krachten op een helling 67
Toepassing 69
Proefwerkopgaven 71
Energie Omzetten 72
Introductie 72
Energiesoorten 72
Optrekken en afremmen 74
Meer arbeid 76
Zuinig met energie 78
Toepassing 79
Proefwerkopgaven 81
Kracht en beweging 40
Introductie 40
Weerstand en beweging 40
Kracht en versnellling 41
Zwaartekracht en massa 43
Wisselwerking van krachten 45
Toepassing 47
Proefwerkopgaven 50
© Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_FM.indd 5
15/07/13 5:54 PM
Hoofdstuk 1 Bewegen in grafieken
Hoofdstuk 1
Bewegen in grafieken
1
Introductie
9,93 s
Aflezen bij de vijfde verticale groene lijn vanaf rechts.
2
Op het moment van de foto is alleen de eerste over
de finish. De anderen kunnen elkaar nog inhalen.
3
C
4
Ja, stilstaande voorwerpen komen zeer uitgerekt op
de finishfoto.
5
6
De bovenste bal komt zesmaal op de foto bij de
finish: 6 × 0,001 = 0,006 s, dus 0,006 s is de
passeertijd van 6 cm bal.
Zijn snelheid is dus 0,06 m/0,006 s = 10 m/s.
De onderste bal komt 17 keer op de foto: 17 × 0,001 s =
0,017 s
De snelheid is dus 0,06/0,017 = 3,5 m/s.
Op de horizontale as staat een tijdschaal.
7 a 2000 Hz
De bovenste bal is op de foto 2 maal zo dun als
hoog. Door de frequentie 2 maal zo hoog te maken
komt de bal 2 keer zo vaak op de foto; dan wordt de
lengte ook 2 maal zo groot en komt de bal dus rond
op de foto.
b De onderste bal wordt dan ook 2 keer zo lang, dus
helemaal als een streep.
8
Heel kort, want hoe sneller hoe smaller.
9
De Duitsers komen met hun voorkant later over de
finish en met hun achterkant eerder. De boot van de
Nederlanders steekt met de steven voor de Duitse
boot uit en met de achterkant achter de Duitse boot
uit. De Nederlandse boot lijkt dus langer dan de
Duitse.
1.1 Snelheid meten
1 a Een eenheid van afstand (m, cm, km, …) en een
eenheid van tijd (s, min, h, …).
b m/s, mm/min, mijl per dag, mm/eeuw, cm/jaar
De eenheid van snelheid is een eenheid van afstand
gedeeld door een eenheid van tijd.
Let op: een lichtjaar is geen eenheid van tijd maar van
afstand!
2
3 a Lengte vrouw: ~ 1,7 m
Lengte haar: ~ 2 m
b 17 jaar
1 cm
200 cm
1 maand
200 maanden = 16 jaar en 8 maanden
Omdat je de lengte hebt geschat, rond je af op een
geheel aantal jaren.
c Na 18 maanden.
Maak een tabel met tijd en de haarlengte:
tijd
0 mnd
6 mnd
12 mnd
18 mnd
Linda
25 cm
31 cm →
21 cm
27 cm →
17 cm
23 cm →
13 cm
Chantal
0 cm
6 cm
12 cm
18 cm
Je ziet dat na 18 maanden Linda’s haar het kortst is
(nadat zij bij de kapper is geweest).
4 a 17 cm
b 43 cm/s = 0,43 m/s
17 cm
43,4 cm
0,3917 s
1s
c De tijd is veel te kort. Je reactietijd bij het indrukken
van de knoppen is zo groot dat de meting onnauwkeurig wordt.
d Het licht van het ‘lichtpoortje’ moet goed tegengehouden worden.
5 a s, min, h
b Omdat de tijd wordt gemeten. De afstand ligt vast.
c In de tweede kolom staat de snelheid in m/s en in
de vierde in km/h:
Usain Bolt
100 m
10,44 m
37578 m
37,6 km
9,58 s
1s
3600 s
1h
Florence Griffith-Joyner
100 m
9,53 m
34 318 m
34,3 km
10,49 s
1s
3600 s
1h
Patrick Makau Musyoki
42 200 m
5,69 m
20 480 m
20,5 km
7 418 s
1s
3600 s
1h
Paula Radcliffe
42 200 m
5,19 m
18 698 m
18,7 km
8 125 s
1s
3600 s
1h
Nee:
100 m
10,4 m
3600 × 10,4 m = 37,6 km
9,58 s
1s
1 uur
6
242759_NAT 3E TF HAVO 4 UW_CH01.indd 6
© Noordhoff Uitgevers bv
15/07/13 12:55 PM
Hoofdstuk 1 Bewegen in grafieken
c De afstand op de foto is 1,2 cm. In werkelijkheid dus
17 × 1,2 = 20 cm = 0,2 m. De tijd is 0,2 s.
De gemiddelde snelheid is dus 0,2/0,2 = 1 m/s.
Volgens de grafiek is de afstand ongeveer 22 cm, dat
geeft een snelheid van 1,1 m/s.
d Omdat hij bij de laatste flits nog niet helemaal
beneden is; en zijn val is ook al vóór de eerste flits
begonnen.
6 a 464 m/s = 1,7 · 103 km/h
Reken eerst de omtrek van de aarde uit op de breedtegraad van Singapore:
2πr = 2 × π × 6378 · 103 = 40,07 · 106 m
Deze afstand wordt in 24 h = 86400 s afgelegd.
86400 s
3600 s
1h
Dat is dus 464 m/s = 1,67 · 103 km/h
b Omdat Nederland op een grotere breedtegraad ligt
dan Singapore, is de afstand tot de aardas kleiner.
De omtrek is dus ook kleiner, maar de tijd blijft
gelijk. We bewegen dus met een kleinere snelheid
dan in Singapore.
11 a De afstand tot de sensor (de plaats) wordt dan
kleiner.
b
I
II
x
1s
7 a 28 m/s
De afstand bij een penalty is 11 m.
27,5 m
0,4 s
1s
b De tijd is veel te kort. De reactietijd bij het starten
en stoppen van de stopwatch is ongeveer 0,1 s.
c Maak een opname met een videocamera en speel
de opname beeld voor beeld af. Zorg ervoor dat de
stip en de doellijn zichtbaar zijn, zodat je kunt tellen
in hoeveel beeldjes de bal 11 meter aflegt. Je moet
ook weten hoeveel beelden per seconde de camera
maakt.
Of gebruik een laserstraal die onderbroken wordt,
met een lichtpoortje en een elektronische klok.
Het kan ook met een lasergun.
8
t
III
t
767 468 692 m
1s
2,56 s
t
12 a
De bal beweegt na de trap met vrijwel constante
snelheid. De bal legt dus steeds dezelfde afstand af
tussen twee opeenvolgende flitsen.
383 734 346 m
299 792 458 m
t
IV
x
11 m
x
1,67 · 106 m 1,67 · 103 km
x
40,07 · 106 m 463,8 m
b
Vergeet niet door 2 te delen.
De tijdsduur moet bovendien precies 2,56 s zijn
geweest, dus 2,56000000 s, anders is de uitkomst
ook niet zo nauwkeurig.
9 a 1e manier: met een stroboscoop.
2e manier: met een plaatssensor en een computer.
Het voordeel van een stroboscoop is dat de beweging met regelmatige intervallen op één foto wordt
vastgelegd.
Het voordeel van de computer is dat de beweging
meteen in een grafiek kan worden weergegeven.
b Een plaatssensor
10 a Van de eerste foto tot de onderste is (ongeveer)
11 cm op de foto en in de plaatsgrafiek 1,9 m. De
verkleining is dus 190/11, dus schaal 1 : 17.
b Hij gaat steeds sneller, want de afstand tussen twee
plaatjes neemt toe.
© Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_CH01.indd 7
Het steentje wordt, nadat het is losgelaten eerst
afgeremd door de zwaartekracht en gaat dus steeds
langzamer omhoog. Na het hoogste punt wordt het
steentje versneld door de zwaartekracht en valt steeds
sneller omlaag.
13
pulsje
7
15/07/13 5:55 PM
Hoofdstuk 1 Bewegen in grafieken
14
1.2 Plaatsgrafieken
d De betekenis van een snijpunt is dat de bewegende
voorwerpen op dat moment op dezelfde plaats zijn.
Ze komen elkaar op dat tijdstip en die plaats dus
tegen.
a3, b4, c1, d2, e5
15 a x
b De tijd kan niet negatief zijn.
16
17
Van 0 tot ongeveer 2,8 s vertraagd.
Van 2,8 tot ongeveer 7,7 s stilstand.
Van 7,7 tot bijna 11 s eerst versneld en dan weer
vertraagd tot stilstand.
Van 11 tot 14 s eerst versneld en dan vrijwel constante snelheid in omgekeerde richting.
20 a,b Voor alle duidelijkheid zijn ook de op de foto
gemeten waarden in de tabel gezet:
t in s x op de foto in cm x in werkelijkheid in m
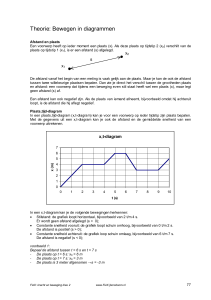
Hoe steiler de grafiek des te groter is de snelheid.
20 = 8,0 m/s
Δx = ___
18 a v = ___
Δt 2,5
24 = 8,0 m/s
Δx = ___
v = ___
Δt 3,0
80 = 8,0 m/s
Δx = ___
v = ___
Δt 10
b De plaatsgrafiek is een rechte lijn. (De grafiek is
overal even steil.) Dit betekent dat de snelheid
steeds hetzelfde is.
c Hellingsgetal (of: helling, steilheid, richtingscoëfficiënt,
rico)
d De plaatsgrafiek is een kromme. (De grafiek is niet
overal even steil.)
e Het hellingsgetal neemt toe, dus de snelheid ook.
f Hier zit een (vrijwel) recht stukje, dus (vrijwel)
constante snelheid.
g De grafiek loopt de eerste 4 seconden gemiddeld
het steilst. Dus is de gemiddelde snelheid dan groter
dan van de hele beweging.
In de eerste 4 seconden wordt 42 m afgelegd, dus:
42
vgem = ___
4,0 = 11 m/s
De hele beweging is 100 m in 12,2 s dus
100 = 8,20 m/s
vgem = ____
12,2
30
h vgem (van 3 tot 8 s) = ___
5 = 6 m/s
62 = 7 m/s
vgem (van 2 tot 11 s) = ___
9
19 a, b, c:
x in m
a
20
b
10
0
–10
–20
c
–30
–40
8
242759_NAT 3E TF HAVO 4 UW_CH01.indd 8
1
2
3
4
t in s
0
0,2
1,2
0,144
0,4
3,2
0,384
0,6
6,1
0,732
0,8
10,3
1,236
Omdat ‘het midden’ van de kat niet erg precies vast
ligt kunnen je uitkomsten enkele millimeter afwijken.
1,2
1
0,8
0,6
0,4
0,2
0
0
0,2
0,4
0,6
0,8
tijd in s
De vorm van de grafiek is hetzelfde als van
figuur 1.8, maar de afstanden zijn veel kleiner; in
opdracht 10 hebben we al gezien dat figuur 1.8 met
een andere schaalfactor is gemaakt.
De daar gevonden schaal is wel zo aannemelijk: bij
een schaal 1:12 is het katje maar ruim 20 cm lang.
21 a Met een zeer korte lichtflits
b Als de ballonnen 30 cm groot zijn dan is de foto
ongeveer 10 keer verkleind. De kogel staat als een
streepje van 2 mm op de foto; als hij rond is heeft hij
dus ongeveer 2 cm afgelegd.
c
850 m
0,02 m
1s
2,4 · 10–5 s
Dus minder dan 1/10 000 s: antwoord A.
Je kunt ook beredeneren dat hij met die snelheid
8,5 cm aflegt in 1/10 000 s, dat is veel meer dan op
de foto.
40
30
0
plaats in m
c
0
5
22 a Een voorwerp beweegt met constante snelheid
vooruit. Daarna keert hij om en beweegt iets
langzamer met constante snelheid terug. Na even
stil te hebben gestaan, gaat het voorwerp verder
terug met dezelfde snelheid, tot hij weer op de
beginpositie is teruggekeerd. Daar blijft het stil
staan.
© Noordhoff Uitgevers bv
15/07/13 12:55 PM
Hoofdstuk 1 Bewegen in grafieken
b Aflezen: 28 m.
c Tussen 0 en 20 seconden is de snelheid constant.
Dat is dus ook de snelheid op t = 12 s:
48
Δx = ___
= 2,4 m/s
v = ___
Δt 20
d Tussen 20 en 48 s is de snelheid ook constant.
Dat is dus ook de snelheid op t = 40 s:
(24 − 48) ____
Δx = ________
= −24 = −0,86 m/s
v = ___
∆t (48 − 20) 28
3
v in m/s
e
(negatieve snelheid, want het voorwerp beweegt
achteruit)
2,5
24
25 a Het is een stijgende of dalende rechte.
b Het is een kromme die steeds steiler wordt.
c De grafiek gaat over van stijgen in dalen of
omgekeerd.
d De grafiek kruist de tijd-as.
1.3 Snelheidsgrafieken
26 a v
b Dat betekent dat de snelheid steeds hetzelfde is:
constante snelheid.
c Dat betekent dat de plaats steeds hetzelfde is: het
voorwerp staat stil.
27
2
1,5
1
0,5
pulsje
A2, B3, C1, D5, E4
Grafiek D komt niet echt overeen met grafiek 5, want
in grafiek 5 keert het voorwerp vrijwel in één keer om
en in grafiek D duurt het afremmen en weer op gang
komen even.
28 a,c
0
–0,5
t in s
–1
0
0
0
–1,5
1
1
3,6
2
2
7,2
3
3
10,8
4
4
14,4
50
100
t in s
23 a 0 m/s
De grafiek begint horizontaal, dus de beweging
begint vanuit stilstand.
b De helling neemt toe.
400
c vgem = ____
45 = 8,9 m/s
___
Δx
Δt
300
= ____
40 = 7,5 m/s
e Teken een raaklijn bij t = 40 s of leg je liniaal er
nauwkeurig langs, dan vind je een helling van
ongeveer:
___
Δx
Δt
v in km/h
5
5
18
10
5
18
12
0
0
b,d de eerste 12 seconden horen bij vraag b, het
vervolg bij vraag d.
470
= _______
50 − 20 = 16 m/s
6
snelheid in m/s
d Bekijk de rode raaklijn; de helling is:
v in m/s
5
4
3
2
1
f
x
0
–1
–2
–3
–4
–5
–6
t
© Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_CH01.indd 9
2
4
6
8
10 12 14 16 18 20 22 24
tijd in s
1
c 1 m/s = ____
1000 × 3600 = 3,6 km/h
enzovoorts; zie de tabel hierboven.
9
15/07/13 12:55 PM
Hoofdstuk 1 Bewegen in grafieken
c
30 a
b
c
d
Als de snelheidsgrafiek steil omhoog loopt.
Als de snelheidsgrafiek horizontaal loopt.
Als de snelheidsgrafiek omlaag loopt.
aB; bA; cE
31
pulsje
32
a2; b1; c4; d3; e5
33 a, b, c
t
36 a Fout. De snelheid neemt in beide grafieken toe en
weer af. Als je terug gaat wordt de snelheid
negatief.
b Fout. Grafiek 2 stijgt iets sneller dan hij daalt. De
versnelling is dus groter dan de vertraging.
c Fout. Het horizontale stuk in de snelheidsgrafiek
betekent dat de snelheid een tijdje lang gelijk blijft.
Je staat dan niet stil.
a
b
30
40
v in km/h
v in m/s
40
Space Shot
lift
37 a
50
c
30
20
20
10
10
0
0
0
1
2
3
4
t in s
5
b
Teken de raaklijn bij de gegeven tijdstippen en
bepaal daarvan de helling.
26 − 3,0
Δv = _______
2
Voor t = 1,5 s: a = ___
3,0 = 7,7 m/s
Δt
32 − 21
Δv = ______
2
Voor t = 5,0 s: a = ___
7,0 = 1,6 m/s
Δt
2
4
6 8 10
t in h
50
40
30
20
10
0
Deze waarden zijn niet erg nauwkeurig te bepalen; je
kunt er makkelijk 0,5 m/s2 naast zitten.
35 a Van snelheid merk je niets als je niet naar buiten
kunt kijken, omdat je daarbij geen krachten ondervindt.
Je merkt het wel als hij versnelt en vertraagt, omdat
je dan wel een kracht ondervindt.
Je voelt bijvoorbeeld ook op geen enkele manier dat
de aarde draait, of dat de aarde met 30 km/s door het
zonnestelsel beweegt.
Een lift schommelt meestal wel een beetje, daardoor
voel je dat je beweegt.
b Niet alleen de snelheid, maar ook de versnelling
wordt geleidelijk groter en dan weer kleiner.
Daardoor neemt ook de kracht die je voelt geleidelijk toe en weer af.
0
De getallen hoeven er niet bij, maar het mag wel om
een idee te geven van de snelheden en tijden.
v in km/h
34
v
29 a Bepaal uit de grafiek of de tabel hoeveel m/s de
snelheid per s toeneemt: in 4 s is het 4 m/s, dus
a = 1 m/s2.
b a = –2,5 m/s2. Nu bepaal je de afname per seconde.
Het minteken geef aan dat het om een vertraging
gaat.
38
0
2
4
6 8 10
t in h
A: grafiek 3. De snelheid van Anja blijft (ongeveer)
gelijk, ze gaat nauwelijks omhoog of omlaag.
B: grafiek 1. Bas gaat de helling af dus zijn snelheid
neemt toe.
C: grafiek 2. Christa gaat eerst de helling af (snelheid
neemt toe) en dan weer omhoog (snelheid neemt af).
D: grafiek 4. Daan remt af want hij nadert een
afgrond.
30
Δv = ___
= 10 m/s2
39 a a = ___
Δt 3,0
b Ongeveer 31 m/s
c Bepaal de helling van het laatste rechte stuk
0 − 20 = −20 m/s2
Δv = ______
a = ___
7−6
Δt
v
Het minteken mag je ook weglaten omdat de
vertraging gevraagd wordt.
t
10
242759_NAT 3E TF HAVO 4 UW_CH01.indd 10
© Noordhoff Uitgevers bv
15/07/13 12:55 PM
Hoofdstuk 1 Bewegen in grafieken
Je kunt ook het oppervlak zo goed mogelijk verdelen
in een driehoek en een rechthoek en daarvan de
oppervlakte uitrekenen.
d Ongeveer 0,3 s. Nauwkeuriger is het niet af te lezen.
3
0
c Verplaatsing is 3 × 4 = 12 m
4
t in s
41 a 3,75 m.
De snelheid neemt toe van 0 tot 3 m/s, dus de
gemiddelde snelheid is 1,5 m/s. Vermenigvuldig dan
met Δt: 1,5 × 2,5 = 3,75 m.
Je kunt ook een driehoekje tekenen; de oppervlakte
daarvan is: _21 × 2,5 × 3 = 3,75 m.
b Ongeveer 15 meter.
In de eerste 5 seconden legt hij 15 m af. Het blauwe
oppervlak is ongeveer even groot.
42 a
b
c
d
2,5 s. Je hebt 2 hokjes in 5 seconden.
1 m/s
1 × 2,5 = 2,5 m
76 m
Tot t = 5 s: 6 hokjes;
van t = 5 s tot t = 12 s: 18 hokjes;
van t = 12 s tot t = 19 s: 6,5 hokjes.
Totaal dus 6 + 18 + 6,5 = 30,5 hokjes.
30,5 × 2,5 (= 76,25 m) = 76 m.
43 a 4 m/s
Trek de raaklijn in t = 0 s langs de grafiek en be-paal
het hellingsgetal. Je krijgt een fout antwoord
wanneer je de grafiek zelf gebruikt om v(0) te
be-palen, bijvoorbeeld door de verplaatsing tussen
t = 0 s en t = 0,1 s af te lezen (Δx = 0,34 m).
De grafiek is immers geen rechte lijn.
b De raaklijn aan de grafiek loopt dan horizontaal.
c Vlak vóór het hoogste punt en vlak ná het hoogste
punt is de snelheid klein. De basketballer gaat dus
even bijna niet omhoog of omlaag. Het lijkt dus
alsof hij een tijdje ‘stil’ hangt in de lucht. Bovendien
kan de sporter in de lucht zijn ledematen naar
beneden bewegen zodat zijn bovenlijf nog heel
even op dezelfde hoogte blijft.
44 a Gewoon aflezen: 0,5 m/s
In een snelheidsgrafiek is de snelheid constant als
de grafiek horizontaal loopt.
b 20 m/s
Teken een raaklijn bij t = 3 s en bepaal de helling:
33
Δx = ______
v = ___
= 19 m/s
Δt 3 − 1,3
c 1,1 m
Je moet het oppervlak onder de grafiek bepalen
tussen 0 en 2,5 s. Nauwkeurig tellen en delen van
hokjes schatten!
Het zijn 21 hokjes. Een hokje komt overeen met
0,1 · 0,5 = 0,05 m. Dus je vindt:
21 · 0,05 = 1,05 = 1,1 m.
© Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_CH01.indd 11
45
v
0
t
1.4 Bewegen in modellen
46 a, b, d Computermodel.
c Hoe sneller, hoe steiler.
47
De snelheidsgrafiek daalt, de plaatsgrafiek loopt
steeds minder steil.
48
Computermodel.
49 a Na 1 s is de snelheid verhoogd van 0 naar 0,5 en de
plaats is onveranderd gebleven.
b Na 2 en 3 s is de snelheid telkens met 0,5 verhoogd.
Na 2 s is de plaats met 0,5 verhoogd en na 1 s is de
plaats met 1 verhoogd.
50 a Na 1 s is de snelheid met 0,50 afgenomen en de
plaats met 10 toegenomen.
b Na 2 en 3 s neemt de snelheid steeds met 0,5 af. Na 2 s
is de plaats met 9,5 toegenomen en na 3 s met 9.
Opmerking: de antwoorden bij opdracht 49 en 50
gaan uit van gebruikte modellen met een stapgrootte van 1.
51 a De bal keert om: hij wordt teruggeslagen of kaatst
terug tegen een muur.
b
v
v in m/s
40 a, b
t
52 a 1 Het model van figuur 1.40 met snelheid 0 en een
beginpositie buiten de oorsprong.
2 Hetzelfde model als bij 1, maar nu met een
snelheid die niet nul is.
3 Het model voor de versnelde beweging van
figuur 1.42.
4 Het model van de vertraagde beweging van
figuur 1.44.
11
15/07/13 5:56 PM
Hoofdstuk 1 Bewegen in grafieken
t
3
t
2
t
4
t
v
v
1
55 a Onjuist
Fietser 2 fietst sneller dan fietser 1, zijn grafiek is
steiler. Fietser 2 vertrekt ook later dan fietser 1.
b Onjuist
De helling van de plaatsgrafiek is overal gelijk, dus
de snelheid blijft gelijk.
c Juist
De helling van de grafiek van fietser 3 is negatief, die
van 1 en 2 is positief.
d Onjuist
Ze fietsen in tegengestelde richting; ze komen
elkaar wel tegen.
e Juist
Fietser 3 bevindt zich eerst op dezelfde plaats als
fietser 2 (waar hun grafieken elkaar snijden) en
daarna ontmoet hij ook fietser 1.
56 a
53 a De grafieken die horen bij de versnelde beweging.
b Een val van 10 m duurt 1,4 s; de snelheid is dan
14 m/s.
c Computermodel
d k = 0,01
e Dan is k kleiner. Hoe kleiner k des te kleiner is de
vertraging, dus des te minder heb je last van
luchtweerstand.
f Lichtere voorwerpen worden meer vertraagd door
de luchtweerstand en zullen dus een grotere k
hebben.
54 a 2 uur
1 uur heen en 1 uur terug
b Nee; je fietst veel langer 10 km/h dan 30 km/h, dan
is het gemiddelde niet 20 km/h.
c Heen fiets je 40 minuten (= _23 uur) 30 km/h, terug
fiets je 2 uur lang 10 km/h.
d 15 km/h
De totale tijd is 2_23 uur = 2,667 h
40
___ = _____
vgem = Δx
= 15 km/h
Δt 2,667
e
Jan
Kim
10
0
0
5
10
15
20
25 30 35
t in min
de s moet x zijn.
b 10 minuten na het vertrek van Chantal.
c 1,3 min. Dat is alleen af te lezen als je de grafiek flink
groot tekent. Je kunt het ook uitrekenen:
267 s nadat hij vertrokken is, zwaait Jan naar Kim; 343
s na zijn vertrek zwaait hij naar Chantal. Het verschil
is 76 s = 1,3 min.
57 a Dan wordt de vertraging in één keer veel groter; op
dat moment gaat de parachute open.
b Als je k kleiner maakt wordt de luchtweerstand
kleiner en dus de snelheid groter. Bij een waarde van
0,001 is de eindsnelheid vrijwel 100 m/s.
c
20
4000
15
10
5
0
Chantal
5
afstand in m
x in km
25
Naar school
15
x in km
v
v
b
0
0,5
1
1,5
zonder wind
2 2,5
t in h
3
met wind
f A is het juiste antwoord.
Bij tegenwind verlies je altijd meer tijd dan je wint
met de wind mee.
g Computermodel, als het goed is krijg je dezelfde
grafieken als in vraag e.
12
242759_NAT 3E TF HAVO 4 UW_CH01.indd 12
3600
3200
2800
2400
2000
1600
1200
800
400
0
0
50
100
150
200
250
300
t in s
© Noordhoff Uitgevers bv
15/07/13 12:55 PM
Hoofdstuk 1 Bewegen in grafieken
d
e
f
g
De getallen hoeven er niet bij, maar het mag wel om
een idee te geven van de afstand en de tijd.
225 km/h = 62,5 m/s
Bij 3000 m wordt de vertraging dus 0,4 × 62,52 –
9,81 = 1553 m/s2. Bij zo’n vertraging word je uit
elkaar gerukt.
Bij een te kleine tijdstap, bijvoorbeeld 1 s, wordt de
snelheid in een stap negatief (volgens het model
vliegt de parachutist dan weer terug de lucht in!!)
Computermodel
Het open gaan van de parachute duurt even, dat is
in het model niet goed beschreven. De landingsmanoeuvre zit ook niet in het model.
10
Dat komt omdat de snelheid negatief is.
Als je dan gaat afremmen, d.w.z. dat de snelheid
richting nul gaat, dan stijgt de grafiek.
11
Tijdens het afremmen is de gemiddelde snelheid
weer 5 m/s, dus legt hij 5 × 1,8 = 9 m af.
Dat is meer dan de 6,0 m die er na de finish is, dus
deze deelnemer valt in het water.
12
Als je gelijkmatig afremt van 10 m/s tot nul dan is de
gemiddelde snelheid altijd 5 m/s, ongeacht de
vertraging. Hij mag dus niet meer afleggen dan 6
meter met een gemiddelde snelheid van 5 m/s; dat
duurt 1,2 s.
Toepassing
Opgave 1 Space Shot
1
Door op verschillende tijdstippen de raaklijn aan de
grafiek te tekenen, vind je de versnelling op deze
tijdstippen. Met deze gegevens kun je de versnellingsgrafiek tekenen.
De maximale snelheid is 21 m/s. Dat is 76 km/h, dus
geen 85 km/h.
3
Na 3,6 s wordt de snelheid negatief. Daar keert hij
om en dat is dus het hoogste punt.
4
In het begin is de grafiek het steilste. Teken daar een
raaklijn; die heeft een helling van ongeveer 30 m/s2.
De 40 m/s2 wordt dus niet gehaald.
5
10 = 8,3 m/s2
Δv = ___
a = ___
Δt 1,2
Let op dat je de snelheidsverandering (Δv) niet
verwart met de gemiddelde snelheid (vgem).
13
10
Je kunt een zo goed mogelijk passende driehoek
tekenen en dan de oppervlakte bepalen:
v in m/s
5
0
–5
25
–10
20
5
10
15
20
tijd in s
Met de punten (0 s; 10 m/s) en (20 s; −5,4 m/s)
vinden we voor het hellingsgetal:
15
10
v2 − v1 −5,4
− 10
Δv = _____
2
= ________
a = ___
20 − 0 = −0,77 m/s
Δt t2 − t1
5
0
De versnelling haal je uit de snelheidsgrafiek m.b.v.
een raaklijn:
snelheid in m/s
2
Dan is de vertraging:
0
1
2
3
4
0,5 × 3,6 × 24 = 43 m
Opgave 2 Heen en weer
6
Op de schans versnellen de deelnemers in 2 seconden vanuit stilstand tot 10 m/s; de gemiddelde
snelheid is dus 5 m/s.
Dus de lengte van de schans is 5 × 2 = 10 m
7
Tussen de eerste en de tweede schans rijden ze 3,2 s
met een snelheid van 10 m/s, dus de afstand is 32 m.
8
Als de snelheid weer nul is, dus na 7,5 s.
9
Ze remmen van t = 13,2 s tot t = 15 s, dus in 1,8 s
neemt de snelheid af van 10 m/s tot nul.
10 = 5,6 m/s2
Δv = ___
a = ___
Δt 1,8
© Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_CH01.indd 13
14
Het hoogste punt op de 2e schans is het punt dat de
snelheid weer nul is geworden. Dat is op het tijdstip
t = 8,4 s. De afgelegde afstand vinden we door
hokjes te tellen.
Eén hokje stelt een afstand van 1 m voor.
Van 0 s tot 8,4 s tellen we onder de grafiek 44
hokjes, dus de afstand = 44 m.
15
Het parcours blijft natuurlijk even groot, maar
omdat er sprake is van weerstand komt het voertuig
minder hoog op de 2e schans. In totaal legt het
voertuig dan ook minder af naar de finish.
Opgave 3 Parachute
16 In de bovenste grafiek is de snelheid voordat de
parachute opengaat het grootste.
Die snelheid is (4500–1000)/(56 – 10) = 76 m/s.
13
15/07/13 12:55 PM
Hoofdstuk 1 Bewegen in grafieken
17
Het laatste deel van beide grafieken loopt even steil,
dus met dezelfde snelheid.
18
Aan de helling van de grafiek kun je zien dat de
snelheid bij het open gaan van de parachute bij de
sprong van 800 m kleiner is dan bij de sprong van
5 km. Als de snelheid kleiner is, dan is er ook minder
luchtweerstand op de parachute, dus een kleinere
vertraging.
v
19
5000 m
800 m
27
De duur van een puls is gelijk aan de tijd die het
geluid nodig heeft om 40 cm heen en terug af te
leggen, dat is dus 0,8 m. De geluidssnelheid bij 20 °C
is 343 m/s (Binas tabel 15 bij 293 K).
De tijd is dan 0,8/343 = 0,0023 s (= 2,3 ms).
Opgave 6 Auto
28 Op de foto is de breedte van het achterwiel ongeveer 2,5 maal zo groot als de hoogte. Dus heeft de
auto zich tijdens het maken van de foto 1,5 wieldiameters verplaatst.
Een auto is ongeveer anderhalve meter hoog, Voor de
diameter van een wiel schatten we een halve meter.
Voor de snelheid geldt dan:
1,5 × 0,5
v = _s = _______ = 23 m/s
1/30
t
Proefwerkopgaven
t
Opgave 4 Zwemmers
20 Alle mensen hebben vrijwel dezelfde dichtheid, dus
als ze even zwaar zijn dan hebben ze ook hetzelfde
volume.
Het volume is evenredig met de dwarsdoorsnede A
en de lengte l. Naarmate A groter is, moet l dus
kleiner zijn.
22
23
1350
vgem = ____
50 = 27 m⁄s (= 97 km/h)
c
Blok 1 heeft een eindsnelheid van 0,90 m/s en blok 2
heeft een snelheid van 0,96 m/s.
De eindsnelheid van blok 2 is dus 0,06 m/s groter.
Dat is 0,06/0,90 × 100% = 6,7%. Dus dat klopt
ongeveer.
Blok 1 gaat gedurende ongeveer 0,9 s 0,06 m/s
sneller. En legt in die tijd dus 0,054 m extra af. Maar
blok 2 gaat 0,06 s langer door met een snelheid van
0,9 m/s. Dat is dus een afstand van 0,054 m extra.
Beide blokken leggen dus een even grote afstand af.
Je kunt ook de oppervlakte onder beide grafieken
bepalen, maar dat is veel meer werk.
t in s
x in m
0
0
10
110
20
310
30
640
40
1080
50
1350
d,e
1600
x in m
21
1 a 50 s
Tussen elke twee foto’s zit 0,10 s.
b Hij heeft in die tijd 1,35 km afgelegd, dus
25
In 0,7 s is de afstand afgenomen van 1,36 m naar 0,4 m.
Dus is de snelheid 0,96/0,7 = 1,37 m/s.
Let op bij het aflezen van de plaats: 0,1 m komt
overeen met 4 mm!
26
Hij loopt met een snelheid van 1,37 m/s gedurende
2,5 s. De afstand is dus 1,37 × 2,5 = 3,4 m.
14
242759_NAT 3E TF HAVO 4 UW_CH01.indd 14
1200
1000
800
600
400
De helling van beide grafieken is in het begin
hetzelfde. Dus dezelfde versnelling ondanks
verschillende doorsnede.
Opgave 5 De bewegingssensor
24 Bij een hogere temperatuur is de geluidssnelheid
groter. De puls is dan eerder terug, waardoor de
sensor een te kleine afstand meet.
1400
200
0
0
10 20 30 40 50 60
t in s
e Raaklijnmethode (zie de grafiek):
900
Δx = ____
v = ___
45 = 20 m⁄s (= 72 km⁄h)
Δt
f Nee
De snelheid op de tweede foto (t = 10 s) is 66 km/h,
op de derde foto (t = 20 s) is dat 120 km/h. Voor de
snelheid bij t = 15 s zou je ongeveer het gemiddelde
van deze twee snelheden verwachten, dus
v1 + v2
______
2
66 + 120 = 93 km/h
= ________
2
© Noordhoff Uitgevers bv
15/07/13 12:55 PM
Hoofdstuk 1 Bewegen in grafieken
2 a Je moet alle snelheden delen door 3,6 om er m/s van
te maken, dan krijg je:
t in s
v in m∕s
0
0
10
18,3
20
33,3
30
43,9
40
43,6
50
14,2
40
snelheid in m/s
b
50
v in m/s
3 a Bij het blok snelheid kun je dubbelklikken en dan de
waarde invullen.
b De eindsnelheid is 16 m/s.
Dan is dus de versnelling gelijk aan de vertraging:
9,8 = k · 162
k = 9,8/162 = 0,038
c Teken de raaklijn bij t = 0 en bepaal de helling:
36
32
28
40
24
30
20
20
16
10
12
0
0
c Aan het begin (t = 0 s) en op het eind (tussen 40
en 50 s).
De versnelling is het grootst wanneer de grafiek het
steilst is.
Aan het begin is de snelheidstoename per seconde het
grootst (grootste versnelling), op het eind is de
snelheidsafname per seconde het grootst (grootste
vertraging).
18 – 0 = 1,8 m/s2
Δv = ______
d Aan het begin: a = ___
Δt 10 – 0
14 – 44
Δv = _______
= –3,0 m/s2
Op het eind: a = ___
Δt 50 – 40
Eigenlijk moet je dan raaklijnen tekenen, maar het
eerste en laatste stuk van de grafiek zijn bijna recht
(voor zover je dat kunt beoordelen met zo weinig
meetpunten).
© Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_CH01.indd 15
8
10 20 30 40 50 60
t in s
4
0
a=
0
0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0
t in s
–30
___
Δv ____
2
Δt
= 1,35 = –22 m/s
d De afstand is de oppervlakte onder de grafiek.
Eén hokje is 0,5 × 5 = 2,5 m. Er zijn ongeveer 34
hokjes, dus 34 × 2,5 = 85 m.
In de grafiek in het boek is de verticale as anders
geschaald. Dan kom je op 34 hokjes. In de grafiek hierboven tel je ongeveer 44 hokjes. Dat komt overeen
met 44 × 2 = 88 m. Bij een bepaling wordt daarom
altijd een marge toegestaan in het antwoord.
15
15/07/13 12:55 PM
Hoofdstuk 2 Bewegen en rekenen
Hoofdstuk 2
Bewegen en rekenen
1
Introductie
Bij de eerste testrit vloog de slee veel te ver door. Als
de rails lang genoeg zijn dan is dat geen probleem,
maar als de slee van de rail af vliegt moet je maar
afwachten waar hij terecht komt en hoe.
Bij de tweede test zou de proefpersoon te pletter
zijn geslagen tegen het houten scherm.
2
Sommige mensen vonden het een onnodige
vrijheidsbeperking of hun eigen verantwoordelijkheid. Anderen waren bang dat ze niet op tijd uit de
auto konden komen als die te water zou raken of in
brand vliegen.
3
Zijn wangen, lippen en haren komen naar voren
tijdens het afremmen. Alles wat ‘los’ zit schiet
tijdens het remmen nog even door. Hij zit dus met
het gezicht naar voren.
Als hij afremt met zijn rug naar voren dan vallen zijn
wangen en lippen juist in en gaan zijn haren naar
achteren.
4
Omdat dat comfortabeler is voor de reizigers en ze
dan minder snel luchtziek worden. Bovendien is de
kans op een ongeluk heel erg klein, en als een
vliegtuig écht crasht dan maakt het weinig uit hoe
je zit.
5
Als zijn ogen met bloed doorlopen waren dan kwam
tijdens het remmen het bloed in zijn hoofd kennelijk
naar voren, dus zat hij met zijn gezicht naar voren.
6
De Sonic Wind remde af door watertanks kapot te
rijden.
7
4 g is al heel wat; in de praktijk gaan attracties tot
ongeveer 5 g; de ‘Tower of Terror’ in Johannesburg is
wereldkampioen met 6,3 g. Voor korte tijd (minder
dan een seconde) is dat aanvaardbaar.
8
De ‘Wet van Murphy’: Alles wat mis kan gaan, gaat
een keer mis.
2.1 Snelheid
1 a Als de snelheid constant is, oftewel bij een eenparige rechtlijnige beweging.
b Bij een optrekkende auto, een remmende fiets, een
startende raket, een vallende steen, een schommel, …
c 10 km
Als je 20 km per uur fietst dan doe je in een half uur
de helft van 20 km. 20 × 0,5 = 10 km
16
242759_NAT 3E TF HAVO 4 UW_CH02.indd 16
2 a Zie Binas tabel ‘Planetenstelsel’.
De gemiddelde afstand van de Aarde tot de Zon is
0,1496 · 1012 m, die van Mars tot de Zon is
0,2278 · 1012. De afstand tussen beide planeten is het
kleinst als de drie hemellichamen als volgt op één
lijn staan: Zon – Aarde – Mars.
De kleinste afstand is dus
0,2278 · 1012 – 0,1496 · 1012 = 7,82 · 1010 m.
Voor het rekenen met machten van tien, zie bron 19.
b 1) Gegeven: s = 7,82 · 1010 m en t = 1 jaar.
Gevraagd: v = ? m/s
2) s = vt
3) Omdat v in m/s moet, moet t in seconden!
t = 1 jaar = 1 × 365 × 24 × 60 × 60 = 3,15 · 107 s
s = vt ⇒ 7,82 · 1010 = v × 3,15 · 107
7,82 · 1010
v = ________
= 2483 m/s = 2,48 · 103 m/s.
3,15 · 107
Wie secuur wil werken vult voor een jaar 365,25 dagen
in, omdat er elke vier jaar een extra dag is. Dan komt
er 2478 m/s uit. Als je de uitkomst een beetje afrondt
maakt het in dit geval geen verschil.
3
Antwoord: E,B,C,A,D
Om ze te kunnen vergelijken moet je eerst alle
eenheden gelijk maken b.v. alles in m/s
A 5,00 m/s
5000 m
= 1,39 m/s
B 5 km/h = _____ ___
3600 s
125 000 _
C _________ _m
= 1,45 m/s
24 × 3600 s
500 m
D ______ = 8,33 m/s
60 s
50 000 m
________________
E
= 0,00159 m/s
365 × 24 × 3600 s
4 a 1) Gegeven: v = 25 cm/min
Gevraagd: v = ? m/s
2) v = 25 cm in 1 minuut = 0,25 m in 60 seconden
0,25
dat is ____ m in 1 seconde = 0,00417 m/s
60
In 1 h kan hij 3600 × zoveel afleggen:
0,00417 × 3600 m = 15 m = 0,015 km
dus v = 0,015 km/h.
b 1) Gegeven: v = 21 km/h
Gevraagd: v = ? m/s
2) v = 21 km in 1 uur = 21000 m in 3600 seconden
21000 m in 1 seconde = 5,83 m/s
dat is ______
3600
c Gegeven: v = 5,0 m/s, t = 45 minuten
Gevraagd: s = ? m
Omdat de snelheid in m/s is, moet de tijd in
seconden: 45 minuten = 60 × 45 = 2700 seconden.
s = vt = 5,0 × 2700 = 13500 m = 13,5 km.
© Noordhoff Uitgevers bv
15/07/13 12:31 PM
Hoofdstuk 2 Bewegen en rekenen
d Gegeven: v = 5 cm/kwartier en t = 2 h
Gevraagd: s = ? m
Hier kun je het makkelijkst rekenen met
verhoudingen: 2 uur is 8 kwartier, dus dan legt hij
8 × 5 cm = 40 cm af, dat is 0,40 m.
In tabelvorm:
afstand in cm
5
40
tijd in kwartier
1
8
b Gegeven:
1) 30 min met 100 km/h,
2) 20 min met 120 km/h,
3) 5 min met 0 km/h.
Gevraagd: s = ? km.
Oplossing:
1) 100 km/h dus in 30 min (= _21 h)
_1
s = vt = 100 × 2 = 50 km,
2) 120 km/h dus in 20 min.(= _31 uur)
s = vt = 120 × _31 = 40 km.
3) 0 km
Als je stilstaat, dan leg je geen afstand af.
totaal: s = 50 + 40 = 90 km
c De totale tijd is:
55
30 + 20 + 5 min = 55 min = ____ = 0,917 h.
60
90
afstand = ______
vgem = ________
0,917 = 98 km/h.
tijd
Natuurlijk kun je ook de snelheid omrekenen in m/s
en de tijd in seconden, maar dat is veel meer werk.
e Gegeven: v = 2,5 km/h, en s = 500 m
Gevraagd: t (in minuten)
Ook dit gaat snel met verhoudingen:
500 m is _51 deel van 2,5 km; daar doet hij dus
60
_1
___
5 uur over, dat is 5 = 12 minuten.
Of in tabelvorm:
afstand in m
2500
500
tijd in min
60
12
5 a Gegeven:
afstand Kreta-Nederland = 2400 km;
dat moet in meter en omdat het bericht heen en
terug gaat moet je de afstand dubbel nemen:
s = 4 800 000 m,
v = 3,0 · 108 m/s.
Gevraagd t = ? s.
s = vt
4 800 000 = 3,0 · 108 × t
4 800 000
= 0,016 s.
dus t = __________
3,0 · 108
b De snelheid van de bus is:
4000
v = _____ = 6,66… = 6,7 m/s (= 24 km/h).
600
Gegeven:
t = 0,016 s (zie a),
v = 6,66… m/s
Gevraagd: s = ? cm.
s = vt = 6,66 × 0,016 = 0,11 m = 11 cm.
in tabelvorm:
6
afstand (m)
4000
0,11
tijd (s)
600
0,016
Δx
1) Totale afstand delen door de tijd: vgem = ___
Δt
2) Gemiddelde nemen van begin- en eindsnelheid:
1
vgem = __
2 (vbegin + veind)
Methode 2 mag je alleen gebruiken als de snelheid
gelijkmatig verandert.
7 a Eerst de gemiddelde snelheid uitrekenen:
vgem = _21 (100 + 120) = 110 km/h.
110000 m = 30,6 m/s
dat omrekenen naar m/s: _________
3600 s
dan s = vgem t = 30,6 × 5,0 = 153 m = 0,15 km
© Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_CH02.indd 17
d Het optrekken en afremmen duurt alles bij elkaar
maar enkele tientallen seconden, op de totale tijd
van 55 minuten is dat te verwaarlozen.
8
Gegeven:
vbegin = 0 km/h,
veind = 250 km/h en
t = 30 s.
Gevraagd: s = ?
125 000 m
250 + 0
= 125 km/h = __________
vgem = _______
2
3600 s
= 34,7 m/s.
s = vgem t = 34,7 × 30 = 1041 m = 1,04 km.
9 a Het gemiddelde van 80 en 110 is 95, maar hij rijdt
veel langer 80 km/h dan 110 km/h, dus de gemiddelde snelheid zal zeker minder zijn dan 95 km/h.
80 000 m = 22,2 m/s
b 80 km/h = _________
3600 s
c s = vt = 22,2 × 80 = 1778 m = 1,78 km
110 000 m = 30,6 m/s
d 110 km/h = __________
3600 s
s = vt = 30,6 × 20 = 611 m
e Eerst de gemiddelde snelheid tijdens het versnellen
berekenen:
95000 m
vgem = _21 (80 + 110) = 95 km/h = _________ = 26,4 m/s
3600 s
Hij versnelt gedurende 20 seconden, dus:
s = vgem t = 26,4 × 20 = 528 m = 0,53 km.
f De totale verplaatsing is 1778 + 611 + 528 = 2917 m
2917 m
de gemiddelde snelheid is _______
120 s = 24,3 m/s
(dat is 87,5 km/h)
10 a 220 km/h
Omdat je in tegengestelde richting rijdt, tel je de
snelheden op.
b 8,18 s
220 km/h = 61,11 m/s,
dus s = v · t wordt 500 = 61,11 × t
500
dus t = ____ = 8,18 s.
61,11
17
15/07/13 12:31 PM
Hoofdstuk 2 Bewegen en rekenen
11 a 1,59 s
De tijd van Sven:
gedurende de eerste 0,5 s neemt de snelheid toe
van 0 tot 2 m/s, dus het gemiddelde is 1 m/s:
s = vgem t = 1 × 0,5 = 0,5 m.
Tweede manier:
Bepaal de oppervlakte onder de grafiek van t = 0 s
tot t = 0,5 s:
A = _21 × basis × hoogte = _21 × 0,5 × 2 = 0,5 m.
c 1,5 m
Eerste manier:
tussen 0,5 s en 1,0 s neemt de snelheid toe van 2 tot
4 m/s, dus het gemiddelde is 3 m/s
s = vgem t = 3 × 0,5 = 1,5 m.
400
t = ____ = 31,75 s
12,6
de tijd van Olof:
400
t = ____
12,0 = 33,33 s
dus het tijdverschil is 33,33 – 31,75 = 1,59 s
b 11,1 minuten
Op dat moment heeft Sven 400 m meer afgelegd,
met een relatieve snelheid van 0,6 m/s duurt dat:
Tweede manier:
Bepaal de oppervlakte onder de grafiek van
t = 0,5 tot t = 1,0 s; die kun je verdelen in een
rechthoek (I) en een driehoek (II):
667
400
t = ____ = 667 s = ____ = 11 minuten
0,6
60
c 4 rondjes
In die tijd heeft hij 12,6 × 667 = 8400 m afgelegd,
v in m/s
8400
dat is _____
400 = 21 rondjes.
10 km is 25 rondjes, dus hij moet nog 4 rondjes.
II
12 a 10 s
De relatieve snelheid is 108 – 90 = 18 km/h =
5,0 m/s, om 50 m meer af te leggen dan de vrachtauto heb je dus 10 s nodig.
b 90 km/h
Die auto is 550 m dichterbij gekomen in 10 s, dus de
relatieve snelheid is 55 m/s = 198 km/h.
Als jij 108 km/h rijdt dan rijdt hij 198 – 108 =
90 km/h.
13 a De straal van de aarde is 6,378 · 103 km
zie Binas bij “Planetenstelsel”
b 26378 km
De straal van de cirkel die hij draait is de straal van
de aarde + de hoogte:
r = 6378 + 20000 = 26378 km
c 165738 km
De omtrek is 2πr = 2 × π × 26378 km = 165738 km
d 3,85 · 103 m/s
De omlooptijd is (11 × 60) + 58 min = 718 min
= 43080 s
De snelheid is dus:
165738 km
v = __________ = 3,85 km/s
43080 s
e 0,0667 s
Het signaal gaat met de lichtsnelheid, die is
300 000 km/s, de afstand is 20 000 km,
20 000
daarover doet het signaal dus ________
300 000 = 0,0667 s
f 257 m
s = v · t = 3,85 × 0,0666… = 0,256 km = 257 m
2.2 Versnellen
14 a De grafiek begint horizontaal.
dus niet: “hij begint bij nul”; dat zegt wel iets over de
plaats maar niets over de snelheid!
b 0,5 m
Eerste manier:
18
242759_NAT 3E TF HAVO 4 UW_CH02.indd 18
I
t in s
oppervlakte I = 0,5 × 2 = 1 m
oppervlakte II = _21 × 0,5 × (4 – 2) = 0,5 m
dat is samen 1,5 m
12 = 3,0 m/s2.
Δv = ___
15 a a = ___
Δt 4,0
b 24 m
De snelheid neemt toe van 0 tot 12 m/s, dus de
gemiddelde snelheid is 6 m/s:
dan s = vgem t = 6 × 4 = 24 m
16
180 m/s
Als je de versnelling en de tijd weet kun je op
verschillende manieren de snelheid uitrekenen.
Reken eerst de gegevens om:
100 km/s2 = 100 000 m/s2
1,8
1,8 ms = _____
1000 = 0,0018 s
De snelheidstoename is 100 000 m/s per seconde;
dus na 0,0018 s is de snelheid 100 000 × 0,0018 =
180 m/s.
in tabelvorm:
snelheidstoename in m/s
100 000
180
tijd in s
1
0,0018
Of met de formule:
Δv dus Δv = 100 000 × 0,0018 =
100 000 = _______
0,0018
180 m/s,
omdat de beginsnelheid nul was is de snelheid dan
ook 180 m/s.
© Noordhoff Uitgevers bv
15/07/13 12:31 PM
Hoofdstuk 2 Bewegen en rekenen
In 3,7 s legt hij dan af:
s = vgem t = 6,48 × 3,7 = 24 m en dat klopt met de
gegevens
Je kunt dit ook in een andere volgorde uitrekenen,
maar je moet ergens de gegeven 3,7 s gebruiken en
dan laten zien dat de gegeven getallen kloppen.
b De hond moet dan 36 m afleggen in 3,7 s:
De helling neemt geleidelijk af.
v
17
36 m
vgem = _____
3,7 s = 9,73 m/s
t
18 a 295 m
Toen de auto begon met afremmen was de afstand
400 m; tijdens het remmen heeft hij 400 m
afgelegd (en is dus op de plek waar eerst de laatste
auto van de file was).
De laatste auto van de file heeft in dezelfde tijd
afgelegd: s = vt = 19,4 × 15,2 = 295 m
(70 km/h = 19,4 m/s)
Dus de afstand is nog 295 m.
b 131 m
vbegin = 70 km/h = 19,4 m/s
veind = 100 km/h = 27,8 m/s
__
1
1
vgem = __
2 (vbegin + veind) = 2 (19,4 + 27,8) = 23,6 m/s
∆v = 27,8 – 19,4 = 8,33 m/s
(het bovenstaande kan iets sneller door eerst vgem en
∆v in km/h uit te rekenen en dan pas om te rekenen
naar m/s)
Δv of met een verhoudingstabel kun je nu
met a = ___
Δt
uitrekenen dat Δt = 5,56 s,
dan is s = vgem t = 23,6 × 5,56 = 131 m
19 a 13,9 m/s
vbegin = 0 km/h = 0 m/s
veind = 100 km/h = 27,8 m/s
De gemiddelde snelheid is 50 km/h = 13,9 m/s.
b s = vgem t = 13,9 × 4,3 = 59,7 = 60 m
c 107 m
vbegin = 120 km/h = 33,3 m/s
veind = 0 km/h = 0 m/s
De gemiddelde snelheid tijdens het remmen is
60 km/h = 16,67 m/s, de snelheidsverandering Δv is
120 km/h = 33,3 m/s.
Δv →
De remtijd kun je uitrekenen met a = ___
Δt
33,33
33,33
5,2 = _____ → Δt = _____
5,2 = 6,41 s
Δt
De remafstand is dus vgem t = 16,67 × 6,41 = 107 m
d 5,2 m/s
De vertraging is 5,2 m/s2, elke seconde neemt de
snelheid 5,2 m/s af, dus één seconde voordat hij stil
staat is de snelheid nog 5,2 m/s.
19,5
Δv = ____
a = ___
= 5,3 m/s2
Δt 3,7
dus dat zal hem niet lukken.
Je kunt ook uitrekenen dat hij met een versnelling van
4,5 m/s2 in 3,7 s een snelheid bereikt van 16,7 m/s, en
een afstand aflegt van 30,8 m, dus te weinig.
21
Gegeven: vbegin, veind en s
Gevraagd: a
Voor de vertraging moet je de snelheidsverandering
en de remtijd weten. Omdat de eindsnelheid nul is
weet je de snelheidsverandering.
De remtijd kun je uitrekenen met behulp van de
verplaatsing (die gegeven is) en de gemiddelde
snelheid.
De gemiddelde snelheid kun je uitrekenen omdat je
de begin- en de eindsnelheid weet.
Je gaat dus achtereenvolgens:
- de gemiddelde snelheid uitrekenen met:
1
vgem = __
2 (vbegin + veind)
- dan de remtijd uitrekenen met s = vgem t
Δv
- dan de vertraging uitrekenen met a = ___
Δt
22 a In de technische betekenis van de versnelling van de
auto, d.w.z. een van de verschillende tandwieloverbrengingen tussen de motor en de wielen.
In de natuurkundige betekenis van de snelheidsverandering per seconde
b 2,86 m/s2
Δv = 100 km/h = 27,78 m/s, dus:
27,78
Δv = _____
2
agem = ___
9,7 = 2,86 m/s
Δt
c Dan neemt de snelheid af.
d Tijdens het schakelen is er geen aandrijfkracht, maar
wel weerstandskracht waardoor de auto wordt
afgeremd.
e De helling van de snelheidsgrafiek is de versnelling;
deze wordt dus kleiner na elke keer schakelen, en is
negatief tijdens het schakelen:
v
20 a De eindsnelheid van de kat kun je uitrekenen met
Δv :
een verhoudingstabel of met de formule a = ___
Δt
___
Δv
3,5 = 3.7 dus Δv = 3,5 × 3,7 = 12,95 m/s,
c Als de beginsnelheid nul is en de gemiddelde
snelheid 9,73 m/s, dan moet de eindsnelheid
2 × 9,73 = 19,5 m/s zijn.
De versnelling moet dan zijn:
omdat de beginsnelheid nul was is de snelheid dan
ook 12,95 m/s.
1
De gemiddelde snelheid is dan __
2 (0 + 12,95) =
6,48 m/s.
t
© Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_CH02.indd 19
19
15/07/13 5:57 PM
Hoofdstuk 2 Bewegen en rekenen
40
Δx = ___
23 a vgem = ___
10 = 4,0 m/s
Δt
b Δv = 27 km/h = 7,5 m/s, dus:
d
v
7,5
Δv = ___
agem = ___
= 0,75 m,/s2
Δt 10
De snelheid is het kleinst op aarde met lucht.
Met luchtweerstand neemt op aarde de versnelling snel
af tot nul, dus wordt de snelheid snel constant en blijft
klein. Op de maan blijft de snelheid wel toenemen.
C
c De beginsnelheid is nul, de eindsnelheid 7,5 m/s;
als de versnelling constant was geweest dan zou de
gemiddelde snelheid 3,75 m/s geweest zijn.
A
24 a ∆v = 100 km/h = 27,78 m/s
B
27,78
Δv = _____
2
agem = ___
11,5 = 2,42 m/s
Δt
b vgem = 50 km/h = 13,89 m/s, dus
s = vgem t = 13,89 × 11,5 = 160 m
c 41,7 s
De totale testrit is 1000 m, dus hij rijdt
1000 – 160 = 840 m met een constante snelheid
van 27,78 m/s,
met s = vt reken je uit dat dat 30,2 s duurt.
Dus de totale tijd is 11,5 + 30,2 = 41,7 s.
d De versnelling tijdens het optrekken is niet constant,
dus de gemiddelde snelheid en de afgelegde afstand
tijdens het optrekken zijn niet juist (vraag b).
De werkelijke tijd is korter, dus tijdens het optrekken
legt hij meer af dan 160 m, dat betekent dat de
gemiddelde snelheid groter is dan 50 km/h.
25 a De beginsnelheid is nul, dus Δv = 4,5 m/s,
18 ms = 0,018 s, dus
4,5
Δv = _____
agem = ___
= 250 m/s2
Δt 0,018
b De versnelling van de vlo is 20 keer zo groot als van de
sprinkhaan, dus de tijd die hij nodig heeft om die
snelheid te krijgen is 20 keer zo klein: 0,9 ms = 0,0009
s.
Dus s = vgem t = 2,25 × 0,0009 = 0,002 m = 2 mm
c Conclusie 1: Als de versnelling 20 keer zo groot is, is
de afstand om dezelfde snelheid te bereiken 20 keer
zo klein.
Δv
Omdat a = __
is a omgekeerd evenredig met Δt. Dus a
Δt
20 keer groter geeft Δt 20 keer kleiner bij dezelfde
snelheid. Maar de gemiddelde snelheid blijft gelijk.
Uit s = vgem t volgt dan dat s 20 keer kleiner wordt.
Conclusie 2: De pootjes van een vlo kunnen ongeveer 2 mm uitstrekken.
2.3 Vallen
26 a Het deel waarbij de parachute nog niet open is.
b Voor een parachutist is het een val zonder parachute, voor een natuurkundige een val zonder luchtweerstand.
27
pulsje
28 a De maan heeft geen dampkring, er is dus geen
luchtweerstand.
b Binas tabel ‘Planetenstelsel’: gmaan = 1,63 m/s2. Dat is
zes keer zo weinig als op aarde.
c De snelheid is het grootst op aarde zonder lucht, want
de versnelling is op aarde veel groter dan op de maan.
20
242759_NAT 3E TF HAVO 4 UW_CH02.indd 20
t
Bij een vrije val is het hellinggetal gelijk aan de
valversnelling, dat is op aarde veel groter dan op de
maan. Het allereerste stukje van een valbeweging
met lucht heeft dezelfde versnelling als de vrije val.
29 a 14,7 m/s
Δv → 9,81 = ___
Δv
g = ___
1,5 dus Δv = 1,5 × 9,81 = 15 m/s.
Δt
dat kan ook met een tabel:
snelheidstoename in m/s
9,81
14,7
tijd in s
1
1,5
Omdat de beginsnelheid nul is, is de snelheid dan
15 m/s.
b 89 m
vgem is dan 7,36 m/s, dus s = vgem t = 7,36 × 1,5 = 11 m.
Dus is het 100 – 11 = 89 m boven de grond.
c Elke seconde neemt de snelheid met 9,81 m/s toe.
Dus één seconde later is de snelheid 14,7 + 9,81 =
24,5 m/s, en nog een seconde later 34,3 m/s.
d 3,1 s
30
30
Δv → 9,81 = ___
g = ___
dus Δt = ____ = 3,1 s
Δt
Δt
9,81
ook dat kan met een tabel:
snelheidstoename in m/s
9,81
30
tijd in s
1
3,06
e 54 m
vgem is dan 15 m/s, dus s = vgem t = 15 × 3,06 = 45,9 m.
Dus is het 100 – 45,9 = 54,1 m boven de grond.
f Na 4,5 s is de snelheid 44,1 m/s
Δv of met een tabel),
(met g = ___
Δt
dan is de gemiddelde snelheid 22,1 m/s,
dus s = vgem t = 22,1 × 4,5 = 99 m
Dus nog nét niet; als de hoogte precies 100,0 m is dan
is hij pas na 4,515 s op de grond.
30 a 5,4 cm
Op de foto is dat 7,5 mm; de golfbal is op de foto
6,0 mm groot, in werkelijkheid is dat 43 mm.
Daarmee kun je de werkelijke afstand bepalen:
afmeting op de foto in mm
6
7,5
werkelijke afmeting in mm
43
54
Door druktechnische redenen kunnen deze uitkomsten een beetje afwijken.
© Noordhoff Uitgevers bv
15/07/13 5:59 PM
Hoofdstuk 2 Bewegen en rekenen
afmeting op de foto in mm
6
28
63
werkelijke afmeting in mm
43
201
452
c De tijd tussen twee flitsen is 1/20 s = 0,05 s.
Dus de tweede flits komt na 2 × 0,05 s = 0,1 s,
de vierde flits na 0,2 s, de zesde na 0,3 s.
d/e
tijd in s
afstand in m vgem in m/s
0
0
-
0,1
0,054
0,54
0,2
0,201
1,05
0,3
0,452
1,51
f Ja: de gemiddelde snelheid neemt in vrijwel even
grote stappen toe, dan moet de snelheid ook
gelijkmatig toenemen.
Besef dat de uitkomsten eigenlijk slechts 2 significante
cijfers hebben, dus dat de onnauwkeurigheid zeker
0,1 m/s is.
g 3,0 m/s
De beginsnelheid is nul, de gemiddelde snelheid
1,5 m/s, dan moet de eindsnelheid dus 3,0 m/s zijn.
3,0
Δv = ___
= 10 m/s2
h g = ___
Δt 0,3
i 10 m/s2
v in m/s
3,5
t
d 27,2 m/s2
Bij het afremmen in het net is de beginsnelheid
9,9 m/s en de eindsnelheid nul.
1 vbegin = 9,9 m/s en veind = 0
2 vgem = 4,95 m/s en Δv = 9,9 m/s.
3 omdat de verplaatsing gegeven is kun je nu de
tijd uitrekenen met s = vgem t
1,8
1,8 = 4,95 × t → t = ____
4,95 = 0,3636 s
9,9
Δv = _______
= 27 m/s2
en de vertraging met: g = ___
Δt 0,3636
32 a 1 vbegin = 0 m/s en veind = 4,7 m/s
2 vgem = 2,35 m/s en Δv = 4,7 m/s.
3 omdat de verplaatsing gegeven is kun je de tijd
uitrekenen met s = vgem t
3,0
3,0 = 2,35 × t → t = ____
2,35 = 1,28 s
4,7
Δv = ____
en dan de vertraging: g = ___
= 3,7 m/s2
Δt 1,28
b Volgens de tabel ‘Planetenstelsel’ in Binas is de
valversnelling 3,7 m/s2, dat klopt dus.
3
2,5
33 a Eerst een val met luchtweerstand, waarbij de
snelheid steeds langzamer toeneemt tot een
maximum, en dan weer langzaam afneemt.
Dan (na het openen van de parachute) in korte tijd
een forse snelheidsafname tot de snelheid weer
constant is:
2
1,5
1
v
0,5
0
het vallen (vgem is in beide gevallen hetzelfde,
namelijk 4,95 m/s):
v
b Op de foto meet je 28 mm resp. 63 mm, in werkelijkheid is dat dus 201 en 452 mm:
0
0,05 0,1 0,15 0,2 0,25 0,3 0,35
t in s
De versnelling is het hellinggetal van de snelheids
3,1
Δv ___
grafiek: g = __
= 0,3 = 10,3 m/s2
Δt
Deze uitkomst lijkt nauwkeuriger, maar gezien het
feit dat de meetpunten al niet zuiver op een lijn
liggen is dat schijn en kunnen we beter opschrijven:
g = 10 m/s2.
31 a Net als bij 29d met de formule of tabel: 1,01 s.
Je kunt zó wel zien dat het net iets meer dan één
seconde moet zijn.
b 5,0 m
Beginsnelheid nul, eindsnelheid 9,9 m/s, dus
vgem = 4,95 m/s;
dan is de verplaatsing van de koorddanser:
s = vgem t = 4,95 × 1,01 = 5,0 m.
c Tijdens het afremmen is de verplaatsing minder dan
tijdens de val; het afremmen duurt dus korter dan
© Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_CH02.indd 21
t
b 37,9 m/s
De totale tijd is 825 seconde, dus
31300
Δx = ______
= 37,9 m/s (= 137 km/h)
vgem = ___
Δt
825
c Zolang de parachute nog niet open is noemen
parachutisten de beweging een vrije val.
d De lucht wordt steeds minder ijl naarmate hij
dichter bij de grond komt, daardoor neemt de
luchtweerstand toe.
e 2,3 m/s2
Δv = 988 km/h = 274,4 m/s, dus
274,4
Δv = _____
2
agem = ___
120 = 2,287 = 2,3 m/s
Δt
21
15/07/13 12:31 PM
Hoofdstuk 2 Bewegen en rekenen
0,50
Δx = _____
= 1,56 m/s
b vgem = ___
Δt 0,32
f 16 km
__
1
1
vgem = __
2 (vbegin + veind) = 2 (0+27,4) = 137,2 m/s
omdat vbegin nul is, moet veind het dubbele zijn van
vgem, dus 3,13 m/s, en Δv is ook 3,13 m/s
dus s = vgem t = 137,2 × 120 = 16464 m = 16 km
3,13,
Δv = ____
dus a = ___
= 9,77 m/s2 = 9,8 m/s2
Δt 0,32
g 9,7 m/s
tussen het openen van de parachute en de landing
zit 9 min 7 s = 547 s;
in die tijd legt hij 5,3 km af met vrijwel constante
snelheid:
c 4,9 × 0,442 = 0,95 m is ongeveer 1 m
4,9 × 0,562 = 1,54 m is ongeveer 1,5 m
d De hoogte waarop hij de sneeuwbal loslaat (t.o.v.
het ijs), hoe lang Madeleine is, en haar snelheid.
e - Hoe ver de bal moet vallen tot het hoofd van
Madeleine: het verschil tussen de hoogte waarop
hij de bal loslaat en haar lengte.
- Hoe lang de bal daarover doet: met de door hem
gevonden formule h = 4,9t2.
- Hoeveel meter Madeleine schaatst in die tijd, met
s=v·t
5300
Δx = _____
vgem = ___
547 = 9,7 m/s (= 35 km/h)
Δt
dat is dus ook de landingssnelheid; je kunt dat niet
precies zeggen omdat de snelheid niet helemaal
constant is.
In het begin is de snelheid veel groter en remt hij sterk
af, maar in verhouding tot die 547 seconden duurt dat
maar heel even
h 7091 m
_______
v 1343/3,6
t = __
g = 9,813 = 38 s
1343
s = vgem t = ______ × 38 = 7091 m
2 × 3,6
i De luchtweerstand is de beperkende factor voor de
topsnelheid. Hoe hoger je bent, hoe minder last je
hebt van luchtweerstand, vanwege ijlere lucht.
34 a 0,96 s
de snelheid neemt toe van 0 tot 25 m/s,
dus vgem = 12,5 m/s
12 dus Δt = ____
12
Δx → 12,5 = ___
vgem = ___
12,5 = 0,96 s
Δt
Δt
b 26 m/s2
25
Δv = _____
= 26 m/s2
a = ___
Δt 0,96
(Dit is 26/9,81 = 2,7g, met de normale valversnelling
erbij voel je 3,7g.)
c 2,6 s
in het hoogste punt is de snelheid weer nul, dus Δv
is dan 25 m/s
25
25
Δv → 9,8 = ___
a = ___
dus Δt = ___ = 2,6 s
Δt
Δt
9,8
d 44 meter
tijdens het afschieten ga je 12 m omhoog,
tijdens het vertragen is vgem ook 12,5 m/s:
s = vgem t = 12,5 × 2,55 = 31,9 m
dus totaal 12 + 31,9 = 44 m
e 11 m
na 2,6 s vallen is de snelheid 2,6 × 9,81 = 25,5 m/s,
omdat de beginsnelheid nul was is de gemiddelde
snelheid 12,75 m/s:
s = vgem t = 12,75 × 2,6 = 33,2 m
je bent dan nog 43,9 – 33,2 = 11 m boven de grond
35 a Het filmpje beeld voor beeld afspelen en tellen
hoeveel beeldjes er zijn vanaf het loslaten tot het
neerkomen. Hij moet dan weten hoeveel beeldjes
per seconde er zijn.
22
242759_NAT 3E TF HAVO 4 UW_CH02.indd 22
36
37
2.4 Videometen
Het aantal beelden per seconde dat de camera
opneemt, en de schaal van de filmbeelden op je
scherm (of op papier).
Computeropdracht
38 a Zonder een schaal kan de computer geen werkelijke
afstanden berekenen voor de grafiek.
b Bij de maximale beeldgrootte (op je beeldscherm)
kun je de uiteinden van de meetlat het nauwkeurigst op de juiste plaats leggen.
39
Hij staat na het starten van de meting nog even stil
en versnelt dan. Op het eind van de meting is de
snelheid vrijwel constant geworden.
40
Dan kan het bestand zo groot worden dat het meetprogramma er niet mee overweg kan of het geheugen
van de computer te klein is. Als je via een netwerk
werkt, kun je ook daar tegen beperkingen oplopen.
41 a avi-formaat, 30 beeldjes per seconde.
b Je filmt dan de hele beweging terwijl je alleen het
remmen nodig hebt. Dan wordt de film veel te lang
en het bestand veel te groot.
c Je gaat op een behoorlijke afstand staan, zó dat je
vrijwel loodrecht kijkt op het deel van de beweging
dat je wilt filmen. Bij een normale camera moet de
afstand waarvandaan je filmt minimaal even groot
zijn als de afstand die je in beeld wilt hebben. Voor
videometen ga je het liefst nog verder staan.
d Je zorgt dat er iets, waarvan je de afmeting precies
weet, duidelijk in beeld is, bijvoorbeeld de fiets zelf
of een meetlat. De laatste moet dan wel op dezelfde
afstand staan of liggen als de fiets.
42 a 4 · 101 m
Het hekje is op de foto 3,6 mm hoog; de hele toren
10,7 cm:
hoogte op foto in mm
3,6
107
werkelijke hoogte in m
1,3
39
© Noordhoff Uitgevers bv
15/07/13 6:29 PM
Hoofdstuk 2 Bewegen en rekenen
Δv → 9,81 = ___
Δv
g = ___
2,4 dus Δv = 2,4 × 9,81 = 23,5 m/s.
Δt
dat kan ook met een tabel:
snelheidstoename in m/s
9,81
23,5
tijd in s
1
2,4
Omdat de beginsnelheid nul is, is de snelheid dan
23,5 = 24 m/s.
e 28 m
vgem is dan 11,8 m/s, dus s = vgem t = 11,8 × 2,4 = 28 m.
f 27,7 m/s2
Je wordt afgeremd van 23,5 m/s tot nul over een
afstand van 10 meter.
Dus Δv = −23,5 m/s en vgem is de helft van 23,5 m/s,
dus 11,8 m/s
10 → Δt = ____
10 = 0,85 s
Δx → 11,8 = ___
vgem = ___
Δt
Δt
11,8
−23,5
Δv = _____
dan is a = ___
= −27,7 m/s2
Δt 0,85
g 72 beeldjes
in 2,4 seconde neemt hij 30 × 2,4 = 72 beeldjes op.
h Ja: de valbeweging verloopt vloeiend en heeft geen
snelle veranderingen; daarvoor heb je geen 72
meetpunten nodig om een goede grafiek te krijgen.
Zelfs met één op drie beeldjes krijg je nog een
redelijke grafiek.
Eigenlijk moet je kijken waar de beweging het snelst
verandert. Je moet zó veel beeldjes gebruiken dat ook
de snelste verandering nog uit meerdere meetpunten
bestaat.
43
pulsje
44 a Te groot, want het echte balletje krijgt meer
snelheid dan berekend met het model, dus volgens
het model is de luchtweerstand te groot.
b 2,5 m/s
Teken een raaklijn aan de groene plaatsgrafiek
op het tijdstip t = 0,3 s en bepaal daarvan het
2,15 – 0
Δx = ________
hellinggetal: ___
= 2,5 m/s
Δt 1,0 – 0,14
(Een afwijking van 0,1 à 0,2 m/s in de uitkomst is
acceptabel)
© Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_CH02.indd 23
gemeten afstand in m
afstand volgens model
2,4
2,2
2,0
1,8
1,6
1,4
1,2
1,0
0,8
0,6
0,4
0,2
0
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0
tijd in s
c Volgens de snelheidsgrafiek komt er 2,5 m/s uit, dus
dat klopt.
d Bij een vrije val is na 0,3 s de snelheid 0,3 × 9,81 =
Δv
2,9 m/s (met verhoudingstabel of met g = __
)
Δt
Dus het is al geen vrije val meer.
Dat kun je ook zien aan de snelheidsgrafiek: die na 0,3
s al niet meer recht.
e 4,4 m/s2
Teken een raaklijn aan de paarse snelheidsgrafiek op
het tijdstip t = 0,3 s en bepaal daarvan het
– 1,0
Δv 5,0
2
hellinggetal: __
= _____
0,9 = 4,4 m/s
Δt
(Een afwijking van 0,2 à 0,3 m/s2 in de uitkomst is
acceptabel)
5,0
gemeten snelheid in m/s
snelheid volgens model
Vanwege de relatieve onnauwkeurigheid van de
hoogte van het hekje is het beter om af te ronden
op één cijfer.
b Iets te klein
De bovenkant van de toren is verder weg en komt
dus wat kleiner op de foto. Alles wat je daar meet is
dus iets groter dan het lijkt.
Je kunt ook zeggen: als het hekje boven in de toren had
gezeten dan was het iets kleiner geweest op de foto.
Je kunt schatten hoe groot de afwijking is door te
meten hoe breed de toren onderaan en bovenaan op
de foto is, of door de afstand tussen de dwarsstangen
in de toren onder en boven te meten. Je ziet dan dat
de afwijking ruwweg 10% is.
c De toren is dus hoger.
d 24 m/s
4,5
4,0
3,5
3,0
2,5
2,0
1,5
1,0
0,5
0
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0
tijd in s
f Volgens het rekenmodel is na 0,3 s de snelheid 2,3
m/s. De vertraging door de luchtweerstand is
kv2 = 1 × 2,32 = 5,3 m/s2.
De versnelling is dan 9,81 – 5,3 = 4,5 m/s2, dat klopt
goed met de uitkomst bij vraag e.
g 3,1 m/s
Als de snelheid constant is geworden is de versnelling nul, dus dan is kv2 gelijk aan de valversnelling.
Met k = 1,0 is dan v2 = 9,81, dus v = 3,1 m/s.
2.5 Nauwkeurig meten en rekenen
45 a De verschillen groter dan 0,01 s ontstaan doordat je
niet steeds op precies het juiste moment de
stopwatch aan- en uitzet.
Je noemt dit ook wel de invloed van je reactietijd.
23
15/07/13 6:00 PM
Hoofdstuk 2 Bewegen en rekenen
b Als je de slinger tien maal heen en weer laat
slingeren voordat je de stopwatch stil zet krijg je
maar één keer een start- en een stopafwijking op
tien slingeringen. Per slingering wordt je afwijking
dus gemiddeld tien keer zo klein.
46 a Het gemiddelde van groep A is
7,443 + 7,366 + 7,405 + 7,451 + 7,392
________________________________
5
= 7,4114
met een gemiddelde afwijking van
0,0316 + 0,0454 + 0,0064 + 0,0396 + 0,0194
________________________________________
0,02848 = 0,03.
5
=
De uitkomst is dus 7,41 ± 0,03 m
Aan de gemiddelde afwijking zie je dat de tweede
decimaal, de 1, niet zeker is. Daarom geef je niet meer
dan 2 decimalen op. Je rondt de gemiddelde afwijking
0,02848 dus ook af op 0,03.
b Het gemiddelde van groep B is
7,49 + 7,45 + 7,48 + 7,46 + 7,50
____________________________
5
= 7,476
met een gemiddelde afwijking van
0,014 + 0,026 + 0,004 + 0,016 + 0,024
___________________________________
= 0,0168 =
5
0,02
De uitkomst is dus 7,48 ± 0,02 m
c Groep A heeft het nauwkeurigste meetlint gebruikt,
want zij hebben in mm gemeten en groep B in cm.
d Nee, groep B heeft het nauwkeurigst gemeten,
want de gemiddelde afwijking (0,02 m) is kleiner
dan die van groep A (0,03 m).
e Achterin
De breedte voorin (groep A) ligt tussen 7,38 en 7,44 m
en achterin (groep B) tussen 7,46 en 7,50 m.
47 a 1012 bytes
In Binas kun je onder ‘Vermenigvuldigings-factoren’
of ‘Voorvoegsels’ vinden dat T staat voor ‘tera’, of
1012.
Eigenlijk rekenen ze in de informatica anders: het
voorvoegsel ‘kilo’ betekent 210 = 1024; ‘mega’ betekent
10242, ‘giga’ is 10243 en ‘tera’ staat voor 10244 =
1,1 · 1012 byte. Er zijn voorstellen om de notatie te
veranderen want de afwijking wordt bij grotere
schijven procentueel steeds groter.
b 1 miljoen
‘micro’ betekent 10−6 = één miljoenste
48
Misschien krijg je twee verschillende uitkomsten.
Met gebruik van de ^ - toets kom je dan op een
uitkomst van 1 · 10−5 en met de EE- of EXP-toets krijg
je 1 · 105.
De tweede uitkomst is goed. Voor een correcte
uitkomst moet je bij de eerste manier invoeren:
8,7 : (8,7 × 10 ^ −5). Je had dus ook nog haakjes om
de noemer moeten zetten.
24
242759_NAT 3E TF HAVO 4 UW_CH02.indd 24
49 a
b
c
d
e
f
g
h
i
j
1,23 · 102
2 · 10−1
9,87 · 10−5
2,1 · 104
4,1 · 10−5
1,1 · 104
2,13 · 10−4
8,3 · 10−8 s
4,1 · 1012 g = 4,1 · 109 kg
5,0 · 10−4
50 a 10,06 ........................... 4
4,2 ................................ 2
100000 ....................... 6
1,04 · 10−6 .................... 3
0,0006 ....................... 1
1,000006 · 108 ........... 7
Nullen vooraf en machten van 10 tellen niet mee!
b 1,000006 · 108; 100000; 10,06; 1,04 · 10−6; 4,2; en
0,0006.
Hoe meer significante cijfers, hoe nauwkeuriger.
c 1,000006 · 108; 1,00000 · 105; 1,006 · 101; 1,04 · 10−6;
4,2; 6 · 10−4
220 = 1,654 m/s
51 a ____
113
210 = 1,567 m/s
b ____
134
c In tiende m/s
De afstand is in 0,01 km (dus op 10 m) nauwkeurig
gemeten, de tijd in seconde. Als je de afstand 0,01 km
verandert dan zie je dat de gemiddelde snelheid al
0,1 m/s verandert.
De tijdmeting heeft minder invloed omdat die naar
verhouding nauwkeuriger is gemeten dan de afstand.
52 a Nee: de waarde is wel hetzelfde, maar de nauwkeurigheid niet. ‘0,5 m’ is in decimeter nauwkeurig
gemeten, '50 cm’ in centimeter nauwkeurig.
b Dan moet de uitkomst evenveel significante cijfers
hebben als de meetwaarde met de minste significante cijfers.
0,5 × 0,50 = 0,25 = 0,3
c Dan moet de uitkomst evenveel cijfers achter de
komma hebben als de meetwaarde met de minste
cijfers achter de komma.
0,5 + 0,50 = 1,0
53 a
b
c
d
e
f
g
h
i
j
5
één significant cijfer
1119
nul cijfers achter de komma
1,0 · 102
2 significante cijfers
5,0
2 significante cijfers
0,2
één significant cijfer
6,1
één cijfer achter de komma
4 · 103
één significant cijfer
11
één cijfer achter de komma
3 · 101
één significant cijfer
4,7 · 103
684 = 0,684 · 103, dan optellen en dan
maar één cijfer achter de komma.
© Noordhoff Uitgevers bv
15/07/13 6:02 PM
Hoofdstuk 2 Bewegen en rekenen
27,2
pulsje
55
Stap 1: schetsen, verzamelen, verkennen,
stap 2: aanpak verzinnen,
stap 3: plan uitvoeren,
stap 4: alles in orde?
56
Stap 1: onderzoek arm, röntgenfoto maken, is er nog
ander letsel?
Stap 2: behandeling vaststellen: bijvoorbeeld: eerst
de gebroken botten rechtzetten en dan gips er
omheen.
Stap 3: behandeling uitvoeren.
Stap 4: na uitharden gips controleren of het goed zit
en of het bot goed zit (d.m.v. röntgenfoto).
13,6
vgem
0
7
8
Toepassing
t
27,2
Δv = ____
= 108,8 = 1,1 · 102 m/s2
a = ___
Δt 0,25
Dan heeft hij dubbel zo veel tijd, dus hoeft de
gemiddelde snelheid maar half zo groot te zijn om
de gewenste afstand af te leggen. Dan is de eindsnelheid ook maar half zo groot (zie vraag 6).
Als de eindsnelheid de helft is en de tijd het dubbele, dan is de versnelling vier keer zo klein.
v
Opgave 1 De penalty
1 a Volgens de tabel ‘Eenheden’:
1 voet = 0,3048 m
1 yard = 0,9144 m
b 1 yard = 3 voet
c 8 yard : 8 voet is dus 3 : 1
d 12 yard = 12 × 0,9144 m = 1,097 m = 11 m
2
veind
v in m/s
54
1
2
Het doel is 8,0 yard = 7,315 m breed; 0,25 m van de
paal is dus (_21 × 7,315) – 0,25 = 3,41 m uit het midden:
t
De oppervlakte onder de twee grafieken is hetzelfde,
maar het hellingsgetal van grafiek 2 is vier keer zo
klein.
7,315 m
3,41 m
9
Als je de baan van de bal verdeelt in twee stukken
van 10,5 m en 1,0 m, en dan twee keer Pythagoras
toepast met de gegeven 3,25 m, dan klopt het.
3,4 m
11,0 m
11,5 m
3,2
5m
1,0 m
11,0 m
stip
10,5 m
Pythagoras:
112 + 3,412 = 132,6 dus de schuine zijde is
_____
132,6 = 11,5 m
3
Volgens diverse bronnen kan 160 km/h wel gehaald
worden, dat is 44 m/s; over 11 m doet de bal dan
0,25 s.
4
0,25 – 0,15 = 0,10 s
5
3,4
Δx = ____
= 13,6 = 14 m/s
vgem = ___
Δt 0,25
6
10,52 + 3,252 = 11,02 en 3,252 + 1,02 = 3,42
NB: Bovenstaande tekening is niet op schaal!
Als je de grote driehoek netjes op schaal tekent en
dan de loodlijn trekt kun je ook nameten dat het
klopt.
Hoe groter de tekening, des te nauwkeuriger!
Als de beginsnelheid nul is en het gemiddelde
13,6 m/s, dan moet de eindsnelheid 27,2 = 27 m/s zijn.
© Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_CH02.indd 25
25
15/07/13 12:31 PM
Hoofdstuk 2 Bewegen en rekenen
50
20
3 · 10 m/s
2
2
20
10
0
10
vgem
17
0
t
Als de bal afremt van 20 m/s tot nul dan is de
gemiddelde snelheid 10 m/s; de tijd over 0,6 m is
dan 0,06 s, dus
20 = 333 = 3 · 102 m/s2
Δv = _____
a = ___
Δt 0,06
38
Δv = ___
agem = ___
= 7,45 = 7,5 m/s2
Δt 5,1
15
16
Door toenemende luchtweerstand zou de versnelling steeds verder afnemen en op het laatst nul
worden. De grafiek zou steeds minder steil gaan
lopen en uiteindelijk horizontaal worden.
6,7 m/s2
Teken een raaklijn aan de grafiek bij t = 3,0 s en
bepaal daarvan het hellingsgetal; als het goed is
komt daar ongeveer 6,7 m/s2 uit (± 0,2 m/s2)
2
3
4
5
t in s
6
Dan zou de grafiek recht zijn met een helling van
9,8 m/s2. (gewoon het eerste stukje recht door
trekken)
v in m/s
40
20
10
3,0 s
Δv = 15,2 – 0,3 = 14,9 m/s; a = 5 m/s2,
Opgave 3 Valtoren
14 7,5 m/s2
Δv en Δt aflezen en dan:
1
30
29,4
Δv = ____
= 8,8 m/s2
a = ___
Δt 3,33
Δv = wordt dan
a = ___
Δt
14,9
5,0 = ____ → Δt = 2,98 = 3,0 s
Δt
0
50
Opgave 2 Goliath
12
8,8 m/s2
106 km/h = 29,4 m/s
dus vgem = 14,7 m/s
over 49 m doet hij dan 3,33 s, dus
13
40
30
v in m/s
11
De afstand die de bal moet afleggen wordt 8,7%
kleiner, de afstand die de keeper moet afleggen
wordt maar 4,4% kleiner, dus naar verhouding moet
de keeper nu meer afleggen dan de bal.
Bovendien heeft de bal een constante snelheid en
beweegt de keeper versneld: hij heeft op het eind
de meeste snelheid. Iets minder afstand levert
daardoor nauwelijks tijdwinst op.
v in m/s
10
0
0
1
2
3
4
5
t in s
6
18
2,83 s
100 km/h = 27,77… m/s
27,78
Δv wordt dan 9,81 = _____
→ Δt = 2,83 s
g = ___
Δt
Δt
19
71 m
vgem is dan 50 km/h = 13,88.. m/s,
dus s = vgem t = 13,89 × 2,83 = 39,3 m.
Dus is hij 110 – 39,3 = 71 m boven de grond.
20
9,7g
Hij komt neer met 38 m/s en wordt afgeremd tot
stilstand, dus Δv = 38 m/s
38
Δv = ___
= 95 m/s2 dat is 9,7g
agem = ___
Δt 0,4
(Hetgene wat je zou voelen als je de vloeistof uit het
experiment was, is 10,7g, omdat de normale alversnelling er ook nog altijd is. Als je stil zit voel je al 1g.)
Opgave 4 Op tijd stoppen
21
13 m
30 km/h = 8,33... m/s
in 0,7 s rijdt hij dus nog 8,33 × 0,7 = 5,83 m.
tijdens het afremmen:
8,33
Δv wordt 5,2 = ____
→ Δt = 1,60 s
a = ___
Δt
Δt
26
242759_NAT 3E TF HAVO 4 UW_CH02.indd 26
© Noordhoff Uitgevers bv
15/07/13 12:31 PM
Hoofdstuk 2 Bewegen en rekenen
22
v
de gemiddelde snelheid is dan 15 km/h =
4,166… m/s,
dus s = vgem t = 4,167 × 1,60 = 6,68 = 6,7 m
stopafstand = reactie-afstand + remafstand =
5,83 + 6,68 = 12,51 = 13 m
28 m
50 km/h = 13,88... m/s
in 0,7 s rijdt hij dus nog 13,89 × 0,7 = 9,7 m
tijdens het afremmen:
v
0,7
13,89
Δv wordt 5,2 = _____
→ Δt = 2,67 s
a = ___
Δt
Δt
II
∆t
t
De oppervlakte onder de snelheidsgrafiek moet
11,17 m zijn.
De oppervlakte onder de rechthoek (I) is 0,7 × v; de
oppervlakte onder de driehoek (II) is _21 × Δt × v
Omdat de helling nog steeds −5,2 m/s2 is weet je dat
v
de remtijd Δt gelijk is aan ___
5,2
de gemiddelde snelheid dan 25 km/h = 6,94… m/s,
dus s = vgem t = 6,944 × 2,67 = 18,5 m
stopafstand = reactie-afstand + remafstand =
9,7 + 18,5 = 28,2 = 28 m
5
dat is 2,3 keer zo groot, en niet _3 = 1,7 keer zo groot.
Als je dat invult is oppervlakte II gelijk aan:
23
___
v
____
v2
2 × 5,2 × v = 10,4
v in m/s
__
1
5
0
(
)
Voor de stopafstand geldt dan:
v2
Opp. I + opp. II = 0,7 × v + ____
10,4 = 11,17
Als je de formule voor de oppervlakte schrijft in de
vorm:
____
v2
2
10,4 + 0,7v − 11,17 = 0,096v + 0,7v − 11,17 = 0
dan kun je de oplossing vinden met de abc-formule.
v = 7,74 ,/s
10
0
1
2
3
t in s
24
1,7 m
Hij rijdt 0,20 s langer door met een snelheid van 8,33
m/s, dus 0,20 × 8,33 = 1,7 m
25
1,3 m
De vertraging is 1,25 × 5,2 = 6,5 m/s2. Op dezelfde
manier als bij vraag 21 en 22 kun je uitrekenen dat de
remtijd Δt dan 1,28 s is, en de remafstand 5,34 m. Bij
vraag 21 was de remafstand 6,68 m, nu is die dus 1,3 m
korter.
De ‘reactie-afstand’ is niet veranderd.
26
I
7,7 m/s (= 28 km/h)
Als de remvertraging 20% kleiner is dan bij vraag 25,
dan is hij weer 5,2 m/s2.
De remafstand moet 5,34 m zijn en de ‘reactieafstand’ is nog steeds 5,83 m (zie vraag 21). Dus de
stopafstand is 11,17 m.
Deze vraag is lastig omdat je de snelheid niet weet,
en daardoor ook niet de remtijd.
© Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_CH02.indd 27
Opgave 5 Nauwkeurigheid
27 31 km/h; 0,8 s en 4,7 m/s2
Je gebruikt dan de grootste snelheid en reactietijd
en de kleinste remvertraging die mogelijk zijn
binnen de gegeven marges.
28
15 m
Dezelfde berekening als bij vraag 21, met:
Δv = 31 km/h = 8,61 m/s, daaruit volgt dat
Δt = 1,83 s, vgem = 4,31 m/s en de remafstand 7,9 m;
de reactie-afstand is 8,6 × 0,8 = 6,9 m;
dus de stopafstand 6,9 + 7,9 = 15 m
29
11 m
Nu reken je met 29 km/h = 8,06 m/s, 0,6 s reactietijd en 5,7 m/s2 remvertraging.
Dat geeft Δt = 1,41 s, vgem = 4,03 m/s dus de remafstand is 5,7 m; de reactie-afstand is 4,8 m;
dus de stopafstand is 4,8 + 5,7 = 11 m
30
13 ± 2 m
Bij de gegeven onzekerheden kan de stopafstand
wel 2 m afwijken van de bij vraag 21 berekende
waarde.
Volgens de regels hebben we die uitkomst afgerond
op 2 significante cijfers: 13 m
Dat betekent dat de stopafstand in meter nauwkeurig is bepaald; dat is in overeenstemming met de
gevonden onzekerheid van 2 m.
27
15/07/13 12:31 PM
Hoofdstuk 2 Bewegen en rekenen
Opgave 6 Reactietijd meten
31
A: 2: je weet dat je klasgenoot iets gaat doen
waarop jij moet reageren
B: 3: je ziet de sprinter op de finish af gaan
C: 1: dit komt volkomen onverwacht
32
40
0,7 + 0,5 + 0,6 + 0,7 + 1,0
_______________________
5
0,0 + 0,2 + 0,1 + 0,0 + 0,3
_______________________
5
2,45
tijd in s
1
0,25
Omdat de beginsnelheid nul is, is de snelheid dan
2,45 m/s.
vgem is dan 1,23 m/s, dus s = vgem t = 1,23 × 0,25 =
0,306 m.
33
s = 4,9 t2 = 4,9 × 0,252 = 0,306 m
34
0,23 s
s = 4,9 t2 wordt 0,26 = 4,9 × t2
t2 = 0,053 dus t = 0,23 s
35
Opgave 7 Bad te klein
41 5 cijfers
De gegeven lengte is 24,996 meter.
42
0,05
afstand in cm 1,2
43
0,10
0,15
0,20
0,25
4,9
11,0
19,6
30,7
36
Omdat de valbeweging versneld is.
Je kunt ook zeggen: in de formule zit een kwadraat,
dus de afstand is niet recht evenredig met de tijd.
37
0,2 m
In de formule 0,2 s invullen; zie ook de tabel bij
vraag 34.
39
0,16 s
s = 4,9 t2 wordt 0,127 = 4,9 × t2
t2 = 0,0259 dus t = 0,16 s
Het gemiddelde is
0,4 + 0,6 + 0,6 + 0,9 + 0,5
________________________
5
= 0,60 s
met een gemiddelde afwijking van
0,2 + 0,0 + 0,0 + 0,3 + 0,1
_______________________
= 0,12 s
5
De uitkomst is dus 0,6 ± 0,1 s
28
242759_NAT 3E TF HAVO 4 UW_CH02.indd 28
0,03369 s
Volgens de tabel ‘Geluid - Voortplantingssnelheden’
in Binas is bij 293 K de geluidssnelheid in water 1,484
· 103 ms−1 = 1484 m/s.
De afstand is 2 × 24,996 = 49,992 m
afstand in m
1484
49,992
tijd in s
1
0,03369
Omdat de afstand in 5 en de snelheid in 4
significante cijfers is gegeven, mag je de uitkomst
ook in 4 cijfers geven.
Op de strook zet je een nulstreep en vervolgens op
1,2 cm ‘0,05 s’, op 4,9 cm ‘0,10 s’, enzovoorts.
38
0,016 %
4 mm = 0,004 m op de 25 m,
0,004
dus ______
25 × 100% = 0,016%
Met de formule reken je uit hoe ver de liniaal
gevallen is na bijvoorbeeld 0,05 s: 0,10 s; 0,15 s;
0,20 s etc. Het is handig die afstanden om te
rekenen naar centimeter. Zie de tabel hieronder:
tijd in s
= 0,12 s
De uitkomst is dus 0,7 ± 0,1 s
Je kunt niet zeggen dat de reactietijd groter is
geworden want het verschil tussen de twee uitkomsten is net zo groot als de onzekerheid.
dat kan ook met een tabel:
9,81
= 0,70 s
met een gemiddelde afwijking van
0,31 m
Δv
Δv → 9,81 =____
g = ___
0,25 dus Δv = 0,25 × 9,81 = 2,45 m/s.
Δt
snelheidstoename in m/s
Het gemiddelde is
44
45
In 10−6 s nauwkeurig
Je moet de afstand ‘heen-en-terug’ dan op 2 mm
nauwkeurig kunnen meten; over die afstand doet
het geluid 1,35 · 10−6 s; je moet dus in miljoensten
van seconden kunnen meten.
afstand in m
1484
0,002
tijd in s
1
1,35∙10-6
In 3 · 10−4 graad nauwkeurig
Je moet eerst een schatting maken hoeveel de
geluidssnelheid verandert per graad temperatuurstijging of -daling. Uit de tabel in Binas blijkt dat de
geluidssnelheid 81 m/s afneemt als de temperatuur
20 graden daalt, maar slechts 45 m/s toeneemt als
de temperatuur 20 graden stijgt. Het gemiddelde
daarvan is 63 m/s snelheidsverandering per 20
graden, dat is 3,2 m/s per graad.
Om de snelheid in 0,001 m/s nauwkeurig te kunnen
meten moet de temperatuur op 0,0003 graad
nauwkeurig bekend zijn:
temperatuurverandering in
graden
20
1
0,0003
snelheidsverandering in
m/s
63
3,2
0,001
© Noordhoff Uitgevers bv
15/07/13 12:31 PM
Hoofdstuk 2 Bewegen en rekenen
46
3
1,7046 m/s
Zonder luchtweerstand hebben ze steeds dezelfde
versnelling. De eerste gaat dus voortdurend sneller
dan de tweede (en de afstand wordt steeds
groter...). Je kunt zelf bepalen of je veel of weinig
luchtweerstand hebt, door je houding aan te
passen.
1500,0
vgem = ______ = 1,7046 m/s
879,97
De lengte van een 25-meter bad moet op de
millimeter kloppen; 1500 m is 60 baantjes, dus die
afstand heeft een afwijking van hoogstens 60 mm =
0,06 m. Je mag dus zeggen dat de afstand
1500,0 meter is.
14 minuten en 39,97 s = 879,97 s.
Zowel de afstand als de tijd hebben 5 significante
cijfers, dus de gemiddelde snelheid ook.
47
0,14 s
Dan had hij 60 × 4 mm = 0,24 m minder gezwommen met een snelheid van 1,7046 m/s.
afstand in m
1,7046
0, 24
tijd in s
1
0,14
Korter: Hij zou 0,016 % van 879,97 s = 0,14 s gewonnen hebben. (zie vraag 42)
Proefwerkopgaven
1 a 5 km
15,4
15,4 min = ____ = 0,257 uur, dus de tijd is 1,257 uur
60
s = vgem t = 4 × 1,257 = 5,027 = 5 km.
Je kunt ook de snelheid omrekenen naar m/s en de
tijd in seconden, maar dat is veel meer werk.
b 1 m/s
Haar tijd is 1 h en 10,4 min = 4224 s
5027
vgem = _____
4224 = 1,19 = 1 m/s (4 km/h)
2 a 2,9 m/s2
De versnelling op een tijdstip bepaal je met een
raaklijn:
16 = 2,9 m/s2
Δv = ___
a = ___
Δt 5,6
Dit gaat niet erg nauwkeurig; een afwijking van
0,2 m/s2 is acceptabel.
b 16 meter
De snelheid neemt toe van ongeveer 5,5 m/s tot
10 m/s; het gemiddelde daarvan is 7,8 m/s.
s = vgem t = 7,8 × 2 = 16 meter
Ook dit is niet erg nauwkeurig te bepalen.
c 33 m
Hier moet je de kromme vervangen door een rechte
lijn zoals in bron 12 van hoofdstuk 1. Na vijf seconden
is de snelheid dan 13 m/s, dus de gemiddelde
snelheid ongeveer 6,5 m/s.
s = vgem t = 6,5 × 5 = 33 meter
d 39 s
Hij rijdt 500 – 55 = 445 m met een constante
snelheid van 14 m/s; dat duurt 31,8 s.
De totale tijd is dus 7 + 31,8 = 38,8 = 39 s.
e 34 m
Stefan ligt na 7 seconden al 5 meter voor, en moet
dan nog 440 m met een snelheid van 15 m/s; dat
duurt 29,3 s. Hij schaatst dus 29,3 s met een relatieve
snelheid van 1 m/s t.o.v. Wouter, en legt dus 29,3 m
meer af dan Wouter.
Hij ligt dus 29,3 + 5 = 34 m voor.
© Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_CH02.indd 29
4 a 120 km/h = 33,33 m/s
33,33
Δv = _____
2
a = ___
7,4 = 4,5 m/s
Δt
dat klopt met de gegeven versnelling.
b Omdat de beginsnelheid nul is, is de gemiddelde
snelheid 16,67 m/s,
s = vgem t = 16,67 × 7,4 = 123 m dus ze haalt het ruim.
c Hij filmt alleen het eerste stukje loodrecht op de
beweging van de motor. Op het laatste filmt hij
bijna recht van achteren. Om de hele beweging
enigszins van opzij te kunnen filmen zou hij veel
verder weg moeten gaan staan, denk aan 200 m.
5 a 1,35 s
13,2
Δv wordt dan 9,81 = ____
→ Δt = 1,35 s
g = ___
Δt
Δt
b 10,4 m
vbegin = 0, veind = 13,2 m/s dus vgem = 6,6 m/s
s = vgem t = 6,6 × 1,35 = 8,88 m.
Hij is dus 8,9 m gevallen. Omdat het zeil 1,5 m boven de
grond was, is hij dus van 10,4 m hoogte gesprongen.
c 58 m/s2
De snelheidsverandering is 13,2 m/s. De tijd bereken
je met de gemiddelde snelheid:
Hij remt af van 13,2 m/s tot nul, dus ook tijdens het
afremmen is de gemiddelde snelheid 6,6 m/s.
Over 1,5 m doet hij dan 0,227 s.:
13,2
Δv = _____
= 58 m/s2
a = ___
Δt 0,227
(Alternatief: 8,9/1,5 = 5,9g = 58 m/s2)
6 a
b
c
d
e
f
g
3,47 = 3,5
1,548 = 2
16,03 = 16
0,48 = 0,5
256 = 2,6 · 102
4 = 4,0
2,45... = 2,5
29
15/07/13 12:31 PM
Hoofdstuk 3 Elektriciteit
Hoofdstuk 3
Elektriciteit
Introductie
1 a De bliksem ging vanuit de arm naar haar hand.
b De bliksem kwam niet langs vitale organen waardoor het meisje de inslag overleefd heeft.
2
3
De weg die de stroom door het lichaam aflegt, is
bepalend voor de aangerichte schade.
6
Als je het uiteinde van een batterij, via een stroomdraadje tegen je tong houdt, ontstaat er een
prikkeling in je tong als de batterij nog stroom
levert.
Een lichte tinteling voel je bij 0,5 mA (wisselstroom)
en 2 mA (gelijkstroom).
3.1 Lading spanning en stroom
Opgewreven glas is positief geladen. Omdat
perspex afstoot, is het ook positief geladen en heeft
dus een tekort aan elektronen.
2 a Beide zijn opgeladen.
b De lading van de kam springt eerst over naar de
enkele haren, die dan dezelfde lading krijgen als de
kam. En gelijke ladingen stoten elkaar af.
c De lading van de kam springt weer terug naar de
haren, waardoor beide neutraal worden. De kracht
verdwijnt dan.
3 a Elektronen en zijn negatief. Door een extra elektron
krijg je dus een negatief atoom (= ion).
b Dan krijg je een positief atoom.
4
Evenveel plus als minlading, dus ook 10 protonen.
5
Zoveel protonen zouden elkaar sterk af moeten
stoten.
30
242759_NAT 3E TF HAVO 4 UW_CH03.indd 30
–
–
–
– –
–
–
–
–
–
–
+
+
+
+
+
+
–
––
–
–
–
b Elektronen zijn negatief en worden dus afgestoten
door de negatief geladen ballon.
e De afstand tot de positieve kant is kleiner dan de
afstand tot de negatieve kant. Hoe kleiner de
afstand des te groter is de kracht. De aantrekkende
kracht is dus groter dan de afstotende kracht.
De stekker is een adapter. Op de snoer staat dus een
lage spanning, die nauwelijks gevaarlijk is.
5
1
–
Bij de koe gaat de bliksem bij de ene poot naar
binnen en bij de andere poot naar buiten. De poten
bij de koe staan verder uit elkaar dan de benen bij de
boer. Bij de koe gaat de bliksem langs vitale organen
zoals het hart.
2
×1
4 a 0,02 = stroomsterkte
_____
stroomsterkte = 0,02 = 0,14 A
b 0,02 = 0,52 × tijd
tijd = 0,08 s
7
6 a,c,d
7
Houd een opgewreven glazen staaf bij de bol en
onderzoek of deze afgestoten wordt, dan is de bol
positief geladen, anders negatief.
8
Elektronen zijn negatief, een pluspool heeft dus een
te kort aan elektronen.
9
Tussen beide polen van het stopcontact loopt geen
stroom. Kennelijk geleidt lucht de elektrische
stroom niet.
10 a 27 C in 60 s betekent 27/60 = 0,45 A.
b 1 uur is 3600 s. Dus 3600 × 0,0600 = 216 C.
Dat zijn 216 × 6,25 · 1018 = 1,35 · 1021 elektronen.
c 8 C in 1s. Het duurt dus 2500/8 = 312,5 s
= 312,5/60 = 5,2 min.
11 a 2,0 · 10−4 coulomb betekent 2,0 · 10−4 × 6,25 · 1018 =
1,35 · 1015 elektronen.
b De energie is 20 000 J per coulomb. De totale
energie is dan 20 000 × 2,0 · 10−4 = 4,0 J.
12 a De spanning is 1,5 V en de stroomsterkte is 30 mA.
b 0,03 × 2 × 60 = 3,6 C
Dit is 3,6 × 6,25 · 1018 = 2,25 · 1019 elektronen.
c 1,5 J per C. Dus 3,6 × 1,5 = 5,4 J.
13
Het symbool met de twee streepjes is de spanningsbron. Het rondje met de A is de stroomsterktemeter.
Het rondje met de V is de spanningsmeter. Het
rondje met het kruisje is de lamp.
14
De stroomrichting was al afgesproken voordat men
wist dat elektronen negatief geladen zijn.
15
pulsje
© Noordhoff Uitgevers bv
15/07/13 12:33 PM
Hoofdstuk 3 Elektriciteit
U = ______
12 = 5,0 · 102 en
24 a R = __
I 0,024
0,024
I = ______
G = __
12,0 = 2,0 mS
U
16
pulsje
17
pulsje
18
De lading van een elektron is 1,6 · 10−19 C (Binas
tabel 7). De lading van 1,6 · 1010 elektronen is dus
1,6 · 1010 × 1,6 · 10−19 = 2,6 · 10−9 C.
b I = U · G = 0,05 × 5,0 = 0,25 A en
1 = ______
1 = 20 Ω
R = __
G 0,050
c U = I · R = 1,2 × 4,0 = 4,8 V en
1 = 0,25 S
G = __1 = ___
R 4,0
U = ______
12 · 103 = 96 en
d R = __
125
I
125
I = ______
= 0,010 S
G = __
U 12 · 103
e U = I · R = 12 · 10−3 × 36 · 103 = 4,3 · 102 V en
1
G = __1 = _______
= 2,8 · 10 –5 S
R 36 · 103
19 a Elektronen zijn negatief, dus een overschot.
b De lading van een elektron is 1,6 · 10−19 C (Binas
tabel 7). 3,5 · 10−8 coulomb bevat dus
3,5 · 10−8/1,6 · 10−19 = 2,2 · 1011 elektronen.
20
21
Eerst de lading uitrekenen:
60000 C/s × 0,12 s = 7200 C.
De lading van een elektron is 1,6 · 10−19 C (Binas
tabel 7). 7200 C bevat dus
7200/1,6 · 10−19 = 4,5 · 1022 elektronen.
De lading van een elektron is 1,6 · 10−19 C (Binas tabel 7).
De lading per minuut is dus 250 · 1018 × 1,6 · 10−19 = 40 C.
De stroomsterkte is dan 40 C / 60 s = 0,667 A.
22 a stroomsterkte
b 0,300 A
c Het aantal coulomb is 0,3 × 2 × 60 = 36 C
De lading van een elektron is 1,6 · 10−19 C (Binas
tabel 7). Het aantal elektronen is dan 36/1,6 · 10−19 =
2,25 · 1020 elektronen.
d 0,2 mm2 = 0,002 cm2
Het volume is dus 25 × 0,002 = 0,05 cm3.
De dichtheid van koper is 8,96 g/cm3.
De draad heeft dus een massa van 0,05 × 8,96 =
0,448 = 0,45 g.
e Het aantal vrije elektronen is 0,448/1,1 · 10−22 =
4,1 · 1021.
f In 25 cm draad zitten 4,1 · 1021 elektronen. In
2 minuten worden 2,25 · 1020 elektronen rondgepompt. Deze elektronen zitten in
2,25 · 1020/4,1 · 1021 × 25 = 1,4 cm draad.
De elektronen leggen dus 1,4 cm af in 2 minuten. De
snelheid is 0,014 m /120 s is 1,2 · 10−4 m/s. Nogal
langzaam dus.
25 a Tekenen met de GR of Excel I verticaal en U horizontaal.
I
b De helling is __
, dat is G. Dit is dus de helling.
U
c De functie van de lijn is: y = 1,46 · 10−3 x, dus het
hellingsgetal is 1,46 · 10−3
1 = ________
1
= 6,8 · 102 Ω
R = __
G 1,46 · 10−3
26
27 a A = πr 2 = π · (0,01)2 = 3,14 · 10−4 mm2
b Zoek -zilver op in Binas: 16 · 10 –9 Ωm.
· I 16 · 10−9 × 0,5 · 10−2
R = ___ = ________________
= 0,3 Ω
3,14 · 10−10
A
c De weerstand van de zilverdraadjes is klein: D
10 = 1,7 Ω
28 a R = · __l = 17 · 10−9 × ________
A
0,1 · 10−6
220 · 10−9 × 5,0
220 · 10−9 × 5,0
b _____________ = 4,0 → A = _____________
4,0
A
−7
2
= 2,8 · 10 m
c A = π · r 2 = π × (1,0 · 10−3)2 = 3,14 · 10−6 m2
1 = ______
1 = 20 Ω
R = __
G 0,050
l
· __l = R → 78 · 10−9 × ________
= 20
A
3,14 · 10−6
3,14 · 10−6 × 20
l = _____________
= 8,1 · 102 m
78 · 10−9
3.2 Weerstand
23 a Als G = 0,05 S dan is de stroomsterkte 0,05 A bij 1 V.
b Bij 100 Ω geldt dat bij 5V de stroomsterkte 0,05 A is.
In de grafiek krijg je dan deze lijnen:
29
I in ampère
0,1
a
0,08
0,06
b
0,04
0,02
0
0
© Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_CH03.indd 31
1
2
3
4
U in volt
5
De grootste weerstand heeft een stukje plastic, plastic
wordt immers gebruikt als isolatiemateriaal. De kleinste
weerstand heeft koperdraad, koperdraad wordt
gebruikt als geleider van elektriciteit in bijvoorbeeld een
snoer. Het maakt verschil of je huid droog of vochtig is.
Pulsje
30 a Volgens de wet van Ohm is de stroom recht
U
, dus de weerstand
evenredig met de spanning, I = __
R
waarvan de grafiek een rechte lijn door de
oorsprong is, is een Ohmse weerstand.
b Bij 2,5 V is de stroom door beide weerstanden even
groot, dus de weerstand ook.
Je kunt bij de kromme lijn niet goed spreken over ‘dé’
weerstand.
c Bij een spanning van 1 volt gaat er meer stroom door
de weerstand die wordt aangegeven met de kromme
blauwe lijn, de weerstand is hier dus kleiner.
31
15/07/13 12:33 PM
Hoofdstuk 3 Elektriciteit
d De grafiek loopt steeds minder steil als de spanning
toeneemt. De weerstand neemt dus toe bij grotere
stroom. De temperatuur is dan ook groter. Het is dus
PTC-materiaal.
31 a Bij een iets te grote spanning wordt de stroom
plotseling heel groot. Er treedt dan veel
warmteontwikkeling op waardoor de diode
doorbrandt.
b Er loopt dan zo goed als geen stroom, de weerstand
is dan heel groot.
0,7
U = _____
= 7 · 102 Ω en
c R = __
I 0,001
0,8
U = _____
= 5 · 101 Ω
R = __
I 0,015
d Er loopt dan geen stroom, de weerstand is dus zeer
groot. De grafiek loopt links, op de negatieve V-as
namelijk horizontaal.
32 a We lezen af bij 25 °C: 3000 Ω
5,0
= 0,0017 A.
Daaruit volgt: I = _U_ = _____
R 3000
Door druktechnische reden kan de uitkomst iets
afwijken.
b Als R 2× zo groot is wordt I 2× zo klein.
Bij 9 °C is R = 6000 Ω dus de weerstand moet
25 − 9 = 16 °C afkoelen.
5
= 5000 Ω daaruit volgt dat T = 13 °C
c R = _U_ = _____
I 0,001
(aflezen uit de grafiek)
d Als er door de NTC-weerstand een stroom gaat, dan
wordt elektrische energie omgezet in warmte. Als
de NTC niet voldoende wordt gekoeld, dan stijgt
de temperatuur te sterk, de weerstand daalt, de
stroom neemt toe, nog meer warmte en temperatuurstijging → doorbranden.
35
Nee, als het donker is wordt de weerstand van de
LDR juist groter.
36 a Als de temperatuur hoog wordt, dan wordt de
weerstand laag, dus het is een NTC-weerstand.
b De weerstand R van de glasstaaf is:
230
U = ____
R = __
2,0 = 115 Ω
I
De doorsnede A van de glasstaaf is:
0,45 × 10−2 2
A = π × r2 = π × _________
= 1,59 × 10−5 m2
2
(
De soortelijke weerstand wordt dan:
115 × 1,59 × 10−5
R × A = _____________
= _____
= 0,037 Ωm
5,0 × 10−2
I
3.3 Serie en parallel
37 a De spanning wordt gedeeld, het fietslampje krijgt
6 volt zodat er voor de grote lamp 230 − 6 = 224 V
overblijft.
b De stroom door beide lampen is gelijk, 0,5 A
De weerstand van de grote lamp is dus:
224
2
R = _U_ = ____
0,5 = 448 Ω = 4,5 · 10 Ω
I
38 a U = I · R
U1 = 0,25 × 30 = 7,5 V
U2 = 0,25 × 5 = 1,25 V = 1,3 V
U = U1 + U2 + U3
12 = 7,5 + 1,25 + U3
U3 = 12 − 8,75 = 3,25 V
b R3 = U/I = 3,25/0,25 = 13 Ω
39
De hoofdschakelaar staat in serie met alle apparaten, alle stroom gaat er doorheen vandaar dat je alle
apparaten tegelijkertijd kan uitschakelen.
·I
33 a Er geldt: R = ___ daaruit volgt:
A
0,00030 × 97 · 10−4
R · A = _________________
= ____
= 2,7 · 10−8 Ωm
I
108,0
De stof is aluminium (zie Binas).
b Dan is de doorsnede (evenredig met de dikte in het
kwadraat) meer toegenomen dan met 0,14% dus
·I
R wordt kleiner want R = ____
A
c Voor aluminium geldt = 4,29 · 10−3 K−1.
Invullen in de formule:
R = 0,00030(1 + 4,29 · 10−3 × 60) = 0,00038 Ω
d Het PTC effect geeft een toename van 26%. Dat is
veel groter dan het uitzeteffect van 0,14%.
103 = 9,0 · 10−6 m2
e A = · __l = 180 · 10−9 × ___
20
R
34 a A, er valt meer licht op de LDR, de weerstand
daarvan neemt dus af, er loopt een grotere stroom
en het lampje gaat feller branden.
b De elektronen in de halfgeleider komen door het
licht dat er opvalt in een hogere energietoestand, de
geleidingsband. Er komen daardoor elektronen bij
die de stroom kunnen geleiden. De weerstand
wordt daardoor kleiner.
32
242759_NAT 3E TF HAVO 4 UW_CH03.indd 32
)
apparaten
schakelaar
40 a I = U/R
I1 = 6/30 = 0,20 A
I2 = 6/5 = 1,2 A
I = I1 + I2 + I3
I = 0,20 + 1,2 + 0,25 = 1,7 A
b Gv = I/U = 1,65/6 = 0,28 S
Rv = 1/G = 1/0,275 = 3,6 Ω
41 a Neem een punt tussen twee weerstanden die in serie
staan. In dat punt is de inkomende stroom gelijk aan
de uitgaande stroom, want opgeteld moeten ze nul
zijn volgens de eerste wet van Kirchhof.
© Noordhoff Uitgevers bv
15/07/13 12:33 PM
Hoofdstuk 3 Elektriciteit
b Als je van de bron vertrekt en rond gaat moet de
totale spanning altijd nul zijn ongeacht of je door de
ene tak van de parallelschakeling gaat of door de
andere. De spanning over beide takken moet dus
wel gelijk zijn.
42 a Er wordt mee bedoeld dat het lampje normaal
brandt bij een spanning van 6 volt.
b De stroom door de weerstand en het lampje is
gelijk, de spanning over de weerstand is dan
evenredig met die weerstand.
Als er 6 V staat over een weerstand van 8 Ω, dan
staat er 3 V over een weerstand van 4 Ω.
Dus als de weerstand 4 Ω is, wordt de bronspanning
van 9 V op de juiste manier verdeeld over de
weerstand en het lampje.
43 a Bij 0 °C is de totale weerstand 1100 Ω.
I = U/R
I = 5/1100 = 4,5 · 10−3 A
b U=I·R
U = 100 × 4,5 · 10−3 = 0,45 V
c Bij 80 °C is de weerstand van de NTC 10 Ω.
In serieschakeling geldt dat de spanning evenredig
is met de weerstand.
De verhouding is hier 100 : 10.
De spanning over R is dus 100/110 × 5,0 V.
Dit is 4,5 V.
Je kunt ook eerst de stroomsterkte uitrekenen en
dan de spanning over R, net zoals in de vorige
deelvragen.
44
De weerstand van het gedeelte van de weerstand
van 10 Ω dat parallel staat aan het lampje (R1) is:
7,0
____
9,0 × 10 = 7,78 Ω, het andere gedeelte van de
2,0
weerstand (R2) is ____
9,0 × 10 = 2,22 Ω
De vervangingsgeleidbaarheid van het parallelle
gedeelte is:
1 = 0,212 S → R = 4,72 Ω
1 + __
Gv = ____
v
7,78 12
De totale weerstand is: R = 4,72 + 2,22 = 6,94 Ω
Met verhoudingen berekenen we de spanning die
U1 _____
4,72
het lampje krijgt: ____
9,0 = 6,94 → U1 = 6,1 V
45
Pulsje
6,0
d I = ______________ = 0,33 A
6,0 + 6,0 + 6,0
e De totale weerstand is dan:
6,0
U = _____
Rtot = __
= 12,24 Ω,
I 0,49
De weerstand van de meter is dan:
Rmeter = 12,24 − 12,0 = 0,2 Ω
0,50 − 0,49
f Het percentage is: __________
× 100% = 2%
0,50
Dit is een acceptabele afwijking, dus geen
onnauwkeurige meting.
g De stroom zonder meter is:
6,0
I = ________ = 0,050 A
60 + 60
De stroom met meter is:
6,0
I = ______________ = 0,0499 A
60 + 60 + 0,24
De afwijking wordt dus kleiner.
In verhouding tot de lampjes is de weerstand van de
meter veel kleiner, dus de afwijking ook.
47 a G1 = 1/10 = 0,10 S
G2 = 1/15 = 0,067 S
Gv = 0,10 + 0,067 = 0,167 S
Rv = 1/0,167 = 6 Ω
b Rv = 6 + 30 = 36 Ω
c De totale stroomsterkte is
I = U/R = 9/36 = 0,25 A
De spanning over R3 is dus U = I · R = 0,25 × 30 = 7,5 V.
d De spanning over R1 is 9,0 − 7,5 = 1,5 V.
De stroomsterkte is dus I = U/R = 1,5/10 = 0,15 A.
48 a UR1 = I · R1 = 0,5 × 14 = 7 V
b De spanning over R3 en R4 is 12 − 7 = 5 V, dus:
5
U = ___
IR3 = __
= 0,13 A
R3 40
5
U = ___
IR4 = __
= 0,17 A
R4 30
c De stroomsterkte door R2 is 0,5 − 0,13 − 0,17 = 0,2 A,
dus:
5
U = ___
= 25 Ω
R2 = __
IR2 0,2
___
1
1
1 ___
d Gv = ___
25 + 40 + 30 = 0,0983 → Rv = 10 Ω
òf
5
U = ___
= 10 Ω
Rv = __
I 0,5
49 a
46 a
9,0 V
6,0 V
6,0 Ω
6V
0,5 A
6,0 Ω
6V
0,05 A
A
b De meter mag overal in de schakeling in serie worden
opgenomen omdat de stroom I overal gelijk is.
6,0
U = _________
= 0,50 A
c I = __
R 6,0 + 6,0
© Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_CH03.indd 33
b De stroomsterkte is dan 0,05 A
c De stroomsterkte is even groot, ook 0,05 A
6 = 12 Ω
U = ___
d R = __
I 0,5
e U = I · R = 0,05 × 12 = 0,6 V
f Ubron = 6 + 0,6 = 6,6 V
33
15/07/13 12:33 PM
Hoofdstuk 3 Elektriciteit
d Invullen levert:
A: −0,25 + I1 + 0,15 = 0 → I1 = 0,10 A
C: −0,15 − I3 + 0,05 = 0 → I3 = −0,10 A Kennelijk loopt
de stroom door R3 juist naar boven.
D: −I2 − 0,05 + 0,25 = 0 → I2 = 0,20 A
B: −0,10 + −0,10 + 0,20 = 0 → klopt
e R1 = U/I = 1,0/0,10 = 10 Ω
R2 = U/I = 5,0/0,20 = 25 Ω
R3 = U/I = 1,0/0,10 = 10 Ω
R4 = U/I = 2,0/0,15 = 13 Ω
R5 = U/I = 4,0/0,05 = 80 Ω
g Het voorlampje is kouder dan wanneer het goed
brandt en heeft dus een kleinere weerstand (PTC)
dan berekend. Het voorlampje krijgt dus een
kleinere spanning dan berekend en ook de bronspanning is kleiner.
h Het achterlampje brandt niet meer omdat de
stroomkring is onderbroken.
50 a
12 Ω
15 Ω
20 Ω
b De grootste stroom loopt door de kleinste weerstand, dat is de weerstand van 12 Ω
c Gv = G2 + G2 + G3
Gv = 1/12 + 1/15 + 1/20 = 0,20 S
d De stroomsterkte was 1,8 A (ga dat zelf na met de
bronspanning en de vervangingsgeleidbaarheid).
Door de nieuwe weerstand R4 loopt dus 0,2 A.
9,0
U = ____
dus R4 = __
= 45 Ω
I 0,2
of: De totale vervangingsgeleidbaarheid is nu:
2,0
I = ____
Gv = __
= 0,222 S
U 9,0
54 a De spanningsmeter hoort de helft van 6,0 V aan te
geven. Dat is 3,0 V
1 = 0,333 → R = 3,0 Ω
1 + ____
b Gv = ____
v
6,0 6,0
c Deze weerstand is 1⁄3 gedeelte van de totale
weerstand. De spanning is dus ook 1⁄3 gedeelte.
1
U = __
3 × 6,0 = 2,0 V in plaats van 3,0 V
d De weerstand van de spanningsmeter is vergeleken
met de weerstand van het lampje oneindig groot.
De spanningsmeter meet dus 3,0 V
In werkelijkheid is het iets minder maar dat valt
binnen de afleesnauwkeurigheid.
55 a en c
10 Ω
12 V
60 Ω
Gv = 0,222 = 0,200 + G4 → G4 = 0,022 → R4 = 45 Ω
51 a
20 Ω
6V
A
10 Ω
V
b De spanningsmeter wijst 2,67 V aan.
De vervangingsweerstand van de parallel
geschakelde takken is:
1
1 + _______
→ Rv = 20 Ω
Gv = ___
60 20 + 10
LED
b De spanning is dan 2,0 volt (zie grafiek)
52
De totale weerstand in de keten is:
Rtot = 20 + 10 = 30 Ω
De stroom in de keten is:
12 = 0,40 A
I = _U_ = ___
R 30
Pulsje
53 a −Ub + U1 + U2 = 0
−Ub + U4 + U5 = 0
−Ub + U1 + U3 + U5 = 0 (neem aan dat door R3 de
stroom naar beneden loopt.)
−Ub + U4 − U3 + U2 = 0 (U3 werkt dan tegen)
b Invullen levert:
−6 + 1 + U2 = 0 → U2 = 5,0 V
−6 + U4 + 4 = 0 → U4 = 2,0 V
−6 + 1 + U3 + 4 = 0 → U3 = 1,0 V
−6 + U4 − U3 + U2 = 0 →
−6 + 2 − 1 + U2 = 0 → U2 = 5,0 V
c A: −It + I1 + I4 = 0
B: −I1 + I3 + I2 = 0
C: −I4 − I3 + I5 = 0
D: −I2 − I5 + It = 0
34
242759_NAT 3E TF HAVO 4 UW_CH03.indd 34
De spanning over de parallelle weerstanden is:
U = I · R = 0,40 × 20 = 8,0 V
De stroom door R1 en R2 is:
8,0
= 0,267 A
I = _U_ = ___
R 30
De spanning over R2 is:
U = I · R = 0,267 × 10 = 2,67 V
d I = 0,267 A, voor berekening zie vraag b.
56
Pulsje
57 a Zonder spanningsmeter is U = 20,00 V.
Met spanningsmeter is het anders, want de vervangingsweerstand van de 1000 Ω-weerstand en de
weerstand van de spanningsmeter is:
© Noordhoff Uitgevers bv
15/07/13 12:33 PM
Hoofdstuk 3 Elektriciteit
______
1
1
= _____
1000 + 2 · 106 → Rv = 999,5 Ω
40,00
U = ______
= 0,020005
I = __
R 1999,5
Umeter = I · R = 0,020005 × 999,5 = 19,995 V
Ja. Het scheelt 0,005 V. Er is met een nauwkeurigheid van 0,01 V te meten.
b Nee: Als je de weerstanden 10× zo groot neemt
(10 000 Ω), worden alle afwijkingen ook 10× zo
groot. Reken maar na.
Er moet bij gezet worden wat de afwijking is
afhankelijk van de te meten weerstanden.
__
1
Rv
58 a De gebruikte weerstand moet klein zijn omdat:
1 De stroom moet er gemakkelijk doorheen kunnen.
2 De spanning over het interface mag niet groter
worden dan 10 V. Die spanning is recht evenredig
met de weerstand bij een bepaalde stroomsterkte.
5,0
U = ___
= 2,5 A
b I = __
R 2,0
c De spanning moet worden gedeeld door de weerstandswaarde, hier dus door 2,0.
59 a
R
naar
interface
(max. 10 V)
b Als de te meten spanning 400 V is, moet over
weerstand R 10 V staan en over de grote weerstand
390 V.
De stroom is hetzelfde dus R is 39× kleiner dan de
grote weerstand: R = 100 : 39 = 2,56 = 2,6 kΩ.
60 a Bij 20 °C is de weerstand ongeveer 0,23 kΩ
De totale weerstand is 10,0 kΩ + 0,23 kΩ = 10,2 kΩ
1,5
I = _________3 = 1,47 · 10−4 A
10,23 . 10
UNTC = I · R = 1,47 · 10−4 × 0,23 · 103 = 0,034 V
Omdat de grafiek niet nauwkeurig af te lezen is,
mag je uitkomst ca. 0,003 V afwijken.
b Hij heeft de spanningsmeter aangesloten over de
weerstand van 10 kΩ
Immers, als T stijgt daalt de weerstand van de NTC,
er komt dan minder spanning over de NTCweerstand te staan en meer over de andere weerstand.
3.4 Elektrische energie
275
E = ___
= 55 W
61 a Het vermogen is: P = __
t 5,0
45 · 106
E = ____________
b P = __
= 1,98 · 103 W = 2,0 kW
t 6,3 × 60 × 60
45 · 106
c E = _______6 = 12,5 kWh
3,6 · 10
of: E = 1,98 kW × 6,3 h = 12,5 kWh
© Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_CH03.indd 35
63 a De stroomsterkte I = 0,13 A en het vermogen
P = U · I = 1,6 W.
De spanning U volgt uit:
1,6
P = ____
= 12,3 = 12 V.
U = __
I 0,13
12,3
U = ____
b R = __
= 95 Ω
I 0,13
64
P=U·I
U=I·R
P = I · R · I = I2 · R
0,0095 = I2 × 150
I2 = 0,0095/150 = 0,000063
I = 0,008 A = 8,0 mA
65 a 375 omwentelingen ≅ 1 kWh = 3,6 · 106 J
3,6 · 106
3
1 omwenteling: ≅ _______
375 = 9,60 · 10 J
b Je zet de waterkoker aan en meet de tijd gedurende
een aantal omwentelingen van de kWh-meter. Je
rekent de toegevoerde energie uit in joule. Daarna
deel je de toegevoerde energie (in J) door de tijd
(in s) en je krijgt dan het vermogen in J/s = W.
100 kΩ
te meten
spanning
(max. 400 V)
62 a 1 kilowattuur = 1 kWh = 1000 W · 3600 s =
3,6 · 106 Ws = 3,6 · 106 J.
b De joule is voor het dagelijkse leven een te kleine
eenheid.
66 a P = U · I = 1,5 × 0,060 = 0,090 W
1,5
U = ______
= 25 Ω
b R = __
I 0,060
c In 4 uur is de geleverde energie:
E = U · I · t = 1,5 × 0,60 × 4 × 3600 = 1,3 · 103 J
Tussen 4 en 5 uur daalt de spanning, dus ook de
stroom. Gemiddeld U = 0,75 V en I = 0,03 A
dus: E = 0,75 × 0,03 × 1 × 3600 = 81 J
Bij lagere temperatuur neemt de weerstand van de
gloeidraad af dus het zal iets meer zijn dan 81 J.
Totaal: E = 1,4 · 103 J
67 a De elektrische energie wordt omgezet in warmte.
b R = 3000 Ω hieruit volgt:
5
U = _____
= 1,7 · 10−3 A
I = __
R 3000
P = U · I = 5 × 1,7 · 10−3 = 8,3 · 10−3 W
Dus per seconde wordt dat: 8,3 · 10−3 J. Door druktechnische reden kan de uitkomst iets afwijken.
c De temperatuur neemt dan toe, de weerstand
neemt dus af dus de stroom neemt toe en het
vermogen neemt toe.
68 a
spanning in V
stroom in mA
vermogen in mW
0
0
0
1,5
2,1
3,2
3
4,5
13,5
4,5
6,5
29,3
6
8,9
53,4
7,5
10,9
81,8
35
15/07/13 12:33 PM
Hoofdstuk 3 Elektriciteit
b
80
U in V
vermogen in mW
c Bij ongeveer 28 Ω.
d
35,0
P-I-grafiek
90
70
60
15,0
40
30
10,0
20
5,0
10
0
0
2
4
6
__
30,9
0,00
0,0
100
28,8
0,29
8,4
50
27,0
0,54
14,6
25
22,5
0,90
20,3
3
3,1
1,03
3,2
0
0,0
1,10
0,0
25,0
20,0
0,80
1,00
1,20
P in mW
700
600
300
200
100
0
20 30 40 50 60 70 80 90
T in °C
g Als je de lijn doortrekt, kom je uit bij 300 W.
h Bij 75 °C is P 458 W en bij 25 °C 740 W. Dat is 282 W
kleiner, en dat is 38% kleiner. Dus dit is in
overeenstemming met de hypothese.
i P = U · I. Het vermogen is maximaal als I maximaal is
en tegelijkertijd U maximaal. Je moet dus kijken bij
de waarden waar de grafiek een knik maakt. Dat is
dus bij 4 A en 29 V.
Pmax = 4 × 29 = 116 W = 1,2 · 102 W
j De oppervlakte van het paneel is 60 × 0,1562 =
1,46 m2. Het toegevoerde vermogen is dus
600 × 1,46 = 876 W
Het rendement is dus 116/876 = 13%.
P
in W
open circuit
0,60
400
69 a
stroomsterkte
in A
0,40
500
_____
Je zou ook de grafiek kunnen gebruiken. De grafiek
loopt niet door tot aan het maximale vermogen
(0,25 W). Truc: wanneer je de stroom afleest die hoort
bij 1/4 van het maximaal vermogen, dan is de stroom
1
/2 van het maximum. Bij 0,0625 W hoort 9,5 mA, dus
er mag maximaal 19 mA doorheen.
f De spanning U wordt:
U = I · R = 0,019 × 688 = 13,1 V
Dit is de maximale spanning die je erop mag zetten.
Je neemt hierbij aan dat de weerstand gelijk blijft, dat
wil zeggen dat hij niet verandert als gevolg van
temperatuurverschillen.
spanning
in V
0,20
e Pmax = 21 W
De oppervlakte van het paneel is 0,50 × 0,75 =
0,375 m2.
Toegevoerd vermogen is dus 300 × 0,375 = 113 W.
Rendement is dus 21/113 = 19%.
f
800
0,25
P = ____
De stroom wordt dan: I = __
= 0,019 A
R
688
weerstand
in Ω
0
I in mA
8
10
12
stroom in mA
c Bij 5 mA is het vermogen 17 mW en bij 10 mA is het
vermogen 69 mW.
d Als de stroom met een factor 2 toeneemt, dan
neemt het vermogen met een factor 4 toe.
e Het maximale vermogen is dan 250 mW, dat is 0,25 W.
De stroom berekenen we als volgt:
Het vermogen P is: P = I2 · R
7,5
U = _______
= 688 Ω
De weerstand R is: R = __
I 0,0109
P in W
25,0
20,0
50
0
b
30,0
70
3.5 Elektriciteit veilig in huis
Opdelen in groepen heeft als voordeel dat als er een
groep uitvalt de andere groepen nog functioneren.
De groepen zijn apart uit te schakelen en dat is
handig bij het klussen of het opsporen van
storingen.
15,0
10,0
5,0
0
0
20
40
60
80
100 120
weerstand in Ω
36
242759_NAT 3E TF HAVO 4 UW_CH03.indd 36
© Noordhoff Uitgevers bv
15/07/13 12:33 PM
Hoofdstuk 3 Elektriciteit
71 a De zonnepanelen sluit je aan voorbij de meter.
b Als hij op een goed isolerende ondergrond staat,
of als hij het draadje vasthoudt vlakbij de ‘nul’aansluiting, zal het wel meevallen.
c Het ijzerdraadje krijgt een hoge temperatuur
doordat er een grote stroom doorheen gaat. De zeer
jonge onderzoeker brandt waarschijnlijk zijn
vingers.
groep 1
groep 2
Toepassing
Opgave 1 Het zonnewagentje
1
Als er geen stroomkring is, loopt er ook geen
stroom. De stroomsterkte is dan nul.
hoofdschakelaar
kWh-meter
fasedraad (230 V)
nuldraad
schakeldraad
2
U
R = __
I
RB = 0,06/1,0 · 10−3 = 60 Ω
RC = 0,91/0,25 · 10−3 = 3,6 · 103 Ω
3
Nee, want de weerstand is niet constant.
4
P=U·I
PB = 0,06 × 1,0 · 10−3 = 6 · 10−5 W
PC = 0,91 × 0,25 · 10−3 = 2,3 · 10−4 W
5
Rendement in B is nul, want de wielen draaien niet.
De bewegingsenergie is hier de nuttige energie.
6
s = vgem · t → vgem = 0.3/1 = 0,3 m/s
Dus veind = 0,6 m/s
a = Δv/Δt = 0,6/1 = 0,6 m/s2
7
De snelheid is constant van 1,5 tot 2,0 s.
vgem = (1,15 − 0,67)/0,5 = 1,9 m/s
P=F·v
2,3 · 10−4 = F × 1,9
F = 1,2 · 10−4 N
A
b De spanning is iets hoger dan 230 V. Hierdoor
vormen de zonnepanelen de bron, en loopt er ook
nog stroom door de kWh-meter naar het net.
72 a Aardlekschakelaar; er ontstaat geen kortsluiting dus
de zekering reageert niet, de aardlekschakelaar
reageert wel want er vloeit stroom via het kind weg
naar de aarde. NIET proberen: gevaarlijk!
b Zekering; de stroom is te groot zodat de zekering
reageert. Er vloeit geen stroom weg dus de aardlekschakelaar reageert niet.
c Zekering; er ontstaat kortsluiting. De zekering
reageert, de aardlekschakelaar reageert niet.
d Beide; zowel de zekering als de aardlekschakelaar
kunnen reageren. Er loopt een te grote stroom én er
loopt stroom weg via de aarde. De aardlekschakelaar
reageert het snelst.
73
Opgave 2 Bodemonderzoek
8/11
Doordat er langere tijd een te grote stroom door de
smeltzekering liep, is de temperatuur in die tijd sterk
gestegen. Dus er was sprake van overbelasting.
A
V
74 a Droge huid is een slechte geleider. Door de huid met
een geleidende pasta in te smeren wordt hij beter
geleidend.
b Bij een groot huidoppervlak is de huidweerstand
klein en de stroom kan gemakkelijk door de huid het
hart bereiken. Als alle stroom door een klein stukje
huid zou moeten is de weerstand groot en zou de
huid ook plaatselijk te heet kunnen worden.
75 a Als de weerstand van je lichaam 0 Ω zou zijn dan is
de stroom maximaal. Dat is dan:
230 V
U = __________
= 0,00036 A = 0,36 mA
I = __
R 0,64 · 106 Ω
b 0,02 = I2 · t → 0,02 = 0,000362 · t
→ t = 1,5 · 105 s = 43 uur
76 a De zekering zal reageren want er ontstaat kortsluiting. NIET proberen: gevaarlijk!
© Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_CH03.indd 37
–
+
9
l 1
R = __ = __
A G
A , = __1 en l = d
G = __
l
A ⇒ = ___
Gd
⇒ G = ___
A
d
37
15/07/13 12:33 PM
Hoofdstuk 3 Elektriciteit
10
2,8 · 10−3
I = ________
−4
G = __
5,0 = 5,6 · 10 S
U
d = 0,01 m, A = 0,0202 = 4,0 · 10−4 m2
Opgave 4 Waarschuwingsled
19
5,6 · 10−4 × 0,01
Gd = _____________
= ___
= 0,014 Ω−1 m−1
4,0 · 10−4
A
De totale lading van de chloride-ionen is
2,4 · 1019 × 1,6 · 10−19 = 3,84 C De stroomsterkte,
die door de chloride-ionen verzorgd wordt is 0,90 ×
2,8 = 2,52 mA
2,52 · 10−3 C komt in 1 sec aan bij de elektrode.
Dat is 2,52 · 10−3/3,84 = 6,56 · 10−4 van de totale
lading. De totale lading schuift dus ook dit deel van
1,0 cm in de richting van de pluspool. Dat is dus
6,56 · 10−6 m in 1 seconde.
De snelheid is 6,6 · 10−6 m/s.
Opgave 3 Bolbliksem
13
<wikipedia>
- Sommige deskundigen denken dat het gewoon een
blikseminslag is, waarvan het beeld secondenlang
op het netvlies blijft staan.
- Er zijn ook mensen die beweren dat ze het door het
glas via een spiegel hebben waargenomen, zodat
het niet direct op het netvlies geschreven kan
worden.
- Een recente verklaring van onderzoekers uit
Nieuw-Zeeland gaat ook uit van een blikseminslag.
Als de hoeveelheid koolstof in de grond bij het
inslagpunt 1 à 2 keer groter is dan de hoeveelheid
siliciumoxide, ontstaat bij een temperatuur boven
3000 graden silicium of verbindingen daarvan. Heel
kleine deeltjes hiervan vormen fijne dradennetwerken in de vorm van pluizige bollen. De energie die de
bol doet gloeien is het gevolg van oxidatie.
- Een andere verklaring is het aansteken van sporen
van aardgas of moerasgas door een zware bliksemontlading.
14
20
Bij een lage temperatuur is de weerstand van de
NTC groot. Hierdoor is de spanning over de NTC
groot en de spanning over de LED dus klein. Als de
spanning over de LED kleiner is dan 1,5 V brandt de
LED niet. (Bij een hogere temperatuur brandt de LED
dus wel)
21
Uitkomst: R = 3,0 · 102 Ω
Aflezen in figuur 6: bij 20°C geldt RNTC = 5,9 · 102 Ω.
Aflezen in figuur 7: bij 1,0 mA geldt ULED = 1,5 V.
Daaruit volgt: UNTC = 5,0 − 1,5 = 3,5 V.
Er geldt
UNTC ____
3,5
= 5,93 · 10−3
=
INTC = ____
RNTC 590
ILED = 1,0 mA zodat IR = 5,93 · 10−3 − 1,0 · 10−3 =
4,93 · 10−3 A.
Voor R van de variabele weerstand geldt nu:
U
1,5
= 3,0 · 102 Ω
R = ___R = _________
IR 4,93 · 10 –3
Opgave 5 Een temperatuursensor maken
22
5
u sensor in V
12
3
2
R = U/I = 5000/60 = 83 Ω
1
15
E = P · t = U · I · t = 5000 × 60 × 0,1 = 3 · 104 J
0
16
Water bestaat uit ongeladen moleculen die de
stroom niet geleiden.
(Bij scheikunde leer je dat ook zuiver water een
geringe hoeveelheid H+ en OH− ionen bevat, die
bijdragen aan een geringe stroomgeleiding.)
17
Je weet niet waar en wanneer de bliksem inslaat.
18
De geluidssnelheid is bij 25 °C gelijk aan 343 m/s.
In 8 s legt het geluid dus 8 × 343 = 2,7 · 103 m af.
Het licht gaat zo snelheid dat je de tijd daarvoor
mag verwaarlozen:
t = 2,7 · 103/3 · 108 = 9 · 10−5 s.
Deze tijd is verwaarloosbaar klein vergeleken met
de 8 s.
38
242759_NAT 3E TF HAVO 4 UW_CH03.indd 38
A
C
4
B
0
t in °C
23
De spanning over de NTC en de spanning over de
weerstand zijn samen gelijk aan 5,0 V. Als de
temperatuur hoger wordt, daalt de weerstand van
de NTC. Hierdoor daalt ook de spanning over de
NTC. Dus neemt de spanning over de weerstand (dit
is de sensorspanning) toe.
24
Voor het vermogen van de NTC geldt:
P = I2 · RNTC
Invullen levert: INTC = 0,953 · 10−3 A
Voor de spanning over de NTC geldt dan:
UNTC = INTC · RNTC = 0,953 · 10−3 × 2,2 · 103 = 2,1 V.
Voor de grootte van de weerstand geldt dan:
5,0 − 2,1
= 3,0 · 103 Ω
R = _U_ = __________
I 0,953 · 10−3
© Noordhoff Uitgevers bv
15/07/13 6:03 PM
Hoofdstuk 3 Elektriciteit
Opgave 6 Valentijnshart
25
C
3 a
D
koper
= 17 · 10 –9 Ωm
·I
0,10 × 3,0 · 10−6
R · A = _____________
R = ___ → I = ____
= 18 m
A
17 · 19−9
b A = πr 2 → als r 2 × zo groot is dan is A dus 4 × zo groot.
c R is omgekeerd evenredig met de doorsnede, dus R
is dan 4 × zo klein.
+
A
–
B
26
4 a
R2
R1
5,0 Ω
A
6,0 V
3,0 W
R
V
stroommeter
27
spanningsmeter
De vijf parallel geschakelde LED’s aan de linkerkant
staan in serie met de grote LED en de vier parallel
geschakelde LED’s aan de rechterkant. Hieruit volgt
dat UL + UR = 4,0 V.
De vervangingsweerstand van de vijf LED’s aan de
linkerkant is kleiner dan de vervangingsweerstand
van de vier LED’s aan de rechterkant.
Daaruit volgt dat UL < UR, dus dat UL < 2,0 V.
Proefwerkopgaven
1 a De aardlekschakelaar reageert. Er vloeit een stroom
via het kind naar de aarde, de aardlekschakelaar
detecteert dat en sluit de stroom af.
b Dit gaatje is verbonden met de nuldraad. Deze is blauw.
2 a
A
V
b Nee, de stroom is niet recht evenredig met de spanning
want de grafiek is geen rechte lijn door de oorsprong.
c Volgens de tweede wet van Kirchhoff is de totale
spanning in een kring nul. Als twee
spanningsbronnen in serie zijn geschakeld, dan
moet je beide spanningen dus bij elkaar optellen.
d Aflezen uit de grafiek bij 3,0 V: I = 0,56 A
e Er geldt: aantal uren × stroomsterkte = 0,650
aantal uren × 0,56 = 0,650
conclusie: aantal uren = 0,650 : 0,56 = 1,16 uur
(1 uur en 10 minuten)
© Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_CH03.indd 39
b De weerstand moet heel groot zijn ten opzichte van
de gebruikte weerstanden, want er moet zo weinig
mogelijk stroom vloeien door de voltmeter.
c De spanning over R1 is hetzelfde als over het lampje,
dus:
6,0
U = _____
= 20 Ω
R1 = __
I 0,30
d P = U · I, dus
3,0
0,50
I = _____
P = ____
= 0,50 A → G = __
= 0,083 S
I = __
U 6,0
U
6
e De stroom door R2 is 0,30 + 0,50 = 0,80 A
De spanning over R2 is dus:
U = I · R = 0,80 × 5,0 = 4,0 V
Het vermogen is dus:
P = U · I = 4,0 × 0,80 = 3,2 W
__
1
1
1 = G = G + G = ___
f __
v
1
2
20 + 12 → Rv = 7,5 Ω
Rv
Rtotaal = 7,5 + R2 = 7,5 + 5,0 = 12,5 Ω
òf
Utotaal _________
4, 0 + 6,0 _____
10,0
=
= 12,5 Ω
=
Rtotaal = _____
Itotaal
0,80
0,80
g De totale weerstand wordt groter.
De stroom door R2 wordt kleiner.
De spanning over R2 wordt kleiner want U is evenredig met I bij constante weerstand.
De spanning U over R1 wordt dus groter.
Er gaat dus meer stroom door R1 lopen. De stroommeter geeft meer aan.
5 a Voor een temperatuurstijging van 88 graden
(100 − 12) is nodig: E = 4,2 kJ × 88 = 3,7 · 105 J
3,7 · 105
E → t = __
E = ____________
b P = __
= 335 s = 5,6 min
P 1,2 · 103 × 0,92
t
335
c 335 s = _____ = 0,093h
3600
E = P · t = 1,2 × 0,093 = 0,11 kWh
Dat kost: 0,11 × 0,23 = € 0,03
39
15/07/13 12:33 PM
Hoofdstuk 4 Kracht en beweging
Hoofdstuk 4
Kracht en beweging
1
2
Introductie
Voorbeelden ter ondersteuning:
Een bowlingbal valt sneller dan een sneeuwvlok.
Een knikker valt sneller in lucht dan in stroop.
Tegenvoorbeeld:
Een zware en een lichte bowlingbal vallen vrijwel
even snel.
3
Laat je antwoord door je docent controleren.
Belangrijke fouten in zijn logica zijn:
- dat de lucht de bewegende kogel aandrijft,
- dat de valbeweging pas begint als de kogel tot
stilstand is gekomen.
4
Dankzij een ontmoeting van de astronoom met
Newton is er een gedeelte over planeetbanen in
Principia gekomen. Principia (geschreven door
Newton) is door Halley geëditeerd en gepubliceerd.
5
Door de baan van deze komeet te voorspellen kon
Newton zijn theorie over zwaartekracht bewijzen
4.1 Weerstand en beweging
1 a Luchtweerstand
b Rolweerstand
2 a Luchtweerstand
b De luchtweerstand hangt onder andere af van de
snelheid, het frontale oppervlak en de vorm.
3 a Volgens Aristoteles zijn alleen gedwongen
bewegeningen of natuurlijke bewegingen mogelijk.
Zonder aandrijvende kracht is er geen gedwongen
beweging, je fiets staat dus stil. Er is alleen nog een
natuurlijk beweging mogelijk (vallen).
b Volgens Newton sta je stil of je beweegt met
constante snelheid in een rechte lijn.
4
lichaam versnelt minder dan de scooter en je valt er
af. Dit kun je voorkomen door je goed vast te
houden aan de bestuurder.
b Je lichaam probeert dezelfde snelheid te houden
en je schuift tegen de bestuurder aan. Dankzij de
kracht die de bestuurder met zijn rug uitoefent
wordt je lichaam dan even hard afgeremd als de
scooter.
Vacuüm heeft dichtheid nul. Als de snelheid
omgekeerd evenredig is met de dichtheid, dan
vallen alle voorwerpen in vacuüm met de snelheid
__1
0 = ∞.
Een beweging stopt niet echt vanzelf. De weerstand
met de lucht, de weg, enzovoorts, zorgt ervoor dat
de beweging stopt. Omdat er altijd wel weersstandskrachten zijn lijkt het vanzelfsprekend dat
elke beweging stopt als je geen kracht meer
uitoefent.
5 a Door je traagheid blijft je lichaam achter bij de
scooter. De kracht die nodig is om jou te versnellen
is groter dan de schuifweerstand van je achterste. Je
40
242759_NAT 3E TF HAVO 4 UW_CH04.indd 40
6
Pulsje
7
Pulsje
8 a Dan kost het minder kracht en dus minder energie
om je snelheid te behouden.
b Je banden zo hard mogelijk oppompen.
c Je kunt dan wegglijden en vallen, en niet goed
remmen.
d Opgevroren wegdek, bladeren, modder, olie, gladde
banden.
9 a De luchtweerstand is nihil, er is geen schuifweerstand en de rolweerstand is klein. Er is dus weinig
kracht nodig om een constante snelheid te houden.
b Als de snelheid moet veranderen in grootte of
richting, dus:
- als je door de bocht gaat,
- als je wilt versnellen,
- als je wilt afremmen.
En natuurlijk ook als er een wiel aanloopt
(schuifweerstand).
c Bij een volle kar, met de grootste massa
10
Doordat de schaatsen het ijs niet meer raken
ondervindt de schaatser geen zijwaartse schuifweerstand meer. De netto kracht is (vrijwel) nul en
de schaatser beweegt met (vrijwel) constante
snelheid in een rechte lijn.
11
Door de traagheid heeft het vloeibare binnenste van
het rauwe ei nog snelheid. Danzij deze snelheid
komt het rauwe ei weer op gang.
Bij het gekookte ei wordt het binnenste ook direct
stilgezet, je voelt ook dat dit meer kracht kost.
12
Als je langzaam trekt breekt het bovenste touwtje,
omdat daar je spierkracht plus de zwaartekracht op
werkt.
Als je een snelle ruk aan het touwtje geeft is de
kracht in het onderste touwtje veel groter. Voor het
bovenste touwtje duurt dat even omdat eerst de
massa in beweging moet komen. Maar dan is het
onderste touwtje al geknapt.
© Noordhoff Uitgevers bv
15/07/13 12:33 PM
Hoofdstuk 4 Kracht en beweging
Er is geen weerstand, dus de aarde zou verder
bewegen in een rechte lijn met constante snelheid,
zoals in opdracht 7.
21 a
14 a Op de maan is de zwaartekracht kleiner dan op
aarde. De spierkracht van de astronaut is daarentegen even groot gebleven. Hij tilt dus gemakkelijker
een steen met een even grote massa op de maan op
dan dat hij dat op aarde doet.
b Bij het weggooien (in beweging brengen) speelt
alleen de traagheid van de steen een rol. De traagheid van de steen is op de maan even groot als op
aarde. Als hij de steen dus makkelijker optilt,
verwacht hij hem ook makkelijker te kunnen
weggooien, maar dat lukt niet. Zijn ruimtepak
hindert hem ook nog eens extra.
15 a De normaalkracht
b Dan voel je je lichter.
c De lift vertraagt maar jij gaat door je traagheid nog
even door. Daardoor is er minder kracht tussen je
voeten en de vloer: dat voelt lichter.
16 a De weerstand met het water zorgt er voor dat het
onderstel achterblijft.
b De weerstand tussen de boot en het onderstel is
veel kleiner. De boot verliest dus niet veel vaart en
schiet door.
c De traagheid van de boot zorgt ervoor, dat deze met
dezelfde vaart doorschiet over het water. Pas als hij
het water raakt wordt hij afgeremd. Als de stroomlijn van de boot goed is remt hij niet zo hard af en
kan hij de bel bereiken.
d Als je zo’n onderstel gebruikt kun je ervoor zorgen
dat hij erg hard van de helling afglijdt, dat de boot
niet opzij kantelt en horizontaal op het water komt.
Je er ook voor zorgen dat je boot een eindje boven
het water vooruit schiet, dus nog niet afremt op het
water zelf.
4.2 Kracht en versnellling
17 a recht
b omgekeerd
c recht
18
C
19
∆v
a = ___
∆t
Fnetto
a = ____
m
© Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_CH04.indd 41
20
10
0
0
1
2
3
4
5
6
t in s
2,78 m/s
___
∆v ________
2
b a = ∆t = 1,25 = 2,2 m/s
Fnetto = m · a = 62 × 2,2 = 1,4 · 102 N
De netto kracht is ook de extra kracht, want de kracht
die er al was, was nodig om de snelheid constant te
houden.
22 a Dat hoeft niet. Als de versnelling maar kort duurt
dan is de snelheid niet zo groot.
b Nee. De sprinkhaan heeft een kleine massa (traagheid). De kracht hoeft dan niet groot te zijn.
23
De kracht die je uit kunt oefenen op je pedalen
verandert niet. Die is als je fietst met iemand
achterop even groot als zonder die persoon.
Toen je alleen fietste, gold: a = 3,0 m/s2; m = 70 kg
Daaruit volgt:
Fnetto = m · a = 70 × 3,0 = 2,1 · 102 N
Met je vriend achterop wordt het:
mtotaal = 55 kg + 15 kg + 70 kg = 140 kg
Fnetto = 210 N
Fnetto ___
210
2
Dus: a = ____
m = 140 = 1,5 m/s
Een snellere en ook juiste redenering is: De totale
massa wordt twee keer zo groot bij dezelfde kracht.
De versnelling wordt dus twee keer zo klein.
F
netto
24 a Je gebruikt a = ____
m . De massa moet in kg.
Dus wordt het m = 250 g = 0,25 kg
10
2
→ a = ___
0,25 = 40 m/s
___
∆v
b a = ∆t Dus ∆v = a · ∆t. Hieruit volgt dan: ∆v = 40 ×
0,20 = 8 m/s. Omdat je begint met een snelheid van
0 m/s, is dat ook de eindsnelheid.
c 5,0 N, de versnelling wordt twee keer zo klein bij
dezelfde massa. Dan is de benodigde kracht ook
twee keer zo klein.
25
a = (∑iFi )/m
20 a De Opel doet het kortst over optrekken naar
100 km/h, namelijk 6,5 s.
b De Opel heeft een groter motorvermogen dan de
Skoda.
91
= 1,06 × zo klein, maar de massa
c Het vermogen is __
86
___
1122
is wel 882 = 1,27 × zo klein. De verhouding tussen het
vermogen en de massa is dus gunstiger.
d De verhouding tussen het vermogen en de massa is
ongeveer gelijk.
30
v in km/h
13
26
0,50
0,50 g = _____
1000 = 0,00050 kg
∆v = _____
12 =
De versnelling van het propje is a = ___
∆t 0,015
2
800 m/s
Hiervoor is een kracht nodig van
Fnetto = m · a = 0,00050 × 800 = 0,40 N
40
vgem = ___
3,0 = 13,3 m/s
als de beginsnelheid nul is, is de eindsnelheid dus
2 × 13,3 = 26,7 m/s, dus ∆v = 26,7 m/s
26,7
∆v ___
= 3,0 = 8,89 m/s2
a = ___
∆t
Fnetto = m · a = 60 × 8,89 = 5,3 · 102 N
41
15/07/13 12:33 PM
Hoofdstuk 4 Kracht en beweging
27
Laat je werk controleren door je docent.
28 a 180 N is de stuwkracht. Dit is niet de netto kracht: er
is altijd sprake van weerstand. De netto kracht valt
af te leiden uit de versnelling:
Fnetto = m · a = 125 × 1,2 = 1,5 · 102 N
b 30 N, omdat er maar 150 N van de
180 N stuwkracht over is moet er een tegenwerkende kracht zijn van 30 N. Dat is de weerstand.
Of formeler: Fnetto = Fstuw + Fweerstand zodat
Fweerstand = Fnetto − Fstuw = 150 − 180 = −30 N
Het –teken betekent dat de weerstand tegenwerkt.
c Als de snelheid groter wordt neemt de luchtweerstand ook toe, de rolweerstand blijft vrijwel gelijk.
d Fnetto is nu 180 − 80 = 100 N.
De versnelling is dan
Fnetto ____
100
2
a = ____
m = 125 = 0,80 m/s
e Fnetto = 0 N
Als de scooter op topsnelheid rijdt, verandert zijn
snelheid niet. Er is dan geen netto kracht meer.
f Vlak voor Erik begon te remmen was de totale
weerstand 180 N. De totale weerstand als hij begint
te remmen is dus 180 + 500 = 680 N
De vertraging die hij krijgt is dus:
Fnetto ____
680
2
a = ____
m = 125 = 5,44 m/s
De vertraging wordt natuurlijk direct minder omdat
bij afnemende snelheid ook de weerstand kleiner
wordt. Maar bij dezelfde remkracht altijd minstens
500
____
2
125 = 4,0 m/s
29 a De snelheidsgrafiek gaat steeds steiler (naar
beneden) lopen. De vertraging neemt dus toe en de
remkracht ook.
b Je moet eerst de versnelling bepalen uit de raaklijn
bij t = 2 s.
De helling van die raaklijn is ongeveer − 2,5 m/s2
(vergeet niet de snelheid om te rekenen in m/s!).
Fnetto = m · a = 75 × 2,5 = 1,9 · 102 N
c Frem = 1,9 · 102 N
Omdat Suzanne op t = 2 s juist 20 km/h rijdt, weet
je dat dan de weerstand die zij ondervindt eveneens
25 N is. Omdat zij vertraagt met een netto kracht
van (onafgerond) 188 N moet de extra remkracht op
t = 2 s dus 188 − 25 = 163 N zijn.
30 a De motorkracht is dan wel voldoende om de raket
omhoog te laten gaan, maar ze willen eerst een paar tests
uitvoeren om zeker te weten dat alles goed functioneert.
b 3,04 · 106 − 7 × 12,9 · 103 = 2,95 · 106 kg
c De kracht die nodig is, is de stuwkracht min de
zwaartekracht:
34,8 − 28,9 = 5,0 · 106 N = 5,9 MN (meganewton).
Fnetto ________
5,9 · 106
2
d a = ____
m = 2,95 · 106 = 2,0 m/s
e 3,04 · 106 − 135 × 12,9 · 103 = 1,30 · 106 kg
f Fnetto = m · a = 1,30 · 106 × 29 = 37,7 · 106 N
De luchtweerstand is de stuwkracht min de netto
kracht:
Fw = 40,7 − 37,7 = 3,0 MN (meganewton).
(de stuwkracht lees je af in de grafiek)
42
242759_NAT 3E TF HAVO 4 UW_CH04.indd 42
F
3,0 · 106
= 1,04
g k = __w2 = ________
v
(1,7 · 103)2
N
h De eenheid is ____
= Ns2/m2. (delen door een breuk is
(m⁄s)2
vermenigvuldigen met het omgekeerde).
Omdat 1 N gelijk is aan 1 kg · m/s2 is dit te vereenvoudigen tot kg/m.
i Het frontale oppervlak. Een grotere raket vangt
meer wind.
j In dat geval werkt de zwaartekracht ook nog steeds
tegen. Een gedeelte van wat we nu als luchtweerstand berekend hebben is eigenlijk zwaartekracht.
Het antwoord is dus dat de weerstand kleiner is dan
berekend.
Als de raket schuin omhoog gaat werkt niet de hele
zwaartekracht het versnellen tegen, maar slechts een
deel ervan.
k De gemiddelde massa tijdens het ‘branden’ van de
tweede trap is 1,30 · 106 − 2,22 · 105 = 1,078 · 106 kg
(zie ook vraag e)
De snelheidstoename is 4,7 km/s, dus de versnelling
is:
4700
∆v = _____
= 13,06 m/s2
a = ___
∆t
360
Fnetto = m · a = 1,078 · 106 × 13,06 = 14 · 106 N
l Als de eerste trap is opgebrand dan wordt het
omhulsel afgestoten. De massa is dus kleiner dan
hierboven verondersteld is, en de netto kracht ook.
Bovendien wordt dat omhulsel zodanig weggeschoten dat de raket daardoor nog extra snelheid krijgt.
Dus de snelheidsverandering komt niet volledig
voor rekening van de stuwkracht.
31 a De massa neemt af.
De luchtweerstand neemt eerst toe en dan weer af.
De zwaartekracht neemt langzaam af.
b De enige oorzaak is dat de massa snel afneemt.
De luchtweerstand wordt in eerste instantie groter,
maar dat weegt niet op tegen de afname van de
massa. Pas als de raket kilometers gestegen is gaat de
luchtweerstand weer afnemen doordat de lucht ijler
wordt. De stuwkracht neemt dan ook toe, doordat de
uitgestoten verbrandingsgassen minder last hebben
van de luchtdruk.
De afname van de zwaartekracht gaat pas een rol
spelen op nog veel grotere hoogte.
32 a Volgens de gegevens in opdracht 30 heeft de raket
160 s nodig om een hoogte van 61 km te bereiken.
Volgens het model is dat ongeveer 140 s, dat ligt
aardig in de buurt.
Als je de snelheid gaat bekijken is het wat minder: na
135 s heeft de raket volgens opdracht 30 een snelheid
van 2,3 km/s. Als je een raaklijn tekent bij tijdstip 135 s,
vind je een snelheid van ongeveer 1,2 km/s.
b Door de vorm van de raket en de enorme massa
speelt de luchtweerstand niet de grootste rol in het
krachtenspel.
c Fres = Fm − Fz (Fm is de stuwkracht)
© Noordhoff Uitgevers bv
15/07/13 12:33 PM
Hoofdstuk 4 Kracht en beweging
33
34
Laat je werk controleren door je docent.
a Nee, want de stuwkracht neemt in werkelijkheid
niet lineair toe. De snelheid verandert daardoor ook
anders.
b Dan is in werkelijkheid de eindsnelheid veel hoger
dan volgens het model, maar de gemiddelde
snelheid niet. Dat betekent dat de snelheid in het
begin langzamer toeneemt dan volgens het model
en op het eind juist sneller. Op die manier leg je
dezelfde afstand af, maar met een hogere eindsnelheid.
c Met het feit dat de raket niet recht omhoog blijft
vliegen maar steeds meer horizontaal gaat. Het
model trekt de zwaartekracht gewoon van de
stuwkracht af, alsof ze op één lijn liggen.
d Fz moet uit het model verwijderd worden.
Er moet misschien rekening gehouden worden met
schuifwrijving (afhankelijk van de lanceeropstelling).
e Laat je werk controleren door je docent.
4.3 Zwaartekracht en massa
Fz = 1 × 9,81 = 9,81 N (newton)
35 a Je hangt een massa van exact 1 kg aan de krachtmeter. De zwaartekracht die je meet als de krachtmeter
stil hangt is getalsmatig even groot als de versnelling van de zwaartekracht.
Fz
Fz = m · g Dus g = __
m ofwel g = Fz
b Als bekend is hoe groot g is, kun je met een krachtFz
meter Fz bepalen en dan met m = __
g de massa
uitrekenen.
Nog slimmer is om de schaalverdeling zo aan te
passen, dat je direct de massa in kg afleest.
36 a 0 N
Op t = 0 s beweegt de parachutist nog niet. De
luchtweerstand is dan 0 N.
b 9,81 m/s2
Op t = 0 s geldt gewoon de versnelling voor een
vrije val: g = 9,81 m/s2.
Meet de helling van het eerste stukje van de grafiek
eens op!
c 7,8 · 102 N
De netto kracht op t = 0 s is gelijk aan de
zwaartekracht.
Dus Fnetto = Fz = m · g = 80 × 9,81 = 7,8 · 102 N
d 7,8 · 102 N
Als de snelheid constant is zijn de zwaartekracht en
de luchtweerstand aan elkaar gelijk, want Fnetto moet
0 zijn. De luchtweerstand is dus 7,8 · 102 N.
e 2 · 101 m/s2
Bepaal de helling van het steil dalende stuk van de
grafiek:
15 − 45 ____
−30
1
2
a = ______
19 − 17 = 2 = −15 = −2 · 10 m/s
Het minteken mag je weglaten vanwege het woord
‘vertraging’.
Doordat de tijd kort is en de grafiek klein is dit zeer
onnauwkeurig.
f 7,8 · 102 N
In dit geval geldt precies hetzelfde als bij d.
De luchtweerstand is dus weer 7,8 · 102 N.
© Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_CH04.indd 43
g Het gedeelte tussen 20 en 26 seconden is slechts
10 × 6 = 60 meter.
Eén seconde later zou al fataal zijn geweest.
37
Pulsje
38
C
Alle meetwaarden stellen hetzelfde voor, behalve C,
want 1 kg/m3 = 1 kg/1000 dm3 = 0,001 kg/dm3
Bedenk dat 1 L = 1 dm3 en 1 mL = 1 cm3 .
39 a 2,4 N
Je zoekt eerst in Binas de versnelling ten gevolge
van de zwaartekracht op Mars op: gMars = 3,7 m/s2
Deze g gebruik je om de zwaartekracht te
berekenen:
Fz = m · gMars = 0,64 × 3,7 = 2,368 = 2,4 N
b 6,8 kg
Fz __
25
m = __
g = 3,7 = 6,756… = 6,8 kg
40
9,79 m/s2
eerst de gegevens omrekenen:
2,54 notew = 2,54 × 3,06 N = 7,7724 N
1,000 kolie = 0,7938 kg
Fz ______
7,7724
2
g = __
m = 0,7938 = 9,79 m/s
41 a 2,3 kg
Fz = 20 N; gVenus = 8,88 m/s2
Fz ____
20
m = __
g = 8,88 = 2,252 = 2,3 kg
b/c De streep van 1 kg moet dus bij 8,88 N staan, en de
streep van 2 N bij 17,76 N; de rest van de strepen
moet gelijkmatig verdeeld worden.
Als je elke 0,2 kg een streep zet dan is de afstand
tussen de strepen 0,89 cm.
N
kg
0
2
4
6
8
10
12
14
16
18
20
0
0,2
0,4
0,6
0,8
1,0
1,2
1,4
1,6
1,8
2,0
2,2
N.B. De tekening is op schaal 1:2.
d 1,10 kg
9,81
keer zo groot als op
Op aarde is de valversnelling ___
8,88
9,81
___
Venus, dus geeft hij 8,88 × 1,00 kg = 1,10 kg aan.
Je kunt dat ook op de schaalverdeling zien: 1,00 kg
weegt op Aarde 9,81 N. Die 9,81 N staat op de
schaalverdeling naast 1,1 kg.
Dit klopt dus met de berekening.
e Een balans is overal zonder aanpassingen bruikbaar
om massa’s mee te bepalen, omdat een balans een
onbekende massa vergelijkt met een bekende.
43
15/07/13 12:33 PM
Hoofdstuk 4 Kracht en beweging
v
gummetje
45 a
4
snelheid in m/s
42 a Het eerste stukje van de grafieken is hetzelfde;
beide beginnen met een vrije val. Maar de prop
watten gaat sneller afwijken dan het gummetje.
3
2
1
0
–1
prop watten
–2
–3
–4
t
b
X1
gum
watten
t
c Het gummetje heeft een kleiner oppervlak dan de
even zware prop watten. Het ondervindt pas bij een
hogere (val)snelheid een luchtweerstand die even
groot is als zijn zwaartekracht.
43 a De massa
Deze brievenweger werkt als een balans.
b 51 gram
Dan moet je uitrekenen op welke massa de zwaartekracht 0,50 N is.
Fz _____
0,50
m = __
g = 9,81 = 0,051 kg = 51 gram
c Ja, op de maan geeft deze brievenweger ook de
juiste waarde. Het contragewicht weegt daar ook
zes keer minder, net als de brief. De massa’s worden
dus op een eerlijke manier met elkaar vergeleken.
44 a De krachtmeter en de balans geven beide correcte
meetwaarden.
In de schaalverdeling van de veerunster is de aardse
zwaartekrachtsversnelling verwerkt, dus die wijst
verkeerd aan.
b De zwaartekracht op de steen en zijn massa zijn
bekend. De valversnelling is dan eenvoudig te
berekenen met:
Fz _______
0,85
2
g = __
m = 0,0622 = 13,7 m/s
86,6
_____
× 9,81 ≈ 13,7 m/s2 mag ook.
622
c Balans: 62,2 g
Een balans vergelijkt massa’s en geeft dus overal
hetzelfde aan.
Krachtmeter:
Fz = m · gAarde = 0,0622 × 9,81 = 0,610 N
Veerunster: 62,2 g
De veerunster was immers geijkt op aarde en geeft
nu de juiste massa aan.
44
242759_NAT 3E TF HAVO 4 UW_CH04.indd 44
1
2
3
4
tijd in s
5
b 3,2 m/s
De gemiddelde snelheid is:
3,5
vgem = ___
2,2 = 1,59 m/s (het omhooggaande deel van de
sprong duurt even lang als het weer omlaag gaan,
dus 2,2 s)
De snelheid neemt tijdens de sprong gelijkmatig af
tot nul. De gemiddelde snelheid is dus de helft van
de maximale snelheid.
De beginsnelheid (maximumsnelheid) is dus:
vb = 2 × 1,59 = 3,18 m/s.
Met die snelheid kom je ook weer neer; je legt
dezelfde afstand terug af in dezelfde tijd.
c 1,4 m/s2
3,18
∆v = ____
= 1,445… = 1,4 m/s2
g = ___
∆t 2,2
46 a m2/s2 of (m/s)2
Eenheid van versnelling × eenheid van hoogte is
m/s2 × m = m2/s2
Dit is de eenheid van snelheid in het kwadraat.
Dat is omdat de bewegingsenergie evenredig is met
het kwadraat van je snelheid. Het risico is evenredig
met je bewegingsenergie. Zie hoofdstuk 7.
b 12 m
De valversnelling op de maan is 1,63 m/s2.
20 = 12 m
20 = 1,63 × h → h = ____
1,63
Zes keer zo groot als op aarde, omdat de valversnelling zes keer zo klein is.
c 0,80 m
De valversnelling op Jupiter is 24,9 m/s2.
20
h = ____
24,9 = 0,80 m
Jupiter is wel een gasplaneet, dus eigenlijk kun je niet
springen op Jupiter...
d Ja, want als de valversnelling kleiner is kun je hoger
springen.
Omhoog gaan kost dan minder energie per meter, je
komt dus hoger met dezelfde bewegingsenergie.
47 a 8,18 · 10 −6 m3
De straal r = 1,25 cm = 1,25·10 −2 m
Het volume is dan:
4
4
V = _3_ · π · r3 = _3_ · π · (1,25 · 10 −2)3 = 8,18 · 10 −6 m3
Het mag ook in cm3 , dan komt er 8,18 cm3 uit.
© Noordhoff Uitgevers bv
15/07/13 12:33 PM
Hoofdstuk 4 Kracht en beweging
b 0,064 kg
De dichtheid van staal is 7,8 · 103 kg · m −3
(hiervoor moet je kijken in de tabel met ‘alliages’,
want staal is geen zuivere stof maar een mengsel
van ijzer en o.a. koolstof)
m = · V = 7,8 · 103 × 8,18 · 10 −6 = 0,0638 kg
(= 64 gram)
c 3,6 cm
De dichtheid van aluminium is 2,70 · 103 kg·m −3
massa in kg
volume in m
3
2,70·103
0,0638
1,0
2,36·10−5
Het volume is dus 2,36 · 10 −5 m3
m)
(dat kan ook met V = __
4
__
−5
3
2,36 · 10 = 3 · π · r
r 3 = 5,64 · 10 −6 m3
r = 0,0178 m = 1,78 cm
de diameter is 2 × 1,78 = 3,56 = 3,6 cm
48 a Je doet wat water in een maatcilinder en leest het
volume af. Dan laat je het stukje metaal in het water
zakken en leest opnieuw af. Het verschil is het
volume van het stukje metaal.
Natuurlijk moet je zoveel water nemen dat het
voorwerp helemaal onder water komt. Verder gebruik
je een zo smal mogelijke maatcilinder; dat leest het
nauwkeurigst af.
b 47 g = 0,047 kg; 6,5 mL = 6,5 cm3 = 6,5 · 10 −6 m3
gebruik een verhoudingstabel:
massa in kg
0,047
volume in m
3
7,23 ∙ 103
6,5 ∙ 10
−6
1,0
dus de dichtheid is 7,2 · 103 kg/m3
of vul de formule in: m = · V
0,047 = × 6,5 · 10 −6 →
0,047
= _________
= 7,2 · 103 kg/m3
6,5 · 10 −6
Volgens Binas kan het zink of chroom zijn, maar
stukjes puur chroom kom je niet vaak tegen.
Als de meting niet al te nauwkeurig is komen ook tin
en gietijzer in aanmerking.
c De stukjes zijn even zwaar. Als het stukje sneller valt
dan een ronde kogel moet het een betere stroomlijn
hebben, bijvoorbeeld langwerpig met een spitse
punt.
49 a De dichtheid van vurenhout is 0,58 · 103 kg·m −3
en die van pvc is 1,3 · 103 kg·m −3.
De bal van pvc is dus 1,3 : 0,58 = 2,24 keer zo zwaar
als die van vurenhout.
Als de ballen hun maximale snelheid hebben bereikt
is de luchtweerstand even groot als de zwaartekracht. Bij de bal van pvc zijn beide krachten dus
2,24 keer zo groot als bij de houten bal:
© Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_CH04.indd 45
Fw
Fw
hout
pvc
Fz
Fz
b 1,5 keer zo groot
De constante k hangt alleen van de vorm af, dus die
is voor beide ballen hetzelfde.
Fw is bij het pvc 2,24 keer zo groot als bij het hout,
dus v2 ook.
____
Als v2 2,24 keer zo groot is, dan is v 2,24 = 1,5 keer
zo groot.
50 a 0,036 N
De dichtheid van helium bij de gegeven
temperatuur en druk is 0,178 kg·m −3.
9,5 L = 0,0095 m3, dus de massa van het helium is:
m = · V = 0,178 × 0,0095 = 1,69 · 10 −3 kg
(= 1,69 gram)
samen met de ballon en het touwtje is de massa dus
3,69 g = 3,69 · 10 −3 kg.
De zwaartekracht is dus:
Fz = m · g = 3,69 · 10 −3 × 9,81 = 0,0362 = 0,036 N
b 0,12 N
De dichtheid van de lucht is 1,293 kg·m −3. Omdat de
ballon ook 9,5 L lucht verplaatst is de massa hiervan:
m = · V = 1,293 × 0,0095 = 12,28 · 10 −3 kg
dus de zwaartekracht Fz = m · g = 12,28 · 10 −3 × 9,81 =
0,1205 = 0,12 N
c De netto kracht (stijgkracht) is dus 0,12 − 0,036 =
0,084 N
De versnelling is:
Fres _________
0,084
2
a = _____
m = 3,69 · 10 −3 = 22,76 = 23 m/s
d Die grote versnelling heeft hij maar heel even. Zodra
hij in beweging komt ontstaat er een tegenwerkende luchtweerstand. Omdat de stijgkracht zo klein is,
is de luchtweerstand al bij een lage snelheid even
groot als de stijgkracht. De stijgsnelheid blijft dan
verder constant.
4.4 Wisselwerking van krachten
51 a De boot zet zich af tegen de waterstraal.
b Een propeller zet zich af tegen de lucht.
c Een straalmotor zet zich af tegen een mengsel van
lucht en verbrandingsgassen.
45
15/07/13 12:33 PM
Hoofdstuk 4 Kracht en beweging
52
Ze waren bang dat de wisselwerkingkracht van de
kogels op het schip groot genoeg zou zijn om het
schip zo hard te bewegen dat mensen en spullen
omvallen. Als de lading van een schip begint te
verschuiven kan het schip kapseizen.
53
Pulsje
b In het eerste geval ondervindt de broek aan elke
kant de trekkracht van één paard; in het tweede
geval is dat de kracht van twee paarden, dus dubbel
zoveel.
65
Bij de start is er een grote versnelling en bij de
landing is de vertraging groot. Dat betekent dat er
grote krachten op je lichaam werken.
Tijdens de baan om de aarde werkt alleen de zwaartekracht op de astronauten en de raket; dan is de
versnelling van de raket even groot als die van de
astronauten. De raket hoeft dus niet tegen de
astronauten te duwen. Bij de landing en de start is
dat wel zo.
54 a 1 De richting is tegenovergesteld.
2 De ene werkt op voorwerp A, terwijl de ander op
voorwerp B werkt.
b De grootte van wisselwerkingskrachten is gelijk.
c Ze werken niet op hetzelfde voorwerp.
55 a De spijker hangt aan de magneet. Dus is er een
kracht op de spijker – anders zou hij vallen. Je kan
het magneetje ook aan de spijker laten hangen of
met de spijker de magneet opzij trekken. Er is dus
ook een kracht op de magneet.
b De spijker oefent ook een aantrekkingskracht uit op
de aarde.
56 a De auto is flink gekreukeld of gedeukt.
b De lantaarnpaal is kapot: omgeknakt of verbogen.
c Beide krachten zijn even groot.
57
De maan trekt ook de aarde aan. De wisselwerkingskracht van de zwaartekracht van de aarde op de
maan, is de zwaartekracht van de maan op de aarde.
58
Het gewicht en de normaalkracht. Het gewicht is de
kracht van de bal op de grond, de normaalkracht is
de kracht van de grond op de bal.
De wisselwerkingskracht van de zwaartekracht op de
bal is de aantrekkingskracht van de bal op de aarde.
59
De kracht die de bal op de veer uitoefent tijdens het
wegschieten.
60
De schuifweerstand van de tafel op de aarde.
De draaisnelheid van de aarde verandert hierdoor
tijdelijk en onmeetbaar weinig.
61 a Het gewicht is de kracht waarmee je tegen de grond
duwt.
b De wisselwerkingskracht die daarbij hoort is de
normaalkracht.
62
Gewicht; je duwt immers nergens op.
Als de zwaartekracht nul was zou je niet vallen.
63
Omdat je tegelijkertijd het zadel naar achteren duwt.
64 a In het eerste plaatje is er aan elke kant de kracht van
één paard.
In het tweede plaatje is er rechts de kracht van twee
paarden, maar zolang de broek op zijn plaats moet
er een even grote kracht naar links zijn.
Het paaltje ‘trekt dus terug’: het wordt vervormd
waardoor een veerkracht ontstaat die even groot is
als de trekkracht van de twee paarden.
46
242759_NAT 3E TF HAVO 4 UW_CH04.indd 46
66 a De vlotten komen in beweging, naar elkaar toe.
Omdat team Groen lichter is dan Blauw gaat team
Groen sneller (met een grotere versnelling) naar
Blauw dan andersom.
b Dan gebeurt hetzelfde. Als team Groen zich alleen
maar schrap zet om niet uit balans te raken, trekt
het ongemerkt toch even hard terug.
67
Bij de letters remmen de auto’s meestal. Het
wegdek duwt dan de wielen naar achteren en de
wielen duwen het wegdek en de letters naar voren.
Bij de streep trekken de auto’s meestal op: de wielen
duwen het wegdek en de letters naar achteren en
het wegdek duwt de wielen naar voren.
68 a
F op Aad
F op het karretje
F op de grond
b Het karretje moet een netto kracht naar voren
ondervinden, dus de duwkracht van Aad moet
groter zijn dan de weerstandskrachten op de wielen.
c Alle krachten zijn wisselwerkingen. Elk tweetal
krachten die in het zelfde punt werken, tegengesteld gericht zijn en verschillend gekleurd zijn,
vormen een wisselwerkingspaar. Alleen de wisselwerkingskrachten bij de zwaartekracht op Aad en
op de kar zijn niet getekend. Die krachten werken
namelijk op het zwaartepunt van de aarde.
69 a De normaalkracht van de tafel op de appel.
b D
© Noordhoff Uitgevers bv
15/07/13 12:33 PM
Hoofdstuk 4 Kracht en beweging
70 a
73 a 1,7 · 102 N
Eerst de versnelling uitrekenen:
∆v = ___
12 = 3,0 m/s2
a = ___
∆t 4,0
b
c
d
e
De aandrijfkracht is de kracht die het wegdek
uitoefent op het achterwiel, als het wiel de weg
naar achteren duwt.
24 N
De aandrijfkracht = totale weerstandskracht.
F = 14 + 10 = 24 N.
120 N
Bij het berekenen van de netto kracht gebruik je de
totale massa: Fnetto = mtot ·a = 80 × 1,2 = 96 N
Omdat de totale weerstand 24 N is moet de
aandrijfkracht 96 + 24 = 120 N zijn.
52 N
De trekhaak versnelt alleen de kar; nu gebruik je
alleen de massa van de kar en de weerstandskracht
op de kar:
Fnetto = mkar ·a = 35 × 1,2 = 42 N
omdat de weerstand op de kar 10 N is moet de
trekkracht 42 + 10 = 52 N zijn.
Ook 52 N.
Volgens de derde wet van Newton oefenen de fiets
en de kar een even grote kracht op elkaar uit.
De netto kracht op de fiets (zonder kar) is nu
120 − 52 − 14 = 54 N. Klopt dat met de tweede wet van
Newton?
71 a 1,4 · 102 N
216 = 60 m/s
∆v = ___
3,6
60 = 2,4 · 103 m/s2
∆v = _____
a = ___
∆t 0,025
Fnetto = m · a = 0,057 × 2,4 · 103 = 1,4 · 102 N
Bij deze berekening doen we alsof de kracht en de
versnelling constant zijn; in werkelijkheid is dat niet
zo, dus is de uitkomst de gemiddelde kracht.
b 11 m/s
De kracht van de bal op het racket is ook 1,4 · 102 N,
dus:
1,4 · 102
F _______
2
2
a = __
m = 0,300 = 4,56 · 10 m/s
∆v = a · ∆t = 4,56 · 102 × 0,025 = 11 m/s
c Als je de massa van de bovenarm maar half meetelt
is de totale massa 0,3 + 0,3 + 1,0 + 1,0 = 2,6 kg.
De massa is dan ruwweg 9 keer zo groot, waardoor
de snelheidsverandering 9 keer zo klein is: ruim
1 m/s.
d De wisselwerkingkracht van de bal op je racket
heeft minder effect op de snelheid van je racket
waardoor je meer controle hebt.
Je kunt (aan het net) minder snel reageren omdat je
racket langzamer in beweging komt.
72
Dan de netto kracht:
Fnetto = m · a = 58 × 3,0 = 174 = 1,7 · 102 N
b 76 kg (als we aannemen dat de lift omhoog gaat)
Om dit op te kunnen lossen moet je beseffen dat:
- de netto kracht op de passagier omhoog gericht is,
- die netto kracht ontstaat doordat de normaalkracht groter is dan de zwaartekracht*;
- de weegschaal in feite meet hoe hard de passagier
op de schaal duwt, dat is dus het gewicht, en dat
‘omrekent’ naar kilogram,
- het gewicht even groot is als de normaalkracht,
want deze twee vormen een wisselwerkingspaar.
De zwaartekracht is 58 × 9,81 = 569 N.
Om een netto kracht van 174 N omhoog te krijgen
moet de normaalkracht dus 174 N groter zijn dan de
zwaartekracht: Fn = 569 + 174 = 743 N
Het gewicht is dus ook 743 N; daarbij hoort een
743
= 75,7 = 76 kg
massa van ___
9,81
Pulsje
* Als de lift versneld omhoog gaat blijft de passagier
door zijn traagheid nog even achter, daardoor vervormt
de vloer van de lift en ontstaat een extra normaalkracht.
Die is dan dus groter dan wanneer de lift niet versnelt.
c 58 kg
Nu is de netto kracht nul en de normaalkracht gelijk
aan de zwaartekracht. Ook het gewicht is dan gelijk
aan de zwaartekracht: 569 N. Daarbij hoort een
massa van 58 kg.
Toepassing
Opgave 1 Winterpret
1
In de formule zie je dat Fschuif evenredig is met Fz. Bij
een zwaarder voorwerp hoort een grotere Fz
waardoor Fschuif ook groter is.
2
Fschuif en Fz hebben allebei de eenheid newton, dus
is een getal zonder eenheid.
Fschuif
Formeel opgeschreven: = ____
Fz
__
N
dus eenheid van = = 1
N
Een getal zonder eenheid heet ‘dimensieloos’.
3
39 m
2,0 ton is 2,0 · 103 kg,
dus Fz = 2,0 · 103 × 9,81 = 19,62 kN,
Fschuif = Fz = 0,25 × 19,62 · 103 = 4,9 · 103 N
Fschuif _______
4,9 · 103
2
a = _____
m = 2,0 · 103 = 2,45 m/s
50 km/h = 13,89 m/s
13,89
∆v = _____
∆t = ___
a
2,45 = 5,67 s
vgem = 25 km/h = 6,94 m/s
S = vgemt = 6,94 × 5,67 = 39,36 = 39 m
Je kunt het wat compacter opschrijven:
mg
Fschuif ___
Fz _____
2
a = _____
m = m = m = g = 0,25 × 9,81 = 2,45 m/s
De uitkomst is dus onafhankelijk van de massa.
© Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_CH04.indd 47
47
15/07/13 12:33 PM
Hoofdstuk 4 Kracht en beweging
4
Zoals je ziet in de uitwerking van 3, kun je de massa
wegstrepen. De massa doet er dus niet toe.
5
9,0 N
Fz = 92 × 9,81 = 902,5 N
Fschuif = Fz = 0,010 × 902,5 = 9,0 N
Korter: Fschuif = mg = 0,010 × 92 × 9,81 = 9,0 N
6
32 km/h
Fnetto _____
9,025
2
a = ____
m = 92 = 0,0981 m/s
Probleem is hier dat je de tijd en de beginsnelheid
niet weet, dus ook niet de gemiddelde snelheid; hier
kom je alleen uit als je formules gaat combineren: je
weet dat:
s
__
__
1
1
∆v = a · ∆t, ∆t = ____
v en vgem = 2 vbegin = 2 ∆v want de
10
De rolweerstand en de motorkracht zijn constant;
de motorkracht is natuurlijk de grootste, anders kan
hij niet rijden. Dus groen is de motorkracht en zwart
de rolweerstand.
De luchtweerstand hangt kwadratisch af van de
snelheid, dat is de rode grafiek.
De netto kracht is het verschil tussen de motorkracht en de totale weerstandskracht, dat is de
blauwe grafiek.
11
4,0 N
Raaklijn tekenen op t = 0 s en de helling bepalen:
10 = 1,82 m/s2
∆v = ___
a = ___
∆t 55
F = ma = 1,82 × 2,2 = 4,0 N
12
De snelheid is dan nog klein en dus de luchtweerstand ook.
Fnetto is 4,0 N, de motorkracht is 5,0 N, dus de
rolweerstand is 1,0 N.
De luchtweerstand hangt van het kwadraat van de
snelheid af. Als je een klein getal kwadrateert wordt
het nog kleiner.
13
1,4 N
Op t = 6,0 s is de snelheid 8,0 m/s.
Fl = 0,040 × 8,02 = 2,56 N
Fnetto = 5,0 − 1,0 − 2,56 = 1,4 N
14
De netto kracht is nul als de snelheid constant is.
De luchtweerstand moet dan 4,0 newton zijn.
Aangezien de eindsnelheid 10 m/s is geldt dan:
4,0
k = ___2 = 0,040 Ns2/m2
10
gem
eindsnelheid is nul
s
s
2s
____
___
dus ∆v = a · ∆t = a · ____
vgem = a · __1 ∆v = a · ∆v
2
hieruit volgt ∆v2 = a · 2s = 2as = 2 × 0,0981 × 400 =
78,48 dus ∆v = 8,86 = 8,9 m/s en dat is ook de
beginsnelheid. 8,9 m/s = 8,9 × 3,6 = 32 km/h
De versnelling kun je ook uitrekenen met:
a = g = 0,010 × 9,81 = 0,0981 m/s2
In hoofdstuk 7 zullen we zien dat dit probleem ook op
een gemakkelijkere manier op te lossen is.
7
0,89 m/s2
In totaal is er dan 9,0 + 73 = 82 N weerstand, dat is
ook de netto kracht. De vertraging is dan
Fnetto ___
82
2
a = ____
m = 92 = 0,89 m/s
In het begin is de luchtweerstand groot en die
neemt snel af, dat geldt ook voor de vertraging.
v
8
Opgave 3 Een kist met zwaartekracht
15
Zolang de snelheid nog niet constant is, is de
zwaartekracht het grootste.
Tijdens het vallen worden de kisten alleen ‘ondersteund’ door de luchtweerstand en die is in het
begin kleiner dan de zwaartekracht. Dus is de kracht
van de kisten op de lucht, hun gewicht, ook kleiner
dan de zwaartekracht.
Als de snelheid constant is geworden zijn de luchtweerstand en het gewicht weer even groot als de
zwaartekracht.
16
t
Opgave 2 Radiografisch bestuurbare auto
9
27 m
Oppervlaktemethode toepassen:
Maak een eerlijke driehoek en bereken het oppervlak met een half maal basis maal hoogte
1
s = __
2 b · h = 0,5 × 6,0 × 9,0 = 27 m
48
242759_NAT 3E TF HAVO 4 UW_CH04.indd 48
De luchtweerstand is de kracht van de lucht op de
kisten. De bijbehorende wisselwerkingskracht is de
kracht die de vallende kisten op de lucht uitoefenen.
Dat is dus hun gewicht.
De luchtweerstand heeft hier de functie van normaalkracht, die ‘ondersteunt’ de kisten.
© Noordhoff Uitgevers bv
15/07/13 6:05 PM
Hoofdstuk 4 Kracht en beweging
17
Als de helikopter op de bodem staat drukt zijn
gewicht op de bodem. Als de helikopter vliegt drukt
zijn gewicht op de (neerdalende) lucht. Die drukt
dan weer met een even grote kracht op de bodem.
Het gewicht van de kist blijft daardoor gelijk:
Flucht op heli
24
Opgave 5 Ariane-5-raket
25 Volgens de derde wet van Newton geeft de neerwaartse kracht op de uitgestoten verbrandingsgassen een even grote opwaartse kracht op de raket.
26
Fheli op lucht
Fz
Fkist op lucht
Flucht op kist
Opgave 4 Archimedes
18 De dichtheid van ijs is kleiner dan de dichtheid van
zeewater. Omdat de dichtheid van het ijs kleiner is
blijft het drijven.
19
Omdat m = · V is:
FA = Fz,vloeistof = mvloeistof · g = · V · g
20
De eenheid van FA is eenheid van dichtheid ×
eenheid van versnelling × eenheid van volume =
kg m
kg __
m
___
× × m3 = _____
m3 s2
s2
Eén newton is de kracht die nodig is om één
kilogram met één meter per secondekwadraat te
kg m
versnellen. Dus 1 ____
s2 = 1 N
21
9,4 MN
FA = 1024 × 9,81 × 9,0 · 103 = 90,4 × 106 N
Fz = 917 × 9,81 × 9,0 · 103 = 81,0 · 106 N
dus FA − Fz = (90,4 − 81,0) · 106 = 9,4 · 106 N
22
De stijgkracht is de netto kracht. Het ijsblok ligt stil
dus de stijgkracht is nul.
23
90%
De Archimedeskracht is nu gelijk aan de zwaartekracht: FA = Fz
1024 × 9,81 × Vwater = 917 × 9,81 × Vijs
917 × 9,81
Vwater = __________ Vijs = 0,896 × Vijs
1024 × 9,81
Dus 90% zit onder water.
© Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_CH04.indd 49
11 MN
Eerst de versnelling bepalen d.m.v. een raaklijn op
t = 0 s; de helling daarvan is:
600 = 6,0 m/s2
∆v = ____
a = ___
∆t 100
dus Fnetto = m · a = 7,14 · 105 × 6,0 = 4,284 · 106 N,
en Fz = m · g = 7,14 · 105 × 9,81 = 7,004 · 106 N
Fstuw = Fnetto + Fz = 4,284 · 106 + 7,004 · 106 =
11,29 · 106 N = 11 MN
Korter:
Fstuw = Fnetto + Fz = m(a + g)
= 7,14 · 105 × (6,0 + 9,81)
= 11 MN
Fn op kist
kracht op helikopter (getrokken lijn)
kracht op lucht (stippellijn)
kracht op kist (streepjeslijn)
Het zou minder ver uitsteken omdat de dichtheid
van zoet water kleiner is. Het blok moet dan meer
water verplaatsen om de benodigde
Archimedeskracht te krijgen, dus dieper in het water
liggen.
27
In het begin neemt de luchtweerstand toe vanwege
de toenemende snelheid, daarna neemt de luchtweerstand weer af omdat de atmosfeer steeds ijler
wordt.
28
Groter vanwege twee redenen:
1 De massa is afgenomen omdat er minder brandstof over is.
2 De luchtweerstand is kleiner geworden.
De zwaartekracht neemt langzaam af als je van de
aarde af beweegt, maar op 100 km hoogte is dit
effect nog erg klein.
29
14 km
Oppervlaktemethode. Een driehoek van 450 m/s
hoog en 60 s breed benadert de oppervlakte heel
aardig. De oppervlakte daarvan is:
0,5 × 60 × 450 = 13500 m = 14 km
30
Laat je werk controleren door je docent.
Opgave 6 Herbert James Munro
31
Volgens tabel 5 is een landmijl 1,609 km. De snelheid is dus 1,609 × 205,67 = 330,9 km/h
32
Dat is de enige plaats met zo een lange vlakke
horizontale ondergrond.
Omdat hij langzaam optrekt legt hij veel afstand af,
een bocht maken kost snelheid.
33
De druppelvorm heeft een goede stroomlijn en dus
een lage luchtweerstand.
34
Er is drie keer geschakeld, dus hij heeft tenminste
vier versnellingen.
49
15/07/13 12:33 PM
Hoofdstuk 4 Kracht en beweging
35
17,5 s
Volgens de grafiek is de topsnelheid 92 m/s (volgens
de gegevens 91,92 m/s), dus
1609
s _____
t = __
v = 92 = 17,5 s
36
Na 52,5 s
In de grafiek zie je dat hij meer dan 20 s op topsnelheid heeft gereden, dus hij heeft de hele flying mile
met 92 m/s gereden. Dus kwam hij op tijdstip t =
70 − 17,5 = 52,5 s langs de eerste controle.
37
Ongeveer 5 minuten
20 km/h ≈ 12,5 mijl/h = 0,2 mijl/min
dus ongeveer vijf minuten.
38
De luchtweerstand wordt steeds groter, totdat de
netto kracht nul is.
39
De luchtweerstand neemt weer af, waardoor de
vertraging ook afneemt.
40
De motorkracht moet in het begin groter zijn dan de
weerstand, anders komt de motor niet van zijn plek.
Bovendien wordt de (lucht)weerstandskracht almaar
groter door de toenemende snelheid, de motorkracht
wordt in de hogere versnellingen kleiner door de
veranderende overbrengingsverhouding van de
tandwielen.
41
De snelheid wordt na ongeveer 48 s constant, dan is
de netto kracht nul, dus de aandrijvende kracht is
even groot als de weerstand.
42
Tot t = 70 s blijven beide krachten constant. Daarna
wordt de motorkracht nul en neemt de weerstandskracht af door de dalende snelheid.
v
gummetje
prop watten
t
__________ weerstandskracht
_ _ _ _ _ _ _ motorkracht
Proefwerkopgaven
1 a Direct na het springen is de zwaartekracht groter
dan de luchtweerstand.
Als de snelheid constant is zijn beide krachten even
groot.
b De luchtweerstand, want de parachutist remt dan
af.
c De netto kracht is dan 0 N. De snelheid verandert
namelijk niet.
d In beide situaties is de luchtweerstand even groot.
In beide gevallen is de snelheid constant. De
luchtweerstandskracht bij ongeopende parachute
en hoge snelheid is gelijk aan de zwaartekracht. De
luchtweerstand bij geopende parachute en lage
snelheid is dat ook.
In het laatste geval is de snelheid veel lager, maar de
oppervlakte veel groter, waardoor de luchtweerstand
toch even groot is.
2 a 7,4 · 102 N
Omdat het gaat over de kracht op de caravan bekijk
je alleen de caravan.
Fnetto = mcaravan · a = 800 × 0,80 = 640 N
Als hij net wegrijdt is de luchtweerstand nog nul. De
rolweerstand is 100 N.
Dus moet de trekkracht 740 N zijn.
b 2,0 · 102 N
80 km/h = 22,22 m/s; de luchtweerstand is dus nu
0,21 × 22,222 = 104 N
De netto kracht is nul (constante snelheid) dus de
trekkracht is gelijk aan de totale weerstandskracht:
100 + 104 = 204 = 2,0·102 N.
c Ze wordt juist naar voren geduwd. Ze komt iets
minder snel op gang dan de auto. Ze blijft dus een
beetje achter, totdat haar stoeltje haar ‘meeneemt’.
Fnetto _____
10
d m = ____
a = 0,80 = 12,5 = 13 kg
e Die zijn onder alle omstandigheden even groot en
tegengesteld gericht, volgens de derde wet van
Newton.
3 a 0,631 m/s2
s = 1,00 m t = 1,78 s
1,00
vgem = _s =_____ = 0,562 m/s
t 1,78
omdat de beginsnelheid nul is, is de eindsnelheid
2 × 0,562 = 1,12 m/s, en de snelheidsverandering
ook, dus:
1,12
∆v = ____
= 0,631 m/s2
a = ___
∆t 1,78
b 0,170 N
Fnetto = mtotaal · a = (0,250 + 0,020) × 0,631 = 0,170 N
50
242759_NAT 3E TF HAVO 4 UW_CH04.indd 50
© Noordhoff Uitgevers bv
15/07/13 12:33 PM
Hoofdstuk 4 Kracht en beweging
c 8,5 m/s2
De netto kracht op het geheel is de zwaartekracht
op het hangende blokje.
Fz = Fnetto ⇒ m · g = 0,170 N
0,170
2
g = ______
0,020 = 8,5 m/s
d 0,026 N
De zwaartekracht op het blokje is:
Fz = m · g = 0,020 × 9,81 = 0,196 N
de netto kracht is slechts 0,170 N, dus moet er een
weerstandskracht zijn van 0,196 − 0,170 = 0,026 N
4 a hoogte(t) = hoogte(t-dt) − snelheid*dt
snelheid(t) = snelheid(t-dt) + versnelling · dt
resulterende kracht = zwaartekracht −
luchtweerstand
bovendien moeten er startwaarden bij voor de
hoogte en de snelheid:
hoogte = 3800
snelheid = 0
b De oppervlakte:
frontaal_oppervlak = 58
met als voorwaarde:
als h<1000
De cw waarde verandert waarschijnlijk ook, maar die
is niet behandeld. Dat is een constante die de stroomlijn aangeeft.
© Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_CH04.indd 51
51
15/07/13 12:33 PM
Hoofdstuk 5 Eigenschappen van stoffen
Hoofdstuk 5
Eigenschappen van stoffen
1
2
Introductie
1
a Juist. Water en ijs zijn twee toestanden van dezelfde
stof.
b Onjuist. Tussen de moleculen zit niets.
c Onjuist. Wolken bestaan uit kleine waterdruppeltjes.
Bereken eerst het volume van 1 pingpongballetje:
4 3 __
4
−3 3
−5
3
V = __
3 πr = 3 π × (20 · 10 ) = 3,35 · 10 m
2
In vacuüm zijn geen deeltjes aanwezig. De temperatuur is een maat voor de bewegingsenergie van de
deeltjes. Als er geen deeltjes zij heeft het ook geen
zin te spreken over temperatuur.
In 1 m3 passen dan 1/3,35 · 10 −5 = 29851 = 3,0 · 104
pingpongballetjes. Maar je kunt niet alles opvullen.
Er blijft ruimte over tussen de balletjes. Volgens
π
___
Gauss kun je maar 3 __2 = 0,74 deel opvullen. In 1 m3
passen dus maximaal 0,74 × 29851 = 2,21 · 104
pingpongballetjes.
3
4
5
5.1 Het deeltjesmodel
De hoeveelheid water is 81 maal gehalveerd en dat
levert 1 molecuul water op. De oorspronkelijke
hoeveelheid moleculen is dan 281 = 2,42 · 1024
watermoleculen.
De straal van de aarde is 6,378 · 106 m (Binas tabel 31).
Reken vervolgens de oppervlakte A uit van de aarde:
A = 4 πr 2 = 4 π (6,378 · 106)2 = 5,112 · 1014 m2.
Een laag op aarde van 1 m hoogte geeft een totaal
volume van 5,112 · 1014 × 1,000 = 5,112 · 1014 m3.
In 1 m3 zitten 2,21 · 104 pingpongballetjes en in
5,112 · 1014 m3 zitten 5,112 · 1014 × 2,21 · 104 = 1,13 · 1019
pingpongballetjes.
Het totaal aantal pingpongballetjes is gelijk aan
2,42 · 1024. Zie vraag 1. In een laag van 1,0 m dikte
zitten 1,13 · 1019 pingpongballetjes. De totale laagdikte wordt dan: 2,42 · 1024/1,13 · 1019 = 2,14 · 105 m =
214 km!
Boven 1 m2 aardoppervlak zit een laag van 214 km
pingpongballetjes. In 1 m3 zitten er 2,21 · 104. Boven
1 m2 aardoppervlak bevinden zich 2,21 · 104 × 214000 =
4,73 · 109.
6
De massa van die 4,73 · 109 pingpongballetjes is
4,73 · 109 × 0,0027 = 1,3 · 107 kg.
7
Het gewicht van 1,3 · 107 kg is 1,3 · 107 × 9,81 = 1,3 · 108 N.
De druk wordt dan: p = F/A = 1,3 · 108/1 = 1,3 · 108 N/m2.
8
1,0 bar = 1,0 · 105 N/m3. De druk door het gewicht
van de balletjes is dan: 1,3 · 108/1,0 · 105 = 1,3 · 103 bar.
9
Neem als straal van het bolletje: 1 cm. Het volume
van het bolletje is dan 4/3 π r 3 = 4/3 π × 13 cm3 =
4,19 cm3.
Het volume van het kubusje waar het bolletje
precies in past is 2 × 2 × 2 = 8 cm.
De bolletjes vullen dus 4,19/8 = 0,52 = 52% van de
beschikbare ruimte.
52
242759_NAT 3E TF HAVO 4 UW_CH05.indd 52
3 a Juist. De deeltjes hebben zelf geen volume.
b Onjuist. Bij temperatuurstijging neemt de snelheid
van de moleculen toe. Bovendien bewegen niet alle
moleculen even snel. Bij botsingen wordt snelheid
van het ene molecuul overgedragen naar het
andere.
c Onjuist.
4 a Juist. De vanderwaalskrachten werken alleen als de
afstand tussen de moleculen klein is.
b Onjuist. Bij een ideaal gas houd je alleen rekening
met afstotende krachten bij botsingen.
c Onjuist. Bij een ideaal gas is er geen aantrekkende
kracht tussen de moleculen en de afzonderlijke deeltjes kunnen dan ook niet ‘samenklonteren’ tot een
vloeistof.
5 a In 1 m2 zitten 100 × 100 = 10000 cm2.
De 50 N op die 1 m2 wordt verdeeld over 10000 cm2.
De kracht op 1 cm2 is dan 50/10000 = 0,0050 N.
De druk is dan 0,0050 N/cm2.
b Die druk is 3 · 104 Pa (Binas tabel 30F).
6 a 8,6 · 104 Pa
F m · g 7,0 x 9,81
p = __z = _____ = _________
= 8,6 · 104 Pa = 0,86 bar
A
A
8,0 · 10 −4
of:
F
7,0 x 9,81
p = __z = _________ = 8,6 N/cm2 = 0,86 bar
A
8,0
b Omdat er onder de zuignap ook nog wat lucht zit;
het drukverschil moet 0,86 bar zijn dus de buitenluchtdruk moet hoger zijn dan 0,86 bar.
7 a 1,2 · 105 N
F ⇒ F = pA = 1,0 · 105 × 1,2 = 1,2 · 105 N.
p = __
A
b Omdat ook aan de onderkant van het tafelblad een
druk heerst van 1,0 · 105 N/m2. De kracht van de
luchtdruk tegen de onderkant van het tafelblad is
dus ook 1,2 · 105 N.
© Noordhoff Uitgevers bv
15/07/13 12:34 PM
Hoofdstuk 5 Eigenschappen van stoffen
8
9
c De afwijking kan dan veroorzaakt zijn door de lucht
die in de slang en in de manometer zit.
d
volume V in
1/p
cm3
Het gewicht van de jongedame is 60 × 9,81 = 589 N.
80 % van dat gewicht rust op beide naaldhakken
met een oppervlakte van 2,0 cm2 = 2,0 · 10 −4 m2.
De druk is dan:
470
F = ________
= 2,4 · 106 Pa
p = __
A 2,0 · 10 −4
De druk onder de olifantenpoot is
1000 × 9,81
F = __________
= 24525 N/m2 = 25 kPa.
p = __
0,40
A
De druk onder de naaldhakken is bijna 100 keer groter!
Pulsje
10 a (druk × volume)grond = (druk × volume)hoogte
1 bar × 2,0 m3 = 0,30 bar × V
V = 2,0/0,30 = 6,7 m3.
b Je moet aannemen dat de temperatuur constant
blijft.
c De temperatuur zakt van 288 K naar 223 K op 10 km
hoogte waar de druk 30% is van de druk op zeeniveau. Dat is een daling van de temperatuur van 23%.
De aanname is dus niet terecht.
druk in bar
13 a p · V is hier niet constant. Als het volume bijvoorbeeld vijf keer kleiner wordt (van 25 naar 5) moet de
druk vijf keer groter worden en die wordt 3,86 keer
groter (van 1,00 naar 3,86).
b
4
1,5
1
0,5
0
0
10
20
30
40
volume in cm3
0,81
15
0,63
10
0,44
5
0,26
y = 0,0372x + 0,0711
R2 = 1
1,00
0,50
0
0
10
20
30
40
e Als het volume 0 cm is moet volgens de wet van
Boyle de druk p oneindig groot zijn en 1/p is dan 0.
1/p is echter iets groter dan nul en het gasvolume is
dan ook nog geen 0 cm3. Alleen gaat de grafiek niet
door nul; blijkbaar zijn alle volumes iets groter dan
je denkt. De lijn snijdt de x-as bij een volume
van − 2 cm3. Er zit dus 2 cm3 lucht in de slang en de
manometer. Dat komt door het volume van de
manometer en de slang. De lucht in de spuit
gedraagt zich wel als een ideaal gas.
3
14 a Een andere vaste stof die zich gedraagt als een zeer
trage vloeistof is glas.
b De fles met pek doet er ongeveer 180 jaar over om
leeg te stromen. Dat ronden we af op 200 jaar. Dat
zijn 200 × 356 × 24 × 60 × 60 = 6151680000
seconde. Water is 100 miljard maal minder stroperig
en een fles water zou 100 miljard maal eerder leeg
moeten zijn: 6151680000 : 100 000 000 000 =
0,06 s. Dat is wel heel snel voor een fles om leeg te
lopen. Conclusie het is niet recht evenredig.
16
2
20
1,50
15
2,5
1,00
2,00
3,5
3
1,56
25
Het verband tussen 1/p en V is lineair. Zie het
diagram hieronder:
11 a De tijd bereken je met: tijd = afstand/snelheid =
10/500 = 0,020 s.
b Door botsingen met andere moleculen is de baan
van het stikstofmolecuul zeker geen rechte lijn.
12 a 4,0 bar
hij kan de inhoud van zijn longen verkleinen tot
6,0 – 4,5 = 1,5 L, dat is vier keer zo klein; dan wordt
de druk dus vier keer zo groot: 4,0 bar
in formulevorm:
p1 · V1 = p2 · V2 → 1 × 6,0 = p2 × 1,5 → p2 = 4,0 bar
b 5,0 L
hij kan de druk maar 1,2 keer zo groot maken, dus
het volume 1,2 keer zo klein:
6,0 L : 1,2 = 5,0 L
in formule:
p1 · V1 = p2 · V2 → 1 × 6,0 = 1,2 × V2 → V2 = 5,0 L
Zie Binas tabel 83B.
40
5.2 Uitzetting
A Juist
B Juist
0,012 mm
Een spoorstaaf van 16 m die 1,9 mm langer wordt bij
een temperatuurstijging van 10 °C. Wordt 10 keer
minder langer bij een temperatuurstijging van 1 °C:
0,19 mm. Is de staaf dan ook nog eens 16 keer korter
(van 16 m naar 1,0 m) dan is de uitzetting ook 16 keer
kleiner: 0,19 mm /16 = 0,012 mm.
Het blauwe diagram is van de meetgegevens en het
rode diagram is van de waarden die je zou verwachten uitgande van de meting bij 1 bar.
© Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_CH05.indd 53
53
15/07/13 12:34 PM
Hoofdstuk 5 Eigenschappen van stoffen
17
7,6 cm
De lineaire uitzettingscoëfficiënt van staal is
0,000012 per °C. Per graad stijging wordt de
Eiffeltoren 0,000012 × 317 = 0,0038 m langer. Stijgt
de temperatuur 20 °C dan is de uitzetting 0,0038 ×
20 = 0,076 m = 7,6 cm.
18 a De temperatuur is gestegen omdat de staaldraad nu
langer is dan de invar draad.
b 22 °C
Bij elke graad stijging wordt de invar draad 30 ×
2,3 · 10 −6 = 0,000069 m langer.
Bij elke graad stijging wordt de staaldraad 30 ×
0,000012 = 0,00036 m langer.
Bij elke graad stijging wordt de staaldraad dus
0,00036 – 0,000069 = 0,00029 meter langer dan
de draad van invar. De staaldraad is 42 mm = 0,042
m langer geworden dan de invar draad. De temperatuurstijging is 0,042/0,00029 = 14 °C. De nieuwe
temperatuur is dan 10 °C + 14 °C = 24 °C.
19
23 a Het kookpunt van water is 373 K.
b Het smeltpunt van aluminium is 933 K en dat komt
overeen met 933 − 273 = 660 °C.
c Stikstof wordt vloeibaar bij 77 K en dat is −196 °C.
Het klopt dus niet.
24
– 273 °C
Het volume neemt af van 1000 naar 732 mL. Dat is
een ∆V van 268 mL. Daarbij hoort een temperatuurdaling van 100 °C.
Per 1 ml afname van het volume daalt de temperatuur 100/268 = 0,373 °C.
Het volume moet nog met 732 mL afnemen: de
temperatuur moet nog 732 × 0,373 = 273 °C dalen.
Conclusie: bij −273 °C is het gasvolume 0 mL.
25
21 cm3
De lineaire uitzettingscoëfficiënt van koper is
16,8 · 10 −6 per K. De kubieke uitzettingscoëfficiënt is
dan 3 × 16,8 · 10 −6 = 50,4 · 10 −6 per K.
De straal van de koperen bol is 10 cm.
4
4
Het volume is _3_ πr 3 = _3_π103 = 4189 cm3
In vullen in ∆V = V0 ∆T geeft als resultaat:
∆V = 50,4 · 10 −6 × 4189 × 100 = 21 cm3.
26
pulsje
0,0038 K−1
De gegevens waarmee het diagram is gemaakt op
een rijtje:
bij 0 °C
bij 100 °C
∆T = 100 °C
V0 = 720 mL
V = 1000 mL
∆V = 280 mL
Vul de gegevens in in de formule (1 mL = 1,0 · 10 −3 L):
∆V = V0 ∆T
280 · 10 −3 = × 720 · 10 −3 × 100
280 · 10 −3
· 10 −3
________
= _____________
= 280
73,2 = 0,0038
720 · 10 −3 × 100
= 0,0038 K−1
20
pulsje
21
5,5 · 102 m3
De gegevens op een rijtje:
V0 = 15000 m3
Tbegin = 80 °C en Teind = 90 °C en dus V = 10 °C
Invullen in: V = V0 T
∆V = 0,00367 × 15000 × 10 = 550,5
∆V = 5,5 · 102 m3 en dat is uit de ballon gestroomd.
22 a
28
volume in mL
1200
1000
800
600
400
200
0
27 a 5,8 cm
Bereken eerst de toename van het volume van het
kwik door de temperatuurstijging van 50 °C:
∆V = V0 ∆T
∆V = 182 · 10 −6 × 50 × 50 = 0,455 mm3
Dat extra volume zit in een “cilindertje” van kwik
met hoogte h en grondvlak π · r 2.
De straal van het grondvlak is de helft van de
binnendiameter: 0,05 mm.
π · r2h = 0,455 mm3
π · 0,052h = 0,455
h = 0,455/(π · 0,052) = 58 mm
Het streepje van de 50 °C staat 5,8 cm boven het
streepje van de 0 °C.
b Wanneer het glas uitzet wordt de binnendiameter
en het reservoir een klein stukje groter en het kwik
zal dus lager in de stijgbuis staan.
0
50
100 150 200 250 300 350
temperatuur in kelvin
b Het volume V en de temperatuur T zijn dan recht
evenredig: bij de helft van de temperatuur is ook
het volume gehalveerd (als je de druk constant laat).
54
242759_NAT 3E TF HAVO 4 UW_CH05.indd 54
853 °C
Bij temperatuurstijging zet het gat uit met dezelfde
uitzettingscoëfficiënt als het metaal. Je kunt dat als
volgt begrijpen. Zit er in een metalen plaat een gat
en zou door uitzetting de plaat twee keer langer en
twee keer breder geworden zijn, dan is ook het gat
twee keer breder geworden.
Voor het ijzer geldt:
∆L = L0 ∆T
invullen: 0,1 · 10 −2 = 12 · 10 −6 × 10 · 10 −2 × ∆T
∆T = 833 °C
Je begint bij 20 °C dus de eindtemperatuur is 833 +
20 = 853 °C.
© Noordhoff Uitgevers bv
15/07/13 12:34 PM
Hoofdstuk 5 Eigenschappen van stoffen
29
We gaan er van uit dat de schakelaar uitschakelt bij
hogere temperatuur. De binnenste laag is dan
gemaakt van staal en de buitenste van invar. Het
staal zet meer uit dan het strookje invar en trekt het
geheel steeds rechter. In het linker plaatje vormt het
staal een deel van de binnencirkel en het invar de
buitencirkel. Het staal in de binnencirkel moet dan
korter zijn dan het strookje invar in de buitencirkel.
Is het geheel helemaal recht dan zijn beide strookjes
namelijk even lang.
30 a Teken in figuur 5.15 een raaklijn bij T = 20 °C.
De raaklijn geeft de uitzetting weer die alleen klopt
bij een temperatuur van 20 °C met de uitzetting die
af te lezen is uit de originele kromme.
volume in m3
1,0140
1,0120
1,0100
1,0080
1,0060
1,0040
∆V
1,0020
1,0000
∆T
0,9980
0
b
c
d
e
10
20
30
40
50
temperatuur in °C
Neem voor ∆V = 1,0078 − 0,9980 = 0,0098 m3
∆T = 50 − 2 = 48 °C
Dat vul je in de formule in:
∆V = V0∆T
0,0098 = × 0,9980 × 48
met als resultaat:
= 0,0098/(0,9980 × 48) = 0,0002 = 0,2 · 10 −3
per °C.
Een negatieve uitzettingscoëfficiënt betekent dat
bij temperatuurstijging het volume kleiner wordt.
Water met een temperatuur van 4 °C heeft het
kleinste volume en dus de grootste dichtheid. Het
zakt naar de bodem van het meer. Op de bodem
van het meer zal de temperatuur 4 °C zijn. Boven in
is het water kouder, maar de dichtheid lager.
De kromme loopt in de buurt van de 40 °C steiler
dan rond de 20 °C. Het water zet rond de 40 °C dus
meer uit dan rond de 20 °C. De kubieke uitzettingscoëfficiënt is bij 40 °C groter dan bij 20 °C.
Je gebruikt weer de formule:
∆V = V0∆T
Neem een denkbeeldig kolom uit de oceaan met
een hoogte van 200 m en een doorsnede van 1 m2.
Die kolom heeft een volume V0 van 200 m3.
De temperatuurstijging ΔT is 1,0 °C.
Vul de gegevens in de formule in:
∆V = 1,2 · 10 −3 × 200 × 1 = 0,24 m3. Dat betekent dat
de kolom 24 cm hoger wordt. De zeespiegel stijgt
dan 24 cm.
© Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_CH05.indd 55
31
5.3 Stroming, geleiding en straling
De aarde verliest warmte door straling. Voor
stroming en geleiding is een tussenstof nodig en die
is er niet tussen de aarde en ruimte. Door geleiding
en stroming kan warmte niet verder dan de grenzen
van de dampkring.
32
pulsje
33
De wanden van de thermoskan houden de warmte
aan de ene kant en de kou aan de andere kant
gescheiden. Het maakt niet uit aan welke kant het
koud is of warm.
34
pulsje
35 a Je zoekt eerst de gegevens bij elkaar:
van glas is 0,93 W m −1K−1 (Binas)
oppervlak A van de ruit is 1,0 × 1,2 = 1,2 m2
dikte d van de ruit is 5 mm = 0,005 m
temperatuurverschil ΔT = 18 − 5 = 13 °C
Dit alles vul je in de formule in:
A ∆T
P = _____
d
P = 0,93 × 1,3 × 11/0,005 = 2902 J/s
Elke seconde stroomt er 2902 J door de ruit naar
buiten. In de hele winter stroomt er 2902 × 90 × 24
× 3600 = 2,26 · 1010 J.
b 1 kWh = 3600000 J
2,26 · 1010 J komt overeen met: 2,26 · 1010/3600000 =
6268 kWh.
c De kosten zijn: 6268 × 0,20 = 1254 euro. Dat is best
erg veel geld voor het warmteverlies door één ruit!
d Een temperatuurverschil van 0,5 °C is 26 keer kleiner
dan het temperatuurverschil van 11 °C.
het warmte verlies is daarmee ook 26 keer kleiner en
ook de kosten: 1254/22 = 48 euro.
36
Door ramen en de deuren verliest het huis de
meeste warmte en die zijn rood. Rood staat voor
warm en zwart (het dak) voor koud.
37 a 765 W
De grafiek geeft het uitgestraalde vermogen per m2
en bij een lichaamstemperatuur van 36 °C = 309 K
lees je af: 510 W. Het uitgestraalde vermogen voor
1,5 m2 is dan 1,5 × 510 = 765 W
b 510 W
De omgeving heeft een temperatuur van 5 °C = 278 K.
In de grafiek lees je dan weer het uitgestraalde
vermogen af en dat is 340 W. Het vermogen dat
1,5 m2 lichaamsoppervlak opvangt is
1,5 × 340 = 510 W. Hij verliest dus 765 – 510 = 255 W
38
pulsje
39
Antwoord D: P is evenredig met T 4.
Lees de grafiek af bij 150 K en 300 K de laatste
temperatuur is twee keer zo groot als de eerste.
Hoeveel keer groter is het vermogen?
Bij 150 K lees je af: 30 W en bij 300 K lees je af:
470 W. Hoeveel keer groter is 470 als je het
55
15/07/13 12:34 PM
Hoofdstuk 5 Eigenschappen van stoffen
vergelijkt met 30? Dat is 470/30 = 15,7 = 16 keer. Het
vermogen is dus evenredig met T4, want als T
verdubbelt dan verzestienvoudigt T4 (2 × 2 × 2 ×
2 = 16).
40 a Als de temperatuur niet meer stijgt zendt het asfalt
evenveel energie uit als dat het ontvangt. Het asfalt
zendt 650 W per m2 uit.
b 65 °C
De temperatuur die hoort bij een uitstraling van
650 W per m2 is volgens het diagram in figuur 5.24,
328 K = 55 °C.
41 a 52,0 W
Het elektrisch vermogen van het verwarmingselement is: P = UI.
Invullen levert op: P = 20,0 × 2,60 = 52,0 W.
b Ook 52,0 W. Alle warmte die bovenin ontstaat, moet
onderin afgevoerd worden anders zou het ergens
ophopen en daar zou de temperatuur stijgen.
c 3,80 · 102 W m −1 K−1
A ∆T
Gebruik de formule P = ______
d
De waarden die ingevuld moeten worden zijn:
P = 52 W
A = 9,15 · 10 −4 m2
∆T = 61,3 − 34,2 = 27,1 °C
d = 0,181 m
Dit levert op:
× 9,15 · 10 −4 × 27,1
52 = ________________ = 1,37 · 10 −1 ×
0,181
= 52/1,37 · 10 −1 = 3,80 · 102 W m −1 K−1
d Koper heeft 3,90 · 102 W m −1 K−1 (zie Binas tabel 8)
42 a 0,26 m2
De totale oppervlakte is: 0,20 × 0,30 (bovenkant) +
2 × 0,20 × 0,20 (twee zijkanten) + 2 × 0,30 × 0,20
(twee zijkanten) = 0,060 + 0,080 + 0,12 = 0,26 m2.
b De totale warmtestroom is 100 W en dat is gelijk
aan het vermogen (warmte en licht) dat de gloeilamp produceert.
c 0,018 W m −1 K−1
A ∆T
Gebruik de formule: P = ______
d
De eindtemperatuur in de doos gaat naar de 80 °C.
De temperatuur buiten de doos is 15 °C.
Invullen:
× 0,26 (80 − 15)
100 = ______________
0,003
= 100 × 0,003/(0,26 × 65) = 0,018 W m −1 K−1
d De isolatiewaarde van het karton is:
0,26 × 65/100 = 0,17 m2KW−1.
oppervlakte × temperatuurverschil
e warmtestroom = ______________________________
Rc
f De isolatiewaarde RC is hoog als het materiaal goed
isoleert en dat is beter dan de warmtegeleidingscoëfficiënt die juist laag is als het materiaal goed
isoleert. Een tweede voordeel is dat de dikte van het
materiaal al in de isolatiewaarde is verwerkt. Koop je
isolatiemateriaal dat twee keer dikker is dan is RC
ook twee keer groter.
56
242759_NAT 3E TF HAVO 4 UW_CH05.indd 56
43
44
Gebruik de formule:
A ∆T
P = ______
d
invullen : P = 0,014 × 1,0 × 90/0,01 = 126 W =
1,3 · 102 W.
5.4 Warmte uitwisseling
Een hoeveelheid water kan veel warmte opnemen
voordat de temperatuur 1 °C stijgt in vergelijking
met dezelfde hoeveelheid van een willekeurige
andere stof.
45 a 2,9 · 102 kg
Er bevindt zich 10 × 8,0 × 3,0 = 240 m3 lucht in het
lokaal. De massa van die lucht bedraagt
1,2 × 240 = 288 kg = 2,9 · 102 kg
b 3 · 101 W
De soortelijke warmte van lucht is
1,00 · 103 J · kg −1 · K−1
dus Qopgenomen = c · m · ∆T = 1,00 · 103 × 288 × 4 =
1,152 · 106 J
per leerling is dat 1,152 · 106 : 25 = 46080 J in
30 minuten = 1800 s
46080
dus het vermogen P = ______ = 25,6 = 3 · 101 W
1800
Een mens geeft minstens 100 W, dus er is veel warmte
door andere zaken opgenomen (muren, meubels).
46 a De massa van 1L water is 1 kg.
De warmtecapaciteit C is van het water in het bad is
dan:
C = Q/∆T = 80 × 4180/1 = 334400 = 3,3 · 105 J/K.
b De massa van de lucht is gelijk aan het volume van
de lucht maal de dichtheid van de lucht. De soortelijke warmte van lucht is 1000 Jkg −1K−1.
De warmtecapaciteit C is van de lucht in de badkamer is dan:
C = Q/∆T = 25 × 1,3 × 1000/1 = 32500 = 3,3 · 104 J/K.
c De warmte die het water heeft afgestaan is gelijk
aan de warmte de badkamer heeft opgenomen:
C∆T (badwater) = C∆T(badkamer)
334400 × 1 = 32500 × ∆T
334400
∆T = _______
32500 = 10 °C
Het juiste antwoord op de introvraag is antwoord C.
47
pulsje
48 a 0,28 °C
De soortelijke warmte van water is 4180 J·kg −1·K−1
en die van aluminium is 880 J·kg−1·K−1
dus de opgenomen warmte is:
Q = Qwater + Qaluminium = mw · cw · ∆T + mal · cal · ∆T =
(mw · cw + mal · cal) × ∆T
3,0 · 103 = (2,5 × 4180 + 0,200 × 880) × ∆T =
10626 × ∆T
30 . 103
∆T =_______ = 0,28 °C
10626
N.B.: Je mag bij 2 significante cijfers de massa van
2,5 L water gelijk stellen aan 2,5 kg.
© Noordhoff Uitgevers bv
15/07/13 12:34 PM
Hoofdstuk 5 Eigenschappen van stoffen
g
49 a De soortelijke warmte van melk is
3,9 · 103 J·kg −1·K−1
Voor de dichtheid van melk nemen we
1,03 · 103 kg/m3 = 1,03 kg/dm3 (zie Binas tabel 11), dus
10 mL = 0,01 L melk weegt 0,0103 kg
de temperatuurstijging is 72 °C
Qopgenomen = c · m · ∆T = 3,9 · 103 × 0,0103 × 72 = 2892
= 2,9 · 103 J
b 0,2 L
De warmte die de melk heeft opgenomen is
afgestaan door de koffie en het kopje; we nemen
aan dat de soortelijke warmte en de dichtheid van
koffie hetzelfde is als van water:
Qopgenomen = Qafgestaan = Qkoffie + Qkopje =
c · m · ∆T + C · ∆T
2892 = 4180 × m × 4 + 25 × 4 = 16720 × m + 100
2892 – 100 = 16720 × m
m = 2792/16720 = 0,167 kg
dat is 0,167 L = 0,2 L (één cijfer vanwege de temperatuurdaling van 4 °C)
50 a Omdat de warmte zich moet verplaatsen van
beneden naar boven en dat duurt een halve minuut.
b Het elektrisch vermogen P = UI = 5,0 × 3,6 = 18 W.
In 1 minuut is dat 60 × 18 = 1080 J.
c De temperatuurstijging is van 20,0 °C naar 29,5 °C in
4,5 minuut = 2,1 °C per minuut.
d De temperatuurdaling is van 30,8 °C (6,5 min) naar
29,5 (10 min). Dat is 1,3 °C in 3,5 min = 0,37 °C/min.
e Dan zou de temperatuurstijging groter zijn geweest,
namelijk 2,1 + 0,37 = 2,5 °C/min.
f De soortelijke warmte van aluminium is op de
volgende manier te berekenen (vul alles in voor een
tijdsduur van 1 minuut):
Qaluminium = mal cal ∆T
1080 = 0,500 × c × 2,5
c = 1080/(0,500 × 2,5) = 864 Jkg −1K−1
(de werkelijke waarde is 880 Jkg −1K−1)
© Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_CH05.indd 57
14
temperatuurverandering in °C
b 3,0 · 102 min = 5,0 h
de temperatuurstijging is nu 85 °C, dus
Q = 10626 × 85 = 9,03 · 105 J = 903 kJ
per minuut wordt 3,0 kJ toegevoerd, dus dat duurt
903 : 3,0 = 301 minuten = 5,0 uur
Je kunt het ook uitrekenen met een verhoudingstabel.
In werkelijkheid duurt het (veel) langer omdat de pan
bij hogere temperatuur (veel) warmte verliest door
straling en stroming en dus effectief minder warmte
opneemt.
Maar het vermogen is hier slechts 50 W; een gasfornuis heeft in werkelijkheid een veel hoger vermogen:
je brengt 2,5 L water in werkelijkheid in circa 7 min
aan de kook.
12
10
8
6
4
2
0
0
2
4
6
8
10
tijd in minuten
- In de eerste 0,5 minuut is er geen verandering
- het tweede deel loopt steiler want er gaat geen
warmte verloren.
- het derde deel loopt horizontaal omdat de
temperatuur constant blijft als er geen warmte
wordt aan gevoerd en er niets weglekt.
51
pulsje
52
-
53
De hoeveelheid water die hij verwarmt.
De begintemperatuur van het water.
De pan (de hoeveelheid metaal die hij verwarmt).
Het vermogen van de kookplaat (of de hoogte van
de gasvlam).
b De extra verwarmingstijd ∆t = t2 – t1 is nodig om het
ei ∆T graden in temperatuur te laten stijgen (∆T =
100 – Tbegin)
Dus voor de extra toegevoerde warmte geldt:
Q = P · ∆t, maar ook Q = Cei · ∆T
(let op het verschil tussen ∆t (de extra tijd) en ∆T
(de temperatuurstijging))
Hij kan dus Cei berekenen met de formule
P · ∆t = Cei · ∆T
Daarvoor moeten bekend zijn:
- het vermogen P,
- de begintemperatuur Tbegin,
- de opwarmtijden t1 en t2
c De warmteverliezen beperken door:
- kleiner temperatuurtraject,
- temperatuurtraject deels onder en deels boven
kamertemperatuur,
- uitstraling en verdamping beperken.
Dezelfde proef doen met méér eieren tegelijk, dan is
het tijdverschil groter en dus nauwkeuriger te
meten.
Zie model 5.53
5.5 Eigenschappen van gassen
54 a Als het volume verdubbelt, moet de druk halveren.
Neem de volumes 5,0 en 10 cm3. De druk zou dan
van 190 kPa moeten halveren tot 95 kPa en dat is
volgens de tabel niet het geval. De druk bij 10 cm3 is
geen 95 maar 101 kPa.
b De volume V en druk p het zijn omgekeerd evenredig. Dat betekent dat V evenredig is met 1/p. Maak
een grafiek van V uitgezet tegen 1/p. Dat moet een
rechte lijn opleveren door (0,0) als aan de wet van
Boyle is voldaan.
57
15/07/13 12:34 PM
Hoofdstuk 5 Eigenschappen van stoffen
V in cm3
p in kPa
10
9,0
8,0
7,0
6,0
5,0
4,0
101
110
125
140
160
190
235
1/p in 10 −3
kPa −1
9,9
9,1
8,0
7,1
6,3
5,3
4,3
58
p1V1
____
T1
p2 = 4670
Gebruik je deze vorm van de algemene gaswet dan
hoef je voor druk en volume niet de standaard
eenheden te gebruiken omdat je die eenheid zowel
links als rechts in de vergelijking gebruikt. Voor de
temperatuur moet je wel altijd kelvin gebruiken.
1/p in 1/kPa
0,01200
0,01000
59
0,00600
0,00400
0,00200
0,00000
0
2
4
6
8
10 12
V in cm3
De grafiek gaat niet door (0,0) dus dit gas gedraagt
zich niet volgens de wet van Boyle.
55
Eerst de gegevens in een overzichtelijke tabel:
100 °C
0 °C
50,0 kPa
36,6 kPa
We zoeken de temperatuur waarbij de druk 0 kPa is.
Daalt de druk 13,4 kPa dan hoort daar een temperatuurdaling bij van 100 °C. Bij een drukdaling van
1 kPa hoort dan een temperatuurdaling van
100/13,4 = 7,46 °C. De druk moet nog 36,6 kPa
dalen en daar is dan een temperatuurdaling voor
nodig van 7,46 × 36,6 = 273 °C.
Volgens de gegevens is het absolute nulpunt 273 °C
onder 0 °C = −273 °C.
56
T
)
A, C, E/F, D, B ( p is evenredig met __
V
57 a 5 m3
p ·V
p1 · V1 _____
1,0 x 1,8 0,3 x V2
______
→
= 2 2 → ________ = _______
T2
T1
273 + 18 273 − 50
p × 50
p2V2 _________
180 × 400 ______
= 2973 →
= ____
→
300
T2
De einddruk is 4,7 · 103 kPa
Zet de meetpunten in Excel en laat de trendlijn
tekenen. Dit geeft het diagram dat hieronder is
getekend:
0,00800
4,7 · 103 kPa
De begintemperatuur is 27 °C = 273 + 27 = 300 K.
De eindtemperatuur is 700 °C = 700 + 273 = 973 K.
Gebruik de algemene gaswet in deze vorm:
pV
Gebruik de algemene gaswet: ___ = nR
T
Schrijf die wet in deze vorm:
nRT en vul de gegevens in:
V = ____
p
1 × 8,31 × 273
___________
V=
= 2,24 · 10 −2
1,0 · 105
Het molaire volume is inderdaad 2,24 · 10 −2 m3.
Deze waarde vind je ook in Binas tabel nr. 7.
60 a Bereken eerst de druk als er geen volumeverandering zou zijn:
T in K
p in bar
58
242759_NAT 3E TF HAVO 4 UW_CH05.indd 58
315
5,27
dan vind je 5,27 bar.
De werkelijke druk is iets lager, dat kan alleen als het
volume ook iets groter is geworden.
b 1,4 L
p ·V
p1 · V1 _____
5,1 × V2
4,8 × 1,4 _______
_____
= 2 2 → ________
273 + 14 = 273+42 →
T1
T2
V2 = 1,446 = 1,4 L
61 a 113 bar
Gebruik de drukwet van Gay Lussac.
p2
p
p1 ___
200 = ___
___
= 2 → ____
273 154 → p2 = 113
T1
T2
De druk is dan 113 bar.
b De druk neemt volgens Gay Lussac lineair af (1)
totdat er condensatie optreedt. Dan neemt de druk
snel af, ongeveer volgens (2)
V2 = 4,60 = 5 m3
zuurstoffles
250
p in bar
b Eerst bij gelijkblijvend volume de nieuwe druk
berekenen:
p2
p
p1 __
1,0 ___
__
= 2 → ___
291 = 223 → p2 = 0,766
T1 T2
Vervolgens bij constante T het nieuwe volume
berekenen:
p1 · V1 = p2 · V2 → 0,766 × 1,8 = 0,3 × V2
V2 = 4,60 = 5 m3
Je kunt ook eerst de volumewet en dan de wet van
Gay-Lussac gebruiken.
287
4,8
alleen
gas (1)
200
150
100
(2) damp
plus vloeistof
50
0
0
100
200
T in K
300
© Noordhoff Uitgevers bv
15/07/13 12:34 PM
Hoofdstuk 5 Eigenschappen van stoffen
62 a 2,15 · 105 m3
In de turbine stroomt per uur 56 · 103 m3 gas (V1) met
een druk van 40 bar (p1) en een temperatuur van
95 + 273 K (T1). Uit de turbine komt per uur een
onbekende hoeveelheid V2 met een druk van 8,0 bar
(p2) en een temperatuur van 8,0 + 273 K (T2).
Gebruik de algemene gaswet in deze vorm:
p V
p1 V1 ____
8 × V2
40 × 56 · 103
____
= 2 2 →___________ = _______
→
T1
T2
8 + 273
(93 + 273)
8 × V2
2,24 · 106 ______
________
=
→ V2 = 215 · 105
366
281
Het volume dat per uur uit de turbine komt is
daarmee: 2,15 · 105 m3.
b 44 kg/s
Dit ga je uitrekenen met de formule:
Q = mc ΔT
voor het water:
6,4 · 106 = m × 4180 × 35
m = 6,4 · 106/(4180 × 35) = 44 kg/s.
c 1,4 · 102 Jkg −1K−1
De soortelijke warmte van het aardgas bereken je
met de formule:
Q = mcΔT
De massa van het gas moet je nog uitrekenen.
1 m3 aardgas heeft een massa van 0,833 kg bij een
druk van 1 bar (dichtheid: zie Binas). Wordt de druk
40 bar dan wordt de dichtheid ook 40 maal groter,
er van uitgaande dat het een ideaal gas is (en blijft).
De dichtheid is dan 33,3 kg/m3. Je rekent het uit per
seconde: de gasstroom is 56 · 103 m3 per uur. Per s
wordt dat: 56 · 103/3600 = 15,6 m3.
Vul de formule in:
6,4 · 106 = 15,6 × 33,3 × c × (95-8)
6,4 · 106 = 4,52 · 104 × c
c = 6,4 · 106/4,52 · 104 = 1,4 · 102 Jkg −1K−1
d De stroomsterkte bereken je met: P = UI
4,0 · 106 = 10 000 × I → I = 4,0 · 106/10 000 =
4,0 · 102 A.
63
64
De molaire massa van butaan is 1,32 keer zo groot
als van propaan, dus 1 m3 butaan is ook 1,32 keer zo
zwaar als 1 m3 propaan (want 1 m3 bevat evenveel
mol)
Butaan levert 1,29 keer zoveel energie per m3 als
propaan, dus per kilo (of per gram) is dat vrijwel
hetzelfde.
Enkelvoudige koolwaterstoffen leveren bij verbranding allemaal ongeveer evenveel energie per
C-atoom; en de molaire massa wordt grotendeels
bepaald door het aantal C-atomen.
34 °C
Het beginvolume van de lucht is 0,510 L.
Na verwarmen komt daar een extra volume bij met
een lengte van 32 cm en een cirkeloppervlakte van
π × 0,52 = 0,785 cm2.
Extra volume is 32 cm × 0,785 cm2 = 25,1 cm3.
1 L = 1000 cm3.
Het eindvolume van de lucht is dan 0,510 + 0,0251 =
0,535 L.
© Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_CH05.indd 59
deze gegevens vullen we in:
V
0,535
0,510
_____
= __2 → ________
273 + 20 = T2
T1 T2
0,510 × T2 = (273+20) × 0,535
T2 = 293 × 0,535/0,510
T2 = 293 × 1,049 = 307 K = 34 °C.
V1
___
65 a Het deksel zit op de pot geschroefd. Pas bij een
kleine overdruk wordt hij omhoog gedrukt en kan er
lucht en waterdamp ontsnappen.
b 0,86 bar
p
p2
p1 __
1,1 ____
___
= 2 → ___
373 = 293 → p2 = 0,864 = 0,86 bar
T1 T2
c De wet geldt niet omdat het aantal dampmoleculen niet constant is. Dit aantal neemt door
condensatie af.
Een damp gedraagt zich dus niet als een ideaal gas als
er ook vloeistof aanwezig is, tenzij je er
rekening mee houdt dat het aantal deeltjes in het gas
niet constant is. Als je dat op de juiste manier in
rekening brengt kun je gewoon de algemene gaswet
gebruiken.
d 0,023 bar
Het aantal mol n = 0,86 · 10 −3 : 18 = 4,78 · 10 −5 mol
p·V
____
n·R·T=
= n · R ⇒ p = _______
T
V
4,78
· 10 −5 × 8,3145 × 293
____________________
= 2328 Pa = 0,023 bar
50 · 10 −6
De druk is dus: 0,023 bar.
Let er op dat je bij het gebruik van de algemene
gaswet op deze manier altijd de SI-basiseenheden
moet gebruiken.
5.6 Optische eigenschappen van stoffen
66 a 2 Vergelijk met de tekening van figuur 5.44.
b 4 Vergelijk weer met de tekening van figuur 5.44.
c De invalshoek is 44º, de brekingshoek 14º.
Je moet hoek 2 en 4 opmeten. Verleng de lijntjes
totdat je je geodriehoek goed kunt aflezen. Je mag
niet meer dan 1º afwijken.
d 44º Even groot als hoek 2 omdat je weet dat i = t.
67 a Gegeven: i = 30º en n = 1,5 (opzoeken in Binas)
sin30°
sini = n ⇒ ______
____
= 1,5 ⇒
sinr
sinr
0,5
___
sinr = 1,5 = 0,333
r = sin −1(0,333) = 20˚
b Als de straal een hoek van 40° met het perspex
maakt, dan is de invalshoek 90° – 40° = 50°.
Gegeven: i = 50° en n = 1,5.
sin50°
sini = n ⇒ ______
____
= 1,5 ⇒
sinr
sinr
0,766
sinr = ______
1,5 = 0,5107 ⇒
−1
r = sin (0,5107) = 30,7° = 31°
59
15/07/13 12:34 PM
Hoofdstuk 5 Eigenschappen van stoffen
68
Uit figuur 5.44 haal je de gegevens: i = 44º en
r = 14º.
sin44° ______
0,695
sini = ______
= 2,9
=
n = ____
sinr
sin14° 0,242
Let er op dat je je rekenmachine in de mode graden
(“degree”) hebt staan.
71
69 a De brekingsindex van perspex is 1,5. De grenshoek is
dan:
1
sin g = ___
1,5 = 0,67
g = 42º
b Diamant heeft de grootste brekingsindex en dus de
kleinste grenshoek: n = 2,4 en g = 24º.
De glazen bol
a n = 1,51
b De hoek van inval is 45°
c Er geldt:
sin 45°
sin i → sin r = ______
sin i = 151 → sin r = ____
____
1,51
1,51
sin r
0,707
=
0,468
sin r = _____
1,51
r = sin −1(0,468) = 27,9 = 28°
d
45°
28°
28°
70 a Driehoekig prisma (tophoek 45º), eerste vlak:
i = 0º ⇒ r = 0º. De straal gaat dus rechtdoor.
Bij het tweede vlak i opmeten (eerst de normaal
tekenen !): i = 45º.
Nu r berekenen:
sin45°
sini = __1 ⇒ ______
____
= 0,6098 ⇒
sinr
sinr n
0,7071
sinr = _______ = 1,16
0,6098
r = sin −1(1,16): ERROR
Er is dus totale terugkaatsing.
Bij het derde vlak geldt weer i = 0º en dus r = 0º.
Tekening:
F
e Die hoek van inval moet ook weer 28° zijn want de
driehoek met de tweemaal 28° is gelijkbenig.
f De hoek van breking is dan ook weer 45°.
met een berekening:
sin 28° = ___
sin i = __1 → ______
____
1
1,51 = 0,662
sin r
sin r n
sin 28° = 0,709
sin r = ______
0,662
g
h
i
j
b Vierzijdig prisma (scherpe hoek 70º), eerste vlak:
i = 20º en n = 1,64.
sin20° = 1,64 ⇒
sini = n ⇒ ______
____
sinr
sinr
0,3420
_______
= 0,2085
sinr=
1,64
r = sin −1(0,2085) = 12,0°
De straal breekt naar de normaal toe en treft daarna
het rechter schuine vlak. Daar geldt:
i = 12º en n = 1,64.
sin12° = 0,6098 ⇒
sini = __1 ⇒ ______
____
sinr
sinr n
0,2079
_______
= 0,3410
sinr =
0,6098
r = sin −1(0,3410) = 19,9°
(Waarom vind je niet exact 20º ?)
k
242759_NAT 3E TF HAVO 4 UW_CH05.indd 60
r = sin −1(0,709) = 45°
Zie tekening hierboven.
Zie tekening hierboven.
Zie tekening hierboven.
De straal van de bol is 10 cm. Meet de afstand van
het middelpunt van de bol tot aan het brandpunt F
en reken dat om de werkelijke afstand en je vindt
iets in de buurt van de 12 cm.
Ja dat klopt wel ongeveer.
Toepassing
Opgave 1 Thermometers
1
8,8 J
De hoeveelheid warmte die het kwik in de thermometer per graad temperatuurstijging opneemt, is te
berekenen met de volgende formule:
Qkwik = mkwikckwik∆T = 4,8 · 10 −3 × 0,138 · 103 × 1 =
0,662 J.
De hoeveelheid warmte die het glas van de thermometer per graad temperatuurstijging opneemt,
bereken je op dezelfde manier:
Qglas = mglascglasΔT = 10,2 · 10 −3 × 800 × 1 = 8,16 J.
Dus de hoeveelheid warmte die de thermometer per
graad temperatuurstijging opneemt is
Qkwik + Qglas = 0,662 + 8,16 = 8,8 J.
2
60
45°
Bij temperatuurstijging gaan de kwikmoleculen
sneller bewegen. Ze botsen daardoor vaker en
harder tegen elkaar met als gevolg dat de gemiddelde afstand tussen de moleculen toeneemt en het
kwik dus uitzet.
© Noordhoff Uitgevers bv
15/07/13 12:34 PM
Hoofdstuk 5 Eigenschappen van stoffen
3
8,3 J/°C.
De temperatuur van het water daalt met
ΔTw = 17,2 − 15,5 = 1,7 °C. Het water staat hierbij
warmte af:
Qaf = mwatercwater ΔTw = 18 · 10 −3 × 4,18 · 103 × 1,7 = 128 J.
Deze warmte wordt opgenomen door de thermometer die daardoor 15,5 − 0 = 15,5 °C in temperatuur
stijgt.
De warmtecapaciteit van de thermometer is dus
C = Q/∆T = 128/15,5 = 8,3 J/°C.
Gebruik de eerste 10 seconde van de raaklijn om de
richtingscoëfficiënt te bepalen. De richtingscoëfficiënt van de raaklijn is:
(28,8 − 21,3)/10 = 0,75 °C/s.
Een afwijking van 10% is nog correct.
9
0,17 W/°C
P = k(Twater − Tkwik )
Kijk weer naar tijdstip t = 5 s. De temperatuur stijgt
daar 0,75 °C per s.
Om het kwik 0,75 °C (per seconde) in temperatuur te
laten stijgen is nodig aan warmte: Q = mc∆T =
0,0061 × 140 × 0,75 = 0,64 J.
Vervolgens vul je de formule in:
0,64 = k × (28,8 − 25,1)
0,64 = k × (3,7)
k = 0,64/3,7 = 0,17 W/°C
De eenheid van k is de eenheid van vermogen (W)
gedeeld door de eenheid van temperatuur( K of °C)
10
- De dikte van de glazen wand van het reservoir.
- De glassoort van het reservoir
Opgave 2 De kwikthermometer
4
Je hebt de dichtheid van kwik nodig, Binas:
13,5 kg/m3 = 13,5 g/cm3. Er geldt: dichtheid = massa/
volume en dus volume = massa/dichtheid = 6,1 g/13,5
g/cm3 = 0,45 cm3.
5
8,2 · 10 −5 cm3
Er geldt: ΔV = V0 ΔT
Dat ga je invullen:
ΔV = 182 · 10 −6 × 0,45 × 1,0 = 8,2 · 10 −5
De volume toename per graad is 8,2·10 −5 cm3.
(In Binas staat voor de metalen de lineaire uitzettingscoëfficiënt vermeld, maar omdat kwik een
vloeistof is staat bij kwik de kubieke uitzettingscoëfficiënt.)
6
1,0 · 10 −4 cm2
Je rekent eerst de toename van het volume van het
glasreservoir om naar cm3. 1,1 · 10 −11 m3 =
1,1 · 10 −11 × 1 000 000 = 1,1 · 10 −5 cm3.
Het kwik dat door die ene graad stijging omhoog
gaat in de stijgbuis is het extra volume van het kwik
min het extra volume van het uitzettende reservoir:
8,2 · 10 −5 − 1,1 · 10 −5 = 7,1 · 10 −5 cm3. De stijging van het
kwik in de stijgbuis is voor 1,0 °C:
27,9/40 = 0,70 cm
Dat volume in de stijgbuis is een cilindertje met
hoogte 0,70 cm en cirkeloppervlakte gelijk aan de
doorsnede van de stijgbuis.
Doorsnede × 0,70 cm = 7,1 · 10 −5 cm3
Doorsnede = 7,1 · 10 −5/0,70 = 1,0 · 10 −4 cm2
Omdat de temperatuurstijging per seconde steeds
kleiner wordt: de grafiek gaat steeds vlakker lopen.
8
0,75 °C/s.
Teken in de grafiek de raaklijn bij t = 5 s. De steilheid
van deze raaklijn is gelijk aan de temperatuurstijging per seconde op het tijdstip t =5 s.
temperatuur in °C
7
30
29
28
27
26
25
24
23
22
21
20
19
0
5
© Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_CH05.indd 61
10
Opgave 3 Dubbel glas
11
De formule kan omgeschreven worden tot:
P . Δs
= ______
A · ΔT
W = W · m−1 · K−1
W · m = _____
De eenheid is dus ______
m2 · K m · K
12
6,2 kJ/s
= 0,93 W/m·K (Binas tabel 10), dus
20
ΔT = 0,93 × 1,00 × _______
P = · A · ___
0,0030 = 6200
Δs
Per seconde wordt 6,2 · 103 J door deze ruit geleidt.
13
310 W/m2 · K
6200 = 310
P = ________
U = ______
A · ΔT 1,00 × 20
De U-waarde van de ruit is 310 W/m2 · K
14
Door de twee formules voor P te vergelijken vind je:
U = ___
Δs
ook hiermee kun je U uitrekenen:
0.93
= 310 Wm −2K−1
U = ___ = _______
Δs 0,0030
15
tijd in s
61
15/07/13 12:34 PM
Hoofdstuk 5 Eigenschappen van stoffen
15
De warmtegeleidingscoëfficiënt van lucht staat in
Binas: lucht = 24 · 10 −3 W/m·K
Door elke glasplaat én door de luchtlaag moet hetzelfde vermogen gaan (het is een soort ‘serieschakeling’).
Door het glas:
0,5
ΔT = 0,93 × 1,00 × _______
P = · A · ___
0,0030 = 155 W
Δs
en door de luchtlaag:
19
ΔT = 0,024 × 1,00 × _______
P = · A · ___
0,0030 = 152
Δs
Dat klopt dus. Het vermogen is vrijwel gelijk.
Je kunt ook redeneren: van de lucht is 39 keer zo
klein als van glas, dan moet er bij hetzelfde vermogen
een 39 keer zo groot temperatuurverschil over staan.
16
Zie vorige vraag.
17
7,7 Wm −2·K−1
neem voor het vermogen 154 W:
154
P = ________
= 7,7
U = _____
A · ΔT 1,00 × 20
23
p2V2
p1V1T2
= ____
⇒ p2 = _____
T1
T 2
T1V2
5
×
1,0
×
355
1,00
.
10
= _________________ = 1,1 · 105 Pa
287 × 1,12
p1V1
____
Opgave 5 Heteluchtballon
V1 __
V
= T 2, ombouwen:
24 We gebruiken de gaswet: __
T1
2
T
V2 = V1 × __2
T2
Invullen:
273 + 56
3
V2 = 490 × ________
273 + 20 = 550 m
25
4,3 minuut
Gebruik Q = mc∆T
Invullen: Q = 6,0 · 102 × 1,0 · 103 × (56 – 20) = 21,6 · 106 J.
De stookwaarde van propaangas is 93,8 · 106 J/m3
(Binas).
Het gas levert per minuut 53 · 10 –3 × 93,8 · 106 =
4,97 · 106 J.
De tijd wordt dan: 21,6 · 106/4,97 · 106 = 4,3 minuut.
26
Als de branders aan staan, stijgt de luchtdruk in de
ballon en die luchtdruk wordt groter dan de luchtdruk buiten de ballon. Er stroomt dus lucht uit de
ballon en de massa van de lucht in de ballon wordt
kleiner als de branders aan staan.
De U-waarde is 7,7 Wm–2 · K–1
18
Dan zou er een veel groter getal uitkomen, want de
U-waarde van één zo’n glasplaat is al 310 W/m2 · K
19
De U-waarde van de glasplaten is al berekend, die
0,024
–2 –1
= ______
van het luchtlaagje is __
0,0030 = 8,0 Wm K
Δs
1 + ___
1 = 0,13
1 = ___
1 + ___
dus: _____
Utotaal 310 8,0 310
dus Utotaal = 1/0,13 = 7,6 Wm–2 · K–1
20
Er komt dan 5,9 W/m2 · K uit.
We gaan even uit van de bovengenoemde glasplaat
van 3 mm dikte, met een U-waarde van 310 W/m2 · K
De U-waarde van 2 mm lucht berekenen we als bij
0,024
= 12 Wm–2 K–1
vraag i: ___ = _______
Δs 0,0020
en de totale U-waarde met de formule van vraag 19:
_____
1
Utotaal
1,1 · 105 Pa
Als de fles in het hete water staat is het volume van
de afgesloten lucht:
V2 = Vfles + Vballon = 1,0 + 0,12 = 1,12 L.
De temperaturen in kelvin zijn:
T1 = 14 + 273 = 287 K en T2 = 82 + 273 = 355 K.
De luchtdruk in de fles bij 82 °C wordt dan berekend
met:
Opgave 6 De spiegel in het aquarium
27 Omdat de lichtstraal daar loodrecht invalt.
28
42°
Je start met de hoek van 60°. Hoek EDB en hoek DBA
zijn Z-hoeken. Daaruit volgt dat hoek DBA ook 60° is.
Daaruit volgt dat hoek ABF 30° is.
__
1 __
1
1
= ___
310 + 12 + 12 = 0,17
dus Utotaal = 5,9 W/m2 · K
lucht
3 · 10 J
De temperatuurstijging van de fles is:
∆T = 82 – 14 = 68 °C.
De soortelijke warmte van glas is:
c = 8 · 102 Jkg–1K–1.
De benodigde warmte is dus:
Q = cm∆T = 800 × 0,600 × 68 = 3 · 104 J
i
F
A
242759_NAT 3E TF HAVO 4 UW_CH05.indd 62
G
B
4
62
r
water
Opgave 4 Ballon op de fles
21
De massa van de lucht is veel kleiner dan die van het
glas, terwijl de soortelijke warmte niet zoveel
verschillen. De benodigde warmte voor de temperatuurstijging van de lucht zal dan verwaarloosbaa
zijn ten opzichte van de benodig de warmte voor de
temperatuurstijging van het glas.
22
C
60°
E
D
© Noordhoff Uitgevers bv
15/07/13 12:34 PM
Hoofdstuk 5 Eigenschappen van stoffen
Volgens de spiegelwet is dan ook hoek FBC 30°.
Hoek ABC is dan 60° en hoek BCF 30° want driehoek
BCG is een rechthoekige driehoek.
Conclusie: de hoek van inval i bij punt C is 30°.
De brekingsindex van water is 1,33.
Wet van Snellius:
sin i = __1
____
sin r n
sin 30
1
Invullen: ______ = ____
1,33 → sin r = 1,33 × sin 30
sin r
sin r = 0,665 → r = sin–1 (0,665) → r = 42°
1
Proefwerkopgaven
0,81 m
Je rekent eerst uit hoeveel langer de koperen leiding
wordt door de temperatuurstijging van 20 °C:
∆L = L0 ∆T = 16,8 · 10 −6 × 800 × 20 = 0,27 m.
De straal van het grote wiel is 3 maal groter dan dat
van het kleine wiel. Het contragewicht gaat daarom
3 × 0,27 = 0,81 m omlaag.
2 a 16 °C
b Een raaklijn aan het begin van de grafiek geeft de
temperatuurstijging zonder warmteverlies, want in
het begin is er nog geen warmteverlies omdat er
nog geen temperatuurverschil is met de omgeving.
De gestreepte raaklijn hieronder heeft een helling
− 16
______
van 80
2,5 = 25,6 °C/min
Dus zonder verlies wordt er per minuut opgenomen:
Qopgenomen = Qwater + Qkopje = c · m · ∆T + C · ∆T =
(c · m + C) · ∆T = (4180 × 0,050 + 31) × 25,6 = 240 ×
25,6 = 6144 J
per seconde is dat 6144 : 60 = 102 J
dus het opgenomen vermogen is 102 W = 1,0 · 102 W
3 a Voordeel: Je perst per slag meer lucht in de band.
(Je hoeft dus minder slagen te maken).
Nadeel: Om dezelfde druk op te bouwen is bij een
groter zuigeroppervlak (A) een grotere kracht nodig,
want: F = p · A.
(Je moet dus een grotere kracht uitoefenen bij een
bredere buis).
b 6,4 bar
Als de straal van de buis 1,7 cm aan de binnenkant is:
A = π · 1,72 = 9,08 cm2 = 9,08 · 10 –4 m2
F m · g 50 · 9,81
p = __z = _____ = ________−4 = 5,4 · 105 Pa =
A
A
9,08 · 10
5,4 bar is de overdruk.
c Temperatuurstijging heeft geen invloed op de druk,
want de druk hangt alleen af van de kracht en de
oppervlakte.
(T heeft wel invloed op het volume, want:
p·V
____
n · R · T T omhoog dus
= n · R ⇒ V = _______
p
T
V omhoog, het volume zal dus wel toenemen).
4
T in °C
100
80
60
40
20
0
0
5
10
15
20
25
t in min
Vergeet niet om de tijd naar s om te rekenen!
c 74 W
Door een raaklijn te tekenen bij T = 40 °C kunnen we
het netto opgenomen vermogen en het uitgestraalde vermogen bij die temperatuur bepalen.
Zie de raaklijn:
100 − 28 = 7,2 °C/min
de helling is ________
10
dus per minuut neemt het kopje (met water) nu op:
Q = 240 × 7,2 = 1728 J
toegevoerd wordt nog steeds 6144 J (zie vraag b);
uitgestraald wordt dus 6144 – 1728 = 4416 J per
minuut:
Puitgestraald = 4416 : 60 = 73,6 J/s = 74 W
© Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_CH05.indd 63
De streep-stippellijnen zijn de normalen. Omdat de
breking van glas (of kunststof) naar lucht plaatsvindt,
moet de brekingshoek groter zijn dan de invalshoek.
Je kunt voor een goede lichtbundel beter bolle LEDs
gebruiken.
Bij de bolle LED zijn de gebroken stralen minder sterk
divergent dan bij de platte LED. De lichtintensiteit op
afstand is bij bolle LEDs dus groter dan bij platte LEDs.
63
15/07/13 12:35 PM
Hoofdstuk 6 Kracht als vector
Hoofdstuk 6
Kracht als vector
1
2
Introductie
Alleen bij de sport speed skydiving (vrije val met het
hoofd naar beneden) worden hogere snelheden
bereikt. Het wereldrecord is daar boven de
502 km/h. (Bron: Wikipedia op 20-2-2013)
8
De grootste weerstandskracht is de luchtweerstand,
maar er is ook wrijving van de ski’s op de sneeuw.
9
De skieër versnelt nog steeds → Fw < FII
Fw < F⁄⁄
90 km/h staat gelijk aan 25 m/s. De beginsnelheid is
0 m/s dus Δv = 25 m/s
Invullen in formule voor a:
Fz
25
Δv = ___
= 8,3 ms2
agem = ___
Δt 3
α
3
De luchtweerstand wordt steeds groter.
4
Veronderstel een constante snelheid, van
251,400 km/h in de timingszone. (Dat staat niet in
de opgave.) Omgerekend is dat 69,833 m/s.
10
Tijdstap: 0,001 s; stoppen op 15 sec
Begin bijvoorbeeld alfa = 37 gr (0,65 Pi)
afremzone
12,5–25 s
tijdsinterval
0–11 s
11–12,5
plaats
0–450 m
450–550 m 550–1000 m
x in m
1000 m
versnelling (m/s2)
snelheid
snelheit (m/s)
alfa (rad)
Fres (N)
Fz sin(alfa) - Fw,l - Fw,s luchtweerstand (N)
schuifweerstand
schufweerstand (N)
(N)
massa (kg)
0,12 vˆ2
0,050*Fz*Cos(alfa)
m = 85 kg
g (m/s2)
zwaartekracht (N)
Oplosser: Euler
450
hoogte in ...
timingszone
hoogte (m)
Fwl en Fwr kunnen verbeterd worden.
Aannames bij het maken van de schets:
De ‘plaats’ gemeten langs de helling.
Belangrijke punten op de x-as: 11 s voor de versnelling (ondergrens aangehouden); 1,5 s voor de timing
(afgeronde waarde), en voor de afremzone:
450 m/35 m/s = 12,9 s
versnellingszone
Model van de beweging.
Gemaakte keuze: De hoogte begint bij 450 m en neemt dan af.
Er kan dus best een negatieve waarde uitkomen (Dat is dan lager dan de finisch)
100,000
t = _vs_ = ________ = 1,432 s
69,833
5
Tan α = 0,51
F⁄⁄
400
350
300
250
200
150
100
550 m
450 m
50
0
0
0
6
7
5
11 12,5
t in s
25
Of, simpeler: a = g · sin 37° = 5,9 m/s2
64
242759_NAT 3E TF HAVO 4 UW_CH06.indd 64
4
6
8
10
12
14
16
t in s
Varieer met de parameters voor f en voor de luchtweerstand om een realistische grafiek te krijgen. De
hoek is in het getoonde model nog constant.
Het plaatje van het parcours is sterk overdreven. De
hellingshoek is in werkelijkheid 37°
FII = Fz · sin 37° = 9,8 · 85 · 0,602 = 5,0 · 102 N
FII ________
5,02 · 102
FII = m · a ⇒ a = __
= 5,9 m/s2
m=
85
2
1
6.1 Krachten zijn vectoren
temperatuur → scalar
wind”kracht” → vector
snelheid → vector
luchtdruk → scalar
neerslag → scalar
© Noordhoff Uitgevers bv
15/07/13 12:35 PM
Hoofdstuk 6 Kracht als vector
c De luchtweerstand neemt eerst toe omdat de raket
steeds sneller gaat; maar op grotere hoogte neemt
hij weer af omdat de lucht steeds ijler wordt.
Bij de vectoren is niet alleen de grootte, maar ook de
richting van belang.
2 a
750 N
750 N
^ 300 N
b 1 cm =
c Deze kracht is even groot als de trekkracht.
750 N
6 a 6,4 · 102 N
Fn = Fz = m · g
⇒ Fn = 65 × 9,81 = 637 = 6,4 · 102 N
b Even groot, want nog steeds is Fn = Fz.
c B
Op het onderste punt is de plank het meest
vervormd.
7
Pulsje
8 a
Ftrek
750 N
FN
d 2,5 cm
3 a Ja. De snelheid is constant, dus er is geen
nettokracht.
b De luchtweerstand is kennelijk 195 N.
Fnetto = 0 → Fmotor = Frolweerstand + Fluchtweerstand
c
Fz
195 N
Fw
240 N
1 cm ^= 120 N
1 Ftrek door het touw op de man naar voren
2 Fw door de grond op de man naar achteren
3 Fz door de aarde op de man omlaag
4 Fn door de grond op de man omhoog
b C is juist. (nog beter: na de laatste man).
Het touw staat daar strak door alleen de trekkracht
van de laatste man.
A is onjuist. Alleen in het touw tussen de voorste
man van beide teams is de kracht overal hetzelfde.
B is onjuist. Daar staat het touw strak door samenwerkende trekkrachten van 7 van de 8 teamleden.
Tussen beide teams is de spankracht dus nog groter.
45 N
4 a 816 m
De kabel breekt wanneer het gewicht van de kabel
20 kN bedraagt. Gewicht van 1 m kabel:
Fz = m · g = 2,50 · 9,8 = 24,5 N
b
Fmax
20 · 103 = 8,2 · 102 m
Maximale lengte: _______
= _______
24,5
Fper meter
spankracht
vector
lengte
scalar
massa
scalar
5 a 3,0 · 106 N
Fnetto = Fstuw – Fz
⇒ 5,0 · 10 –5 = Fstuw – 2,50 · 10 –6
⇒ Fstuw = 0,50 · 10 –6 + 2,50 · 10 –6 = 3,0 · 10 –6 N
b Fnetto neemt toe doordat:
- de massa van de raket kleiner wordt: de brandstof
wordt verbruikt;
- de gravitatieversnelling kleiner wordt op grotere
afstand van de aarde.
Lastig: De luchtweerstand speelt natuurlijk wel een
rol bij grote snelheid; maar wanneer de raket
opstijgt en versnelt neemt de dichtheid van de lucht
sterk af.
© Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_CH06.indd 65
9
11
Weer in M. Voor het verplaatsen maakt het niet uit
wie van beiden er trekt. Beiden hebben even veel
weerstand op het ijs blijkt uit de tekst. De kracht
van Nora op Jens is altijd even groot als omgekeerd.
6.2 Krachten onder een hoek
De diagonaal is 3,0 cm
Fsom = 7,5·102 N
65
15/07/13 12:35 PM
Hoofdstuk 6 Kracht als vector
12 a
18
60°
20°
somkracht: F1 + F2
Let op:
100° !
somkracht: F1 + F2 + F3
b exact 2 N. Je kunt de constructie checken door de
hokjes in x-richting en y-richting te tellen. De netto
kracht F1 + F2 + F3 wijst 2 hokjes naar beneden.
De schaal van figuur 6.16: 1 N ⇔ 1 cm.
( F3 is 5 N en is een diagonaal, 32 + 42 = 52 )
13 a
300 N
2 cm 500 N
1,8 cm 4,5 · 102 N en 1,1 cm 2,8 · 102 N
19
2,9 kN. Bij 45° lukt het nog wel zonder tekening.
10 betonblokken
en van 210 kg → Fvert = 2058 N
en Fhoriz = 2058
8 N Fdiagnonaal = 2910 N
som 780 N
20°
6.3 Rekenen met krachten als vectoren
500 N
20 a
45 kN
2 hokjes 100 N
b 7,8 cm lang, dus 780 N
c 8° (grootste kracht → kleinste hoek)
14 a Fz = m · g = 4500 × 9,8 = 4,4 · 104 N
b De pijl is 1,6 cm. Dus de schaal is 2,76 · 104 N per cm.
c De pijl naar rechts is 2.4 cm lang dus 6,6 · 104 N. Naar
links is de pijl 2,4 cm dus F = 6,6 · 104 N
15
Pulsje
16 a/b
Fy
Fx
Remco
1 cm 100 N
Remco 3,7 · 102 N; Karin 1,5 · 102 N
17 a Bootje a neemt de kortste weg en komt ongeveer
recht aan de overkant terecht. Als je de resultante
van de beide snelheden neemt ga je recht naar de
overkant.
b Bootje b is het snelst aan de overkant. Zijn voorwaartse snelheid is recht naar de overkant toe.
Ondertussen drijft hij wel af met de stroom mee en
komt dus niet recht aan de overkant terecht, maar
een stukje stroomafwaarts.
c Bootje c gaat het hardst ten opzichte van de kant.
242759_NAT 3E TF HAVO 4 UW_CH06.indd 66
F = 6,71 N
27,6°
500 N
10°
370 N
66
b 3,85 cm 77 kN
c 77 kN ___________
Fsom = 62,42 + 45,52 = 77 kN
y-richting
N
150
25°
1 cm ^
= 20 N
62 kN
21 a
Karin
auto
Fsom = 77 kN
b Fy = sin · F
Fx = cos · F
x-richting
Fy = sin 27,6° × 6,71 = 3,11 N
Fx = cos 27,6° × 6,71 = 5,95 N
Wanneer je het raster in Figuur 6.27 bekijkt
verwacht je:
Fy = 3,00
Fx = 6,00
De hoek is eerder 26,56°
Fy = sin 26,56° × 6,71 = 3,00 N
Fx = cos 26,56° × 6,71 = 6,00 N
© Noordhoff Uitgevers bv
15/07/13 6:13 PM
Hoofdstuk 6 Kracht als vector
22 a
Ftrek = 65,3 N
25 a
Ftouw
35°
2,2 cm
3,3 cm
1 cm ^
= 20 N
Fwind = 14 N
40°
2,5 cm
1 cm ^
= 20 N
b Fhorizontaal → 2,5 cm 50 N
Fverticaal → 2,2 cm 44 N
c 50,0 N en 44,0 N
Fhorizontaal = 65,3 × cos(40º) = 50,0 N
Fverticaal = 65,3 × sin(40º) = 42,0 N
Fz = 20 N
b 14 N
Fwind
____
23 a In kabel B is de spankracht het grootst.
26°
Fz
B
Fwind = (2,04 × 9,81) × tan 35 = 14 N
c Ftouw is de schuine zijde, dus groter dan Fz
A
6.4 Krachten op de helling
26 a
36°
b tan = 0,1 → = 5,7°
c sin = Fw /Fz → Fw = Fz × sin 5,7 = 1,0 · 103 N.
b 7,5 · 106 N en 10 · 106 N
Fz
= sin ⇒ Fspan = _____
sin
4,4 · 106
Fspan,A = _______ = 7,5 · 106 N
sin 36
4,4 · 106
_______
Fspan,B =
= 10 · 106 N
sin 26
Fz
____
27 a Bij constante snelheid is de netto kracht nul.
6 N F// = Fz · sin =
Fz = m · g = 125 × 9,81 = 1226
1226 × sin 5,7° = 122 N
Fw = 27 N
dus de trekkracht moet 122 + 27 = 149 N zijn.
b Nee, want F// is (veel) groter dan de maximale
weerstandskracht.
Fspan
24
5°
Tekening is
niet op schaal.
Ftrek
α
Fz
Ftrek
____
Fz
= tan ⇒ Ftrek = Fz · tan en
1
sin = __
12 ⇒ = 4,78°
⇒ Ftrek = (800 × 9,81) × tan 4,78°
= 6,6 · 102 N
© Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_CH06.indd 67
10 m
α
100 m
Fz
Fz
= tan ⇒ Fwind = F · tan
28
Een holle is moeilijker. Het steilste stuk is het
moeilijkst te overwinnen. Als dat onderaan zit kun je
je bewegingsenergie van je aanloop gebruiken om
dat te overwinnen. Als de helling bovenaan het
steilst is, is je bewegingsenergie al op als je die
nodig hebt.
29 a De tegenwerkende component van Fz mag
hoogstens zijn:
F// = 2,6 · 103 – 3,4 · 102 = 2,26 · 103 N.
Er geldt F// = Fz sin .
2,26 · 103 = (1240 + 960) × 9,81 · sin
→ sin = 0,1047
→ = 6,0°
b tan = 0,11 → de helling is 11%
30 a F// = Fz sin = 90,0 × 9,81 × sin 15,0° = 229 N
Fw = 48,4 N
Fnetto = 229 – 48,4 = 180 N
Fnetto _____
180
2
a = ____
m = 90,0 = 2,00 m/s
67
15/07/13 12:36 PM
Hoofdstuk 6 Kracht als vector
b Als de slee naar boven beweegt werkt de weerstandskracht naar beneden, dus als de trekkracht
wegvalt is er een netto kracht omlaag van
228,5 + 48,4 = 276,9 N
De vertraging is
Fnetto
____
276,9
_____
a = m = 90,0 = 3,08 m/s :
2
het afremmen duurt dan 1,5 : 3,08 = 0,488 s.
De gemiddelde snelheid tijdens het afremmen is
__
1
2 · vmax = 0,75 m/s
dus hij legt nog 0,75 × 0,488 = 0,366 = 0,37 m af.
c Fn = F = Fz · cos = 90,0 × 9,81 × cos 15° =
8,5 · 102 N. Dit is kleiner dan 8,6 · 102 N .
De slee zakt dus nét niet in de sneeuw. (Maar er
moet geen oneffenheid of zwakke plek in de
sneeuwlaag zitten, want dán...)
Veronderstel dat de slee bovenaan de helling staat:
=0
d Fw,s,max = f · Fn . Fn = Fz = 90,0 × 9,81 = 882,9 N.
Fw,s,max = 0,15 × 882,9 = 132 N.
F
31 a sin = __II → F// = Fz · sin = m · g · sin
Fz
F┴
→ F┴ = Fz · cos = m · g · cos
cos = ___
Fz
b Als groter wordt, dan wordt sin ook groter, dus
F// wordt groter.
Als groter wordt dan wordt cos kleiner, dus F┴
wordt kleiner.
32
Pulsje
33 a Fw,s,max = f · Fn .
Fn = m · g · cos = 250 × 9,81 × 0,99 = 2,4 · 103 N.
Fw,s,max = 160 N dus:
f = Fn /Fw,s,max = 2,4 · 103 /1,6 · 102 = 15,2. Hier hoeft
geen eenheid bij want f heeft geen eenheid.
b
Ft
F⁄⁄
8,0°
8,0°
F⊥
Fz
F// = m · g · sin = 250 × 9,81 · sin 8,0° = 341 N langs
de helling omlaag.
Dat is groter dan de trekkracht van het touw, dus er
moet ook nog een weerstandskracht van 41 N
omhoog zijn.
c Nu is de trekkracht groter dan F// dus de weerstandskracht is nu omlaag gericht:
Ft = F// + Fw → Fw = Ft – F// = 400 – 341 = 59 N
maak desnoods een nieuwe tekening van de
krachten
68
242759_NAT 3E TF HAVO 4 UW_CH06.indd 68
d Bij 600 N is het verschil tussen Ft en F// groter dan
160 N: de kist schuift dus omhoog en de weerstandskracht werkt omlaag en is maximaal:
Fnetto = Ft – F// – Fw = 600 – 341 – 160 = 99 N
Fnetto ____
99
2
a = ____
m = 250 = 0,395 = 0,40 m/s
Bij 100 N is het verschil ook groter dan 160 N, maar
dan ten gunste van F//, dus schuift de kist omlaag: de
weerstandskracht werkt omhoog en is maximaal:
Fnetto = F// – Fw – Ft = 341 – 160 – 100 = 81 N
Fnetto ____
81
2
a = ____
m = 250 = 0,324 = 0,32 m/s
e Zo lang het verschil tussen F// en Ft niet groter is dan
160 N kan de weerstandskracht het verschil opvangen en blijft de kist liggen.
De uitersten zijn dus 341 + 160 = 501 N en
341 – 160 = 181 N.
34 a Als de helling steiler wordt neemt de normaalkracht
af, dus de maximale weerstandskracht ook.
b Op de helling van 23° wordt aan het blokje getrokken met een kracht, F//:
F// = m · g · sin = 0,767 N
Het blokje blijft op zijn plaats wanneer er voldoende
schuifweerstand is bij een hoek van 23°, en dat
hangt samen met de normaalkracht op de helling.
Fw,s,max = f · Fn
Als de plank horizontaal ligt:
Fn = Fz · cos 0° = 1,96 N en Fw,max is dan 0,8 N
f = 1,96/0,8 = 0,41
Bij een hoek van 23°:
Fn = Fz · cos 23° = 1,81 N en Fw,max = ?
Je kunt Fw,s,max uitrekenen
en
Fw,s,max = 0,41 · 1,81 = 0,736 N
Het lijkt er dus op dat het blokje gaat schuiven
omdat F// iets groter is dan Fwmax, maar dat is niet
zeker omdat de maximale schuifweerstand maar
één significant cijfer heeft; dat is te onnauwkeurig
om vast te kunnen stellen welke van de twee
krachten het grootste is.
35 a 0,6 g = 0,0006 kg. 1 cm3 = 0,000001 m3 dus
0,6 gcm–3 = 600 kgm–3.
b Het volume van de sneeuw is 1,8 × 120 × 70 =
1,5 · 104 m3. Iedere m3 heeft een massa van 600 kg
dus in totaal komt er een massa van 9,1 · 106 kg
sneeuw naar beneden glijden.
c F// = m · g · sin = 9,1 · 106 × 9,81 × sin 60 = 7,7 · 107 N
d F = m · a → a = F/m → a = 7,7 · 107/9,1 · 106 = 8,5 ms–2
s = vgem · t = 0,5 · veind · t
veind = a · t. Dus:
s = 0,5 a · t2 → t2 = s/0,5a = 400/(0,5 × 8,5) = 94,1 dus
t = √94,1 = 9,7 s → veind = a · t = 8,5 × 9,7 = 82,5 ms–1
≈ 300 km/h!
© Noordhoff Uitgevers bv
15/07/13 12:36 PM
Hoofdstuk 6 Kracht als vector
Toepassing
8
Opgave 1 Vrachtwagen
1
k = Flucht/v2 [K] = N/m2 · s2 N = kg · m/s2 dus
[K] = kg/m
2
90 km/h = 25 m/s Fmotor = Fluchtweerstand + Frolweerstand
Fmotor = 35,0 × 625 + 3000 = 24875
Fmotor = 24,9 kN, bij 90 km/h
3
Over een lengte van 100 m horizontaal bewegen
gaat de weg 8 meter omhoog. De tangens van die
hoek is dan 8 : 100 = 0,08. Daar hoort een hoek bij
van 4,6 graden.
4
α
8m
100 m
Fmotor
Fz⁄⁄
77 kN onder een hoek van 48°
Er ontstaat een kracht naar links t.g.v. stroming. Die
moet door de rechter sleepboot gecompenseerd
worden naar rechts.
De dwarskracht is 20% van 134 kN, dat is 26,8 kN.
Naar rechts levert deze boot: 30 + 26,8 = 56,8 kN.
Naar voren levert deze boot nog steeds 52 kN.
Ftotaal is dan (pythagoras) 77 kN.
(De boot vaart nu onder een hoek van 48°)
Het zou effectiever zijn wanneer beide boten hun
richting behouden terwijl de rechter boot veel meer
kracht gaat leveren en de linker boot iets minder.
Met een constructie of met twee vergelijkingen en
twee onbekenden is dit op te lossen.
Opgave 3 Bungee-trampoline
9
F = 3,6 · 102 N (met een marge van 0,2 · 102 N) Zie ook
de tekening.
4,6°
Fz = 294 kN
Fz// = 23 kN
Fmotor = 29 kN
3,6·102 N
Fz
Fw,r = 3,0 kN is niet op schaal te tekenen
Fw,l = 2,5 kN is niet op schaal te tekenen
6
Hellingsgraad = 8%
= 4,59°
59° sin = 0,080
(bij kleine hoeken, sin = tan )
Krachten langs de helling:
Fz · sin = 30000 · 9,8 · 0,08 = 23,5 kN.
N
Fw,r = 3,0 kN
Fmotor = 29 kN Fw,l = 29 – 23,5 – 3,0 = 2,5 kN
Fw,l = 35 · v2 v = √2500/35 = 8,45 m/s = 30 km/h
Als de auto niet zo hard rijdt kan de motor ook niet
zoveel toeren maken, dus wanneer hij langzaam de
helling op rijdt is het fijn dat er ook bij weinig toeren
veel motorkracht beschikbaar is.
Opgave 2 Booreiland verslepen
7
88 kN en 134 kN
De rechter sleepboot trekt
600 kN
met een kracht van 30 kN naar
rechts.
(60·sin 30° = 30 kN )
20°
Dit moet door de linker
30°
sleepboot weer opgeheven
worden om de sleep rechtuit
te laten varen.
F · sin
s 20° = 30 kN
F = 88 kN
Het eiland heeft een weerstand die in grootte gelijk is
aan de trekkracht van beide boten recht vooruit.
88 · cos20° + 60 · cos30° = 82 + 52 = 134 kN.
© Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_CH06.indd 69
2·102 N
4,7·102 N
10
Δh = 4,6 m (met een marge van 0,4 m)
Bepaling:
Als de snelheid nul is, bevindt Lisa zich in het
hoogste of in het laagste punt. Het hoogteverschil is
dus gelijk aan de oppervlakte onder de grafiek
tussen twee nuldoorgangen.
Deze oppervlakte kan benaderd worden met een
driehoek of een rechthoek en is gelijk aan 4,6 m.
v in m/s
5
1 cm
5
4
3
2
1
0
–1
–2
–3
–4
–5
1
2
3
4
5
6
t in s
7
69
15/07/13 12:36 PM
Hoofdstuk 6 Kracht als vector
Lisa bevindt zich in het hoogste punt als de snelheid
nul is en als de snelheidsgrafiek daalt.
v in m/s
11
Er kan dan nog geen water rechts langs de boot
stromen. De kracht is het grootst vlak voor aankomst. De stroming rechts langs de boot is dan het
grootst.
5
4
3
2
1
0
–1
–2
stroomrichting van het water
–3
–4
–5
gierketting (kort)
1
2
3
4
5
6
t in s
7
De versnelling die Lisa dan ondervindt, is gelijk aan
de steilheid van de raaklijn in dat punt aan de
grafiek.
–5–5
–2
De steilheid is gelijk aan _____
2,3–0,7 = (–)6,3 ms
Deze (absolute) waarde is kleiner dan de
(absolute) waarde van de gravitatieversnelling
g = (–)9,8 ms–2.
Dus moeten de elastieken nog een kracht uitoefenen op Lisa.
Opgave 4 Tuibrug
12
Het brugdeel heeft een massa van 1200 kg. Dus
werkt er een zwaartekracht op van 1200 × 9,81 =
11,8 kN.
De tuidraden trekken onder een hoek van 30 graden
met de verticaal dus voor de kracht Ftuidraden geldt:
Ftuidraden = Fz/cos 30 = 13,7 kN.
13
Ftuidraden = Fz/cos 45 = 16,6 kN
14
Bij een hoek van 80° is de kracht in de kabels 68 kN
(zelfde formule weer gebruiken). Dat is een factor 4
groter dan de kracht bij een hoek van 45°. Bij grote
hoeken neemt de belasting sterk toe.
15
16
gierketting (lang)
N
18
De veerman moet de de korte en de lange kant van
de gierketting aan de pont juist omdraaien. Het
water stroomt aan de linker kant langs de boot, en
de reactiekracht van het water op de boot is naar
rechts.
19
De kracht van het water op de boot is schuin naar
beneden. Er is een component in de stroomrichting en
er is een component loodrecht daarop, door het water
dat om de boot heen stroom. (Het is enigszins vergelijkbaar met de werking van een vliegtuigvleugel).
stroomrichting van het water
gierketting (kort)
De lineaire uitzettingscoëfficiënt geeft aan hoe veel
(meter) een stuk kabel van een meter lengte uitrekt
bij een temperatuurstijging van 1 graad. De eenheid
is daarom in K–1.
De kabel was 10 m lang bij 25 graden Celcius. Bij min
10 graden Celcius is het temperatuurverschil 35
graden. Per meter krimpt de kabel 2 · 10 –6 m per
graad temperatuurdaling. Voor 10 meter bij 35
graden geldt: 350 × 2 · 10 –6 m krimp ofwel 0,0007 m
ofwel 0,7 mm wordt de kabel korter.
Opgave 5 Gierpont
17
Doordat de boot scheef ligt stroomt het water
geforceerd langs de achterkant van de boot.
In de tekening is dat rechts. Het water wordt dus
rechts langs de boot geduwd en door de reactiekracht wordt de boot naar links geduwd. Dat gaat
het slechtst bij het vertrek van de rechter wal.
70
242759_NAT 3E TF HAVO 4 UW_CH06.indd 70
gierketting (lang)
N
De kracht van de boot op het ankertouw heeft
dezelfde richting. Deze schuine kracht kun je
vervolgens ontbinden in de richtingen van de
gierkettingen.
20
Wanneer een boot zicht voorttrekt aan een kabel
die van de ene oever naar de andere loopt gaat de
kabel aan de voorzijde strak staan. Je kunt alleen
achter de pont langsvaren want daar zakt de kabel
weer naar de bodem. Bij een gierpont blijft de
vaarweg altijd minimaal voor de helft vrij.
© Noordhoff Uitgevers bv
15/07/13 12:36 PM
Hoofdstuk 6 Kracht als vector
21
Wanneer de pont nog aan de kant ligt is er bijna
geen krachtcomponent in de vaarrichting omdat er
geen water om de boot kan stromen. Een hulpmotor helpt dan de pont bij de kant weg te krijgen,
waarna de kracht waarmee het water de pont naar
de overkant duwt steeds groter wordt.
3 a
F2
5,8 cm
F1
5,1 cm
30°
Proefwerkopgaven
10°
1 a
leeftijd
scalar
lengte
scalar
zwaartekracht
vector
1 cm ^
=2N
Fz
b 1,7 · 102 N
Fz = m · g = 0,780 × 9,81 = 7,65 N
F1 = 5,8 × 2 = 11,6 = 12 N
F2 = 5,1 × 2 = 10,2 = 10 N
b Beide krachten in de koorden, 10 N en 12 N, zijn (veel)
kleiner dan 1 kN. Zie tekening!
1,7·102 N
40°
40°
y
Ftrek
h
260 N
Ftrek
____
260
= sin 40° ⇒
Ftrek = 260 × sin 40° = 1,7 · 102 N
c Fspan = 260 × cos 40° = 2,0 · 102 N
d 47 cm
h = 2,0 – y
y = 2,0 × cos 40° = 1,53
⇒ h = 2,0 – 1,532 = 0,47 m
4 a Fw,s,max = f · Fn Totale massa = 47 kg
Fn = m · g · cos = 47,0 × 9,8 × cos 2,9 = 460 N
Fw moet even groot zijn als de kracht langs de
helling en die is Fz · sin = 47,0 × 9,8 × sin 2,9 =
23,3 N. f = Fw/Fn = 23,3 : 460 = 0,051 (geen eenheid)
b Als de snelheid constant is, is de kracht langs de
helling even groot als de wrijvingskracht.
De kracht langs de helling is gelijk aan Fz · sin =
47,0 × 9,8 × sin 6,0 = 48 N
5
F// aan de linker kant moet dan gelijk zijn aan F//
rechts.
F// = Fz · sin
Links geldt dan: 5,0 × 9,81 × sin 70 = 46,1 N.
Rechts geldt: 7,2 × 9,81 × sin 55 = 57,9 N.
Er is dus geen evenwicht en B zal naar beneden
schuiven en A omhoog trekken.
Er is in totaal 12,2 kg aan massa en een netto kracht
van 57,9 – 46,1 = 11,8 N. Dat geeft een versnelling
(F = m · a) van 11,8 : 12,2 = 0,97 ms–2.
2 a
9,8 kN
5,3 kN
5,3 kN
b a = F/m a = 9,8 · 103 : 250 = 39,2 ms–2 ..dat is 4 g!
© Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_CH06.indd 71
71
15/07/13 12:36 PM
Hoofdstuk 7 Energie Omzetten
Hoofdstuk 7
Energie Omzetten
1
2
Introductie
Enkele manieren: rillen, bloed verplaatsen van huid
naar binnenste van lichaam, haartjes op de huid
recht omhoog zetten (‘kippenvel’).
Als je weinig beweegt hoeft je lichaam weinig
voedingstoffen te verbranden om je lichaam te
laten bewegen. Dit verbranden zorgt er juist voor
dat je opwarmt.
3
Eigen antwoord
4
Mogelijke antwoorden:
- Als je meer gaat bewegen, wordt vet omgezet in
spierweefsel. Hierdoor neemt ook je ruststofwisseling toe. Dus ook als je niet beweegt, val je nog
af. (als je tenminste niet meer gaat eten)
- Verder zorgt de toename van spierweefsel er ook
voor dat je makkelijker beweegt en dus eerder
geneigd bent meer te bewegen.
- Minder eten heeft bovendien tot gevolg dat je
lichaam zorgvuldiger met de geringe hoeveelheid
voedsel omgaat en daar meer calorieën uit haalt. Dan
moet je nog minder gaan eten om nog af te vallen.
- Bovendien loop je met dieet het risico dat je
voeding minder uitgebalanceerd raakt wat minder
goed voor de gezondheid is.
- Veel bewegen is goed voor je hart en vaatstelsel
- Het schijnt ook beter te zijn voor botten en
gewrichten.
5 a Zijn lichaam kan beter tegen lage temperaturen en
hoeft dus ook niet extra voedingsstoffen te gaan
verbranden om warm te blijven. Daarom heeft hij
stilzittend niet veel last van de kou.
b Bruinvet is een type vetweefsel dat warmte kan
produceren door de oxidatie van vet. Hierdoor
produceert het lichaam dus warmte en kan hij
daarom langer tegen de kou.
6
Als je een grafiek maakt van de snelheid tegen de
energie wordt duidelijk dat het een lineair verband is.
Je kan een rechte lijn trekken door de meetpunten.
energie in kJ per kg per uur
80
70
Nee. Als je langzaam wandelt doe je langer over de
terugreis, maar verbruik je ook minder energie per
uur.
8 a Eigen antwoord
b Eigen antwoord
7.1 Energiesoorten
1 a Reken eerst de snelheid om in m/s:
90 km/h = 25 m/s. Dan de formule invullen:
Ek = _21 mv2 = _21 × 12 · 103 × 252 = 3,75 · 106 J
= 3,8 · 106 J
b Ek = _21 mv2 invullen:
5,0 · 1012 = _21 × m × 120002 = 72 · 106 × m
5,0 · 1012
m = _______
= 6,9 · 104 kg
72 · 106
Bedenk dat 12 km/s = 12000 m/s, maar onthoud dat
het getal 12 slechts 2 significante cijfers heeft.
c 15 g = 0,015 kg
Ek = _21 mv2 invullen:
5,0 · 103 = _21 × 0,015 × v2 = 0,0075 × v2
_______
5,0 · 103
2
v = _______
0,0075 = 8,2 · 10 m/s
2
Pulsje
3 a Ez = mgh = 4,0 · 104 × 9,81 × 600 = 2,4 · 108 J
b Met 2,4 · 108 J
Als er geen weerstand is wordt alle zwaarte-energie
omgezet in kinetische energie.
c 1,1 · 102 m/s = 3,9 · 102 km/h
Ek = _21 mv2 invullen:
2,35 · 108 = _21 × 4,0 · 104 × v2 = 2,0 · 104 × v2
________
v=
2,35 · 10
________
8
2,0 · 104
= 1,1 · 102 m/s inhet dal.
d De skiër komt met dezelfde 110 m/s aan in het dal.
Boven op de helling heeft de skiër alleen zwaarteenergie:
Ez = mgh = 80 × 9,81 × 600 = 4,7 · 105 J
Al deze zwaarte-energie is in het dal omgezet in
kinetische energie.
Ek = _21 mv2 invullen:
4,7 · 105 = _21 × 80 × v 2 = 40 × v 2
________
60
4,7 · 105
2
v = _______
40 = 1,1 · 10 m/s
50
40
30
20
10
0
7
0
72
242759_NAT 3E TF HAVO 4 UW_CH07.indd 72
5
10
15
20
snelheid in km/h
Je kunt dit ook zien als je eerst de formule Ek +
Ez = constant invult:
Ek + Ez (boven) = Ek + Ez (beneden) →
1
2
mgh = __
2 mv
© Noordhoff Uitgevers bv
15/07/13 12:46 PM
Hoofdstuk 7 Energie Omzetten
b 14 m/s (= 52 km/h)
Je kunt nu links en rechts delen door m.
Met andere woorden: alleen de hoogte en de waarde
van g bepalen de snelheid waarmee je beneden komt, de
massa speelt geen rol voor de uitkomst.
4
Dus:
6,5 · 1013 J
Gemiddeld daalt het water over 6 m hoogte.
Het volume water dat uitstroomt bedraagt:
V = Ah = 55 · 106 × 6 = 3,3 · 108 m3
De massa van dat water = dichtheid × volume:
m = · V = 998 × 3,3 · 108 = 3,3 · 1011 kg.
De gemiddelde hoogte van het water is 20 m.
De vrijkomende zwaarte-energie bedraagt:
Ez = mgh = 3,3 · 1011 × 9,81 × 20 = 6,5 · 1013 J
5
Pulsje
6
Pulsje
7
11 m/s = 39 km/h
Er is niet gegeven hoe zwaar de auto is, maar bij
opdracht 3 heb je gezien dat de massa er niet toe
doet. Je kunt dus gewoon doen alsof de auto een
massa heeft van 1 kg.
Zie de ‘Zo doe je dat’:
Maak een schets en noem het punt waar de auto van
de kade afrijdt A en waar hij in het water plonst B.
Het nulniveau kies je bij het wateroppervlak.
Schrijf alle gegevens erbij.
In A: v = 30 km/h = 8,33 m/s → Ek = _21 mv 2 =
0,5 × 1 × 8,332 = 34,7 J
h = 2,4 m → Ez = mgh = 1 × 9,81 × 2,4 = 23,5 J In B:
h = 0 m dus Ez = 0 J
De totale energie is 34,7 + 23,5 = 58,2 J
dus Ek in B is 58,2 J
58,2 = _21 × 1 × v2 → v2 = 116,4 → v = 10,8 =
11 m/s (= 39 km/h)
8
De snelheid waarmee het treintje de looping verlaat is de
snelheid in punt A, omdat A het begin én het einde van
de looping is.
De massa weet je niet, maar die zal waarschijnlijk
weer wegvallen uit de vergelijkingen. In de formule
laat je m staan. De beginenergie is in alle drie de
situaties even groot namelijk een kinetische energie
ter grootte _21 m 52 = 12,5 × m en een hoogte-energie
met een waarde van mgh = m × 9,81 × 15 = 147 × m.
Totaal is dat een energie van 160 × m. Op de grond is
dat omgezet in kinetische energie, waarbij v de
snelheid op de grond is.
De massa valt weer weg in het linker en rechterdeel
van de vergelijking:
160 × m = _21 mv2 → 160 = _21 v2 → v 2 = 319
→ v = 18 m/s (= 64 km/h)
9 a 18 m
In A: v = 75 km/h = 20,83 m/s; h = 0 m.
In B: v = 32 km/h = 8,9 m/s; h = ? m.
Stel nu de massa op 1 kg en vul in:
Ek (in A) = Ek + Ez (in B)
__
1 2 __1 2
2 vA = 2 vB + gh ⇒
__
__
1
1
2
2
2 × 20,8 = 2 × 8,9 + 9,81 × h ⇒
217,01 – 39,51
h = ____________ = 18 m
9,81
© Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_CH07.indd 73
B: h = 11,5 m
VB = ? m/s
A: h = 0 m; VA = 20,8 m/s
De totale energie is nog steeds 217 J;
de zwaarte-energie in B is Ez = mgh =
1 × 9,81 × 11,5 = 112,8 J
dus Ek = 217 – 112,8 = 104,8 J
_1
2
2 × 1 × v = 104,8 → v = 14,4 m/s = 14 m/s
(= 52 km/h)
10
Pulsje
11 a
A
h = 15 m
B
Noem de meest linkse stand van het schip A en de
onderste stand B. Als hij precies 90° draait is het
hoogteverschil 15 m.
In A:
Ez = mgh = 2,5 · 103 × 9,81 × 15 = 3,68 · 105 J
b 17 m/s
In A:
Ez = 3,68 · 105 J en Ek = 0 J
In B:
Ez = 0 J
dus Ek moet 3,68 · 105 J zijn
_1
2
5
2 m · v = 3,68 · 10 J
_1
3
2
5
2 × 2,5 · 10 × v = 3,68 · 10 J → v = 17,2 =
17 m/s.
ook hier mag je de massa wegdelen of op 1 kg stellen.
c α = 70°
A
α
a
C
h
B
Noem het gezocht punt C.
Om de hoek te kunnen berekenen moet je eerst de
hoogte weten.
Ook in C is de totale energie 3,68 · 105 J
Ek = _21 mv2 = _21 × 2,5 · 103 × 102 = 1,25 · 105 J
dus Ez = 3,68 · 105 – 1,25 · 105 = 2,43 · 105 J
mgh = 2,43 · 105 J → h = 9,9 m
De hoek in de getekende driehoek kun je berekenen met behulp van de cosinus:
de aanliggende zijde a is 15 – 9,9 = 5,1 m
dus cos = a/s = 5,1 : 15 = 0,34 → = 70°.
d Je berekent weer eerst de zwaarte-energie.
Daarvoor moet je eerst de hoogte h berekenen:
sin 30° = h/15 dus: h = 15 × sin 30° = 7,5 m.
73
15/07/13 12:46 PM
Hoofdstuk 7 Energie Omzetten
De hoogte van punt A boven punt B is 15 m + 7,5 m
= 22,5 m.
A
h
nog een deel over: 3,75 · 106 J – 2,94 · 106 J =
0,81 · 106 J = 8,1 · 105 J.
Die overblijvende energie wordt door de remmen
omgezet in warmte.
c Bij het optrekken kan de zwaarte-energie (heuveltje af)
weer gebruikt worden om op gang te komen.
d Ek = Ez
_1
2
2 mv = mgh
__1 2
v
=
gh
2
v2 = 2 gh = 2 × 9,81 × 25 = 491
v = 22 m/s
15 m
30°
90°
B
Ez = mgh = 2,5 · 103 × 9,81 × 22,5 = 5,52 · 105 J
In het onderste punt (B) geldt:
Ek = _21 mv2 = _21 × 2,5 · 103 × v2 = 5,52 · 105 J
v2 = 441,45 en v = 21 m/s
De snellere methode:
energieën gelijk stellen ...
Ez = Ek
... en massa m wegstrepen
mgh = _21 mv2
gh = 2_1 v2
v2 = 2 gh = 2 × 9,81 × 22,5 = 441,45
v = 21 m/s
12 a Potentiële energie (veerenergie)
b 5,1 m
Ga er van uit dat alle kinetische energie wordt
omgezet in zwaarte-energie.
__
1 2
100
___
__
v2 _____
1
2
2 mv = mgh ⇒ 2 v = gh ⇒ h = 2 g = 19,62 = 5,1 m
De uitkomst betekent dat de springer zijn zwaartepunt 5,1 m hoger kan brengen. Omdat zijn zwaartepunt zich circa 1 m boven de grond bevindt tijdens zijn
aanloop, kan hij zijn zwaartepunt op een hoogte van
6,1 m brengen. De rest is een kwestie van techniek.
c Eveer = 1,25 · 103 J
Maak weer gebruik van het gelijk blijven van de som
van kinetische en potentiële energie:
__
1
1
2 __
2
2 mvA= 2 mvB + Eveer + mgh
__
1
2
2
2 × 70 × 10 = 2 × 70 × 5 + Eveer + 70 × 9,81 × 2
__
1
3500 = 875 + Eveer + 1373
Eveer = 3500 − 875 − 1373 = 1252 J = 1,25 · 103 J
d De veerenergie is niet afhankelijk van de massa van
de springer, maar van de eigenschappen (veerconstante) van de veer. Omdat de zwaarte-energie en
de kinetische energie beide evenredig zijn met de
massa van de springer, moet je de massa weten om
de veerenergie uit te kunnen rekenen.
13
pulsje
14
407 km/h
Binas: massa van een nijlpaard is 3000 kg.
massa huismus is 35 g.
__1
_1
2
2
2 mnijlpaard v = 2 mmus v invullen:
_1
_1
2
×
3000
×
5
=
×
35
·
10−3 v2
2
2
v2 = 37500/0,0175 = 2142857
v = 1464 m/s = 407 km/h
15 a Ek = _21 mv2 = _21 × 12 · 103 × 252 = 3,75 · 106 J
b toename zwaarte=energie is gelijk aan:
Ez = mgΔh = 12 · 103 × 9,81 × 25 = 2,94 · 106 J
Van de kinetische energie die je bij vraag a hebt
uitgerekend blijft na het omhoog gaan van de trein,
74
242759_NAT 3E TF HAVO 4 UW_CH07.indd 74
16 a De hoogte van de Mount Everest is 8848 m. De
gemiddelde temperatuur lees je af uit de grafiek:
–42 °C
b Op 0 m is de temperatuur 15 °C
Op 8000 m is de temperatuur –37 °C
Conclusie: bij een stijging van 8000 m daalt de
temperatuur met 52 °C.
Per 100 m stijging is dat: 52/80 = 0,65 °C per 100 m.
c Hoe hoger de temperatuur, hoe hoger de bewegingsenergie.
17
7.2 Optrekken en afremmen
45 km/h
Bereken eerst de verrichte arbeid:
W = F · s = 3 × 1,5 = 4,5 J
Deze arbeid wordt omgezet in kinetische energie:
4,5 = _21 × 0,058 × V2 ⇒
______
4,5
v = ______
0,029 = 12,46 = 12 m/s = 45 km/h
18 a 1,1 kN
Ek (begin) = 0 J (de kogel staat stil)
Ek (eind) = _21 mv2 = _21 × 7,26 × 14,52 = 763,2 J
de toename is 763,2 J, dus de arbeid ook:
763,2 = F · s = F × 0,75 → F = 763,2: 0,75 = 1018 =
1,0 · 103 N
b Ten eerste verleng je de afstand waarover je kracht
uitoefent op de kogel. Ten tweede maak je gebruik
van je schouder- en rug- en beenspieren, die veel
sterker zijn dan je armspieren, waardoor je een
grotere kracht kunt uitoefenen.
19 a v (begin) = 100 km/h = 27,8 m/s
Ek (begin) = _21 mv2 = 3,28 · 105 J
Ek (eind) = 0 J
de afname van Ek , dus de arbeid is 3,28 · 105 J
3,28 · 105 = F · s = F × 40 → F = 8,2 · 103 N
b 10 m
nu is vbegin = 13,9 m/s → Ek (begin) = _21 mv2 = 8,20 · 104 J
de arbeid is nu dus 8,20 · 104 J
8,20 · 104 = F · s = 8,20 · 103 × s → s = 10 m
c De kinetische energie bij 50 km/h is 4 maal zo klein
als bij 100 km/h; de (negatieve) arbeid die nodig is
om de auto te stoppen is dus ook 4 maal zo klein.
Bij dezelfde remkracht is dan ook de remafstand
4 maal zo klein, dus 40 : 4 = 10 m
20 a 8,3 kN
54 km/h = 15 m/s
v (begin) = 54 km/h = 15 m/s
© Noordhoff Uitgevers bv
15/07/13 12:46 PM
Hoofdstuk 7 Energie Omzetten
Ek (begin) = _21 mv2 = 1,24 · 105 J
Ek (eind) = 0 J
de afname van Ek, dus de arbeid is 1,24 · 105 J
1,24 · 105 = F · s = F × 15 → F = 8250 = 8,3 · 103 N
b 0,67 s
De auto legt gemiddeld 10 m af voordat de
bestuurder begint met remmen. De reactietijd
bedraagt dus t = s/v = 10/15 = 0,67 s
c 24 km/h
Voordat de bestuurder nu begint met remmen zijn
er 0,87 s verstreken. De auto legt in die tijd s = vt =
0,87 × 15 = 13 m af. De auto wordt daarna 12 m
afgeremd voordat de voetganger wordt geraakt.
De (negatieve) arbeid is dan F · s = 8250 × 12 = 99 · 103 J
Ek (begin) was 1,24 · 105 J
dus Ek (eind) = 1,24 · 105 – 99 · 103 = 25 · 103 J
25 · 103 = _21 mv2 = _21 × 1,1 · 103 × v2 → v = 6,7 m/s
(= 24 km/h)
21 a 26 m/s
De netto voorwaartse kracht bedraagt
95 – 14 = 81 kN Daaruit volgt:
W = F · s = 81 · 103 × 500 = 405 · 105 J
Ek (begin) = 0 J dus Ek (eind) = 405 · 105 J
_1
_1
2
5
3
2
5
2 mv = 405 · 10 → 2 × 120 · 10 × v = 405 · 10
hieruit volgt v = 26 m/s (= 94 km/h)
b Op 2,0 km afstand
Om de snelheid te verdubbelen moet vier maal zo
veel arbeid worden verricht want Ek is dan vier maal
zo groot. Als de netto kracht gelijk blijft, moet de
verplaatsing dus vier maal zo groot zijn.
22 a 24 m/s
Ez = mgh = 1200 × 9,81 × 30 = 3,53 · 105 J
Al deze zwaarte-energie is beneden omgezet in
kinetische energie.
Ek = _21 mv2 invullen:
3,53 · 105 = _21 × 1200 × v2 = 600 × v2
________
3,53 · 105
v = ________ = 24,3 = 24 m/s
600
De kracht is dus 50 maal zo groot, dus 4500 N
Je kunt ook de verrichte arbeid delen door de
verplaatsing: 1125 : 0,25 = 4500 N = 4,5 kN.
24 a W = Fs = 120 × 0,30 = 36 J
b 90 cm
De drie touwdelen die over de katrollen lopen
moeten elk 30 cm korter worden. Je moet dus 90 cm
touw inhalen.
c 40 N
De afstand waarover je moet trekken is drie maal
groter geworden; de kracht die je nodig hebt is dan
drie keer kleiner: geen 120 N maar slechts 40 N.
25
26 a De zwaartekracht (naar beneden) en de veerkracht
van het elastiek (naar boven) omdat het tussen R en
S uitrekt.
b In punt S. De snelheid verandert niet want die is
maximaal. De versnelling is dus nul en er is evenwicht van de twee krachten (F = ma). Dezelfde
redenering geldt ook voor punt E.
c Tussen R en S is de beweging versneld. De zwaartekracht is in dit deel groter dan de veerkracht van het
elastiek. De maximale snelheid heeft Koos pas in
punt S.
d Tussen S en D is de beweging vertraagd. De zwaartekracht is in dit deel kleiner dan de veerkracht van
het elastiek. De snelheid wordt kleiner totdat Koos
in punt D snelheid 0 heeft.
e De zwaarte-energie wordt eerst volledig omgezet in
kinetische energie totdat het elastiek uitrekt na
15 m. Vanaf dat moment gaat een deel van de
afnemende zwaarte-energie naar de veerenergie.
Ook de kinetische energie neemt af doordat het
elastiek Koos afremt. Na 35 m vallen is alle zwaarteenergie omgezet in veerenergie en is de kinetische
energie weer nul.
25
b 6 · 10 J
In plaats van 3,53 · 105 J is er in werkelijkheid
Ek = 0,5 × 1200 × 22,12 = 2,93 · 105 J bewegingsenergie
na 30 m vallen.
Er is dus 0,6 · 105 J = 6 · 104 J verloren gegaan.
c 2 kN
De weerstandskracht verricht de negatieve arbeid,
die bij b berekend werd: W = Fs ⇒ 60000 =
F × 30, dus F = 2000 N = 2 kN gemiddeld.
E in kJ
4
23 a 1,1 · 10 J
Bereken eerst de totale afstand die je de stang moet
verplaatsen. Om de auto 25 cm omhoog te krikken
moet je 250/4 = 62,5 keer de stang omlaag duwen.
Daarbij legt je hand een afstand van
62,5 × 0,20 = 12,5 m af. De verrichte arbeid is dan
W = Fs = 90 × 12,5 = 1125 J = 1,1 · 103 J.
b 4,5 kN
Volgens de gulden regel is de kracht zoveel maal
groter als de verplaatsing kleiner is. Per slag gaat de
auto 200/4 = 50 maal minder omhoog dan je hand.
242759_NAT 3E TF HAVO 4 UW_CH07.indd 75
Ez
Ev
20
15
10
5
0
3
© Noordhoff Uitgevers bv
Pulsje
0
5
10
15
20
25
30
x in m
35
f Punt E en punt S liggen op dezelfde hoogte. In punt
S is de snelheid maximaal. De afstand waarbij de
kinetische energie maximaal is, lees je af uit de
grafiek: 22 m.
27
Hieruit kun je afleiden dat de baan van Pluto geen
cirkel is. Bij een cirkel met de Zon in het middelpunt,
staat de zwaartekracht steeds loodrecht op de
planeetbaan. De zwaartekracht kan dan niet remmen
of versnellen en de snelheid blijft constant (in grootte).
75
15/07/13 12:46 PM
Hoofdstuk 7 Energie Omzetten
28
7.3 Meer arbeid
tot 25 m. Die lijn ligt ongeveer bij 1,2 kN. Het
antwoord wordt dan: 1,2 × 25 = 30kJ
Pulsje
29 a Na 100 m is de fietser 4,0 m gedaald. De arbeid is
dan gelijk aan de zwaartekracht maal de gedaalde
afstand is: W = F × s = mg × s = 80 × 9,81 × 4,0 =
3139 J = 3,1 kJ
b De bewegingsenergie op het moment dat de fietser
stopt met trappen is: Ek = _21 mv2 = 0,5 × 80 × 36 =
1440 J. Hoe ver stijgt hij daarmee in verticale
richting? De bewegingsenergie wordt dan helemaal
omgezet in zwaarte-energie:
mgh = 1440
80 × 9,81 × h = 1440
h = 1,8 m
Hoeveel meter rijdt de fietser dan door? Dat bereken
je met een verhoudingstabel:
afstand
100 m
25 m
25 × 1,8
hoogteverschil
4,0 m
1,0 m
1,8
De afstand die de fietser nog aflegt is 25 × 1,8 = 45 m.
30 a De arbeid is de kracht in de bewegingsrichting maal
de afstand. De kracht in de bewegingsrichting is
Fx = 110 × cos 35 = 110 × 0,82 = 90 N.
110 N
35°
Fw = 70 N
Fx
W = F × S = 90 × 20 = 1800 J = 1,8 kJ.
b De (negatieve) arbeid van de weerstandkracht:
W = F × s = −70 × 20 = −1400 J = −1,4 kJ.
c De toename van bewegingsenergie is 1800 J − 1400 J =
400 J. Deze toename is omgezet in
bewegingsenergie:
Ek = _21 mv2 = 400 J
_1
2
2 × 40 × v = 400 J
2
v = 20 en v = 4,5 m/s.
d Toename bewegingsenergie: Fx × 20 − 70 × 20
Bij een hoek van 25° wordt dat:
110 cos 25° × 20 − 70 × 20 = 574 J en de snelheid die
daar bij hoort: Ek = _21 mv2 = 574 J
_1
2
2 × 40 × v = 574 J
v2 = 28,7 en v = 5,4 m/s.
Bij een hoek van 45° wordt dat:
110 cos 45° × 20 − 70 × 20 = 156 J en de snelheid die
daar bij hoort: Ek = _21 mv2 = 156 J
_1
2
2 × 40 × v = 156 J
2
v = 7,8 en v = 2,8 m/s.
Conclusie: moeder kan het beste de slee trekken
met een zo’n klein mogelijke hoek.
31 a Het aantal hokjes onder de kromme is 60. Één hokje
is 0,2 kN bij 2,5 m.
b Eén hokje stelt een arbeid voor van 200 × 2,5 = 500 J.
De arbeid over 25 m is 60 × 500 = 30000 J = 30 kJ.
c Trek lijnstuk AB zodanig dat de kracht die bij het
lijnstuk hoort ongeveer de gemiddelde kracht is van 0
76
242759_NAT 3E TF HAVO 4 UW_CH07.indd 76
32 a De arbeid die de veerkracht verricht, is gelijk aan het
oppervlak onder de grafiek: _21 × basis × hoogte =
0,5 × 0,05 × 10 = 0,25 J.
b Deze veerenergie wordt omgezet in bewegingsenergie:
Ek = _21 mv2 = 0,25 J.
_1
2
2
2 × 0,005 × v = 0,25 → v = 100 → v = 10 m/s.
c De veerenergie wordt nu omgezet in hoogte-energie:
mgh = 0,25 J → 0,005 × 9,81 × h = 0,25 → h = 5,1 m.
d Zo’n erwt gaat best hard 10 m/s = 36 km/h.
33 a We gebruiken weer eens een verhoudingstabel:
kracht
4,0 N
0,04 N
0,04 × 15 N
uitrekking
1,0 m
1,0 cm
15 cm
De kracht die nodig is, is 0,04 × 15 N = 0,60 N.
b 0,045 J
De veerenergie reken je uit met de formule:
Ev = _21 Cu2 = 0,5 × 4,00 × 0,152 = 0,045 J.
c 21 m/s
De bewegingsenergie is dan gelijk aan de veerenergie:
_1
_1
2
2
2 mv = 0,045 → 2 × 0,00020 × v = 0,045 →
2
0,00010 × v = 0,045 → v2 = 0,045/0,0001 = 450 →
v = 21 m/s.
34 a 19,4 J
De maximale kracht op het einde is 194 N. In het
begin is die kracht 0 N, want kracht is evenredig met
de uitrekking. De gemiddelde kracht tijdens die
20 cm uitrekking is de helft van 194 N is 97 N.
Arbeid W = Fgemiddeld s = 97 × 0,20 = 19,4 J.
b 40 m/s
De bewegingsenergie van de steen is gelijk aan de
arbeid die je hebt verricht om hem 20 cm uit te
rekken: 19,4 J.
De bewegingsenergie die de steen krijgt bij het
wegschieten bedraagt:
_1
2
2
2 mv = 0,5 × 0,024 × v = 19,4 → v = 40 m/s.
c v = 39 m/s
De kinetische energie is nu voor een deel omgezet in
hoogte-energie mgh = 0,024 × 9,81 × 6 = 1,41 J.
Van de bewegingsenergie van 19,4 J blijft nog over
19,4 − 1,41 = 18 J.
Dat komt overeen met de snelheid:
_1
2
2
2 mv = 0,5 × 0,024 × v = 18 J.
0,012 × v2 = 18 → v2 = 18 / 0,012 = 1500 en
v = 39 m/s.
35 a De gemiddelde kracht Fgem is 2,3 N.
b De arbeid die ze dan verricht is:
W = Fgems = 2,3 × 0,20 = 0,46 J.
c De veerenergie in het elastiek is gelijk aan de arbeid
die Carthy heeft moeten verrichten om het 20 cm
uit te rekken, dus 0,46 J.
36 a De auto die hoort bij de minst spitse boog. In die
grafiek lees je af dat de botstijd langer is (0,47 s) dan
in de andere grafiek (0,31 s). Een langere tijd die
nodig is om tot stilstand te komen, duidt op een
betere kreukzone.
© Noordhoff Uitgevers bv
15/07/13 12:46 PM
Hoofdstuk 7 Energie Omzetten
37 a Tot een uitrekking van ongeveer 0,62 m is de grafiek
een rechte lijn. Dus tot 0,62 m voldoet het touw aan
de wet van Hooke.
b 30 kN/m
De veerconstante is de kracht die nodig is om het
touw 1,0 m uit te rekken: C = F/u = 6000/0,20 =
30000 N/m = 30 kN/m.
c 600 J
De energie die daar voor nodig is, is de veerenergie
van het uitgerekte touw:
Ev = _21 Cu2 = 0,5 × 30000 × 0,22 = 600 J.
d Bereken eerst de kinetische energie die de vallende
klimmer krijgt na een val van 4,0 m. Die kinetische
energie is gelijk aan de afname van zwaarteenergie: mgΔh = 90 × 9,81 × 4 = 3532 J. Het touw
neemt die energie op doordat het uitrekt. De
veerenergie van het touw is dan 3532 J.
Ev = _21 Cu2 = 0,5 × 30000 × u2 = 3532 J
u2 = 3532 / 15000 = 0,235
u = 0,49 m
e u = 0,029 m
De veerkracht (Fv = Cu) is dan gelijk aan het gewicht
van de klimmer: Cu = mg.
30000 × u = 90 × 9,81
u = 0,029 m
f 8,2 g
De vertraging bereken je met de snelheidsafname
Δv en de remtijd Δt die voor die afname nodig is. Na
4,0 m vrije val is de snelheid van de klimmer:
_1
_1 2
2
2
2 mv = mgh → 2 v = gh → v = 2gh = 2 × 9,81 × 4 =
78,5 → v = 8,9 m/s. De snelheidsafname Δv bij het
afremmen door het touw is 8,9 m/s.
De remtijd Δt bereken je als volgt:
De gemiddelde snelheid tijdens het afremmen is de
helft van de maximale snelheid: 4,45 m/s.
De remtijd Δt is dan de remafstand (0,49 m) gedeeld
door de gemiddelde snelheid (4,45 m/s):
Δt = 0,49 / 4,45 = 0,11 s.
De versnelling kun je nu uitrekenen:
a = Δv / Δt = 8,9 / 0,11 = 81 m/s2
1g = 9,81 m/s2 en 81 m/s2 = 81 / 9,81 = 8,2 g
g Bij dezelfde kracht rekt touw B 2 keer zo ver uit als
touw A. Touw A is 2 keer zo “stug” en de veerconstante van touw A is dan ook twee keer zo groot als
die van touw B. De eerste uitspraak is niet juist.
Beide touwen knappen bij dezelfde maximale kracht
Fmax. Touw A is dan 0,44 m uitgerekt en touw B 0,88 m.
De veerenergie bij die maximale kracht:
touw A _21 2Cu2 = C × 0,442 = 0,1936 × C
touw B _21 Cu2 = 0,5 × C × 0,882 = 0,3872 × C
De energie in touw B is het dubbele:
0,3872 / 1,936 = 2.
De tweede uitspraak is juist.
© Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_CH07.indd 77
h
kracht in N
80
70
60
50
40
30
20
10
0
0
5
10
15
20
25
30
uitrekking in cm
5,0
F ___
i 5 N: C = __
u = 1,2 = 4,2 N/cm
60
F ___
60 N: C = __
u = 18 = 3,3 N/cm
j De vislijn wordt slapper. Er is minder kracht nodig
voor een uitrekking van 1 cm.
k De lijn die hoort bij de draad van 10 m is zwart. Een 5
keer langere draad betekent een 5 keer slappere veer.
80
kracht in N
b Antwoord B: het oppervlak onder de kromme is de
arbeid die de “remkracht” heeft verricht en die
arbeid is weer gelijk aan de kinetische energie van
de auto. Door hokjes te tellen bepaal je dat oppervlak onder de grafiek.
70
60
50
40
30
20
10
0
0
5
15
20
25
30
uitrekking in cm
l De hoeveelheid opgenomen energie kan berekend
worden door het oppervlak onder de grafiek te
bepalen tot 80 N. Dit is te benaderen met een
driehoek: _21 × 80 × 0,265 = 10,6. De hoeveelheid
opgenomen energie is dus 10,6 J. De vislijn kan dus
10 J opnemen voordat hij knapt.
Door een driehoek te gebruiken onderschat je de energie
zelfs een beetje, het werkelijke oppervlak is groter.
38 a De banden moet veel grip hebben anders blaast de
wind de kar achteruit.
b Als het waait, draait de bovenste as met de wijzers
van de klok mee. Het elastiek brengt die draaiing
over op de wielen zodat de wagen naar links
beweegt.
c De windkracht verricht positieve arbeid. De snelheid
van de kar neemt namelijk toe.
d Een zeilboot die laveert tegen de wind.
77
15/07/13 6:27 PM
Hoofdstuk 7 Energie Omzetten
7.4 Zuinig met energie
1,6 · 104 L
Reken eerst uit hoeveel seconde een vlucht van
1000 km duurt: reistijd = 1000 km / 900 km/h = 1,11
uur = 1,11 × 3600 = 4000 s. Je houdt geen rekening
met start, landing, op snelheid komen en het
afremmen van het vliegtuig.
De hoeveelheid kerosine is dan:
10 mL × aantal stoelen × aantal seconde =
10 × 400 × 4000 = 16000000 mL = 16000 L = 1,6 · 104 L.
40
Een snelheid van 413 km/h = 115 m/s.
Er geldt: P = Fv
885 · 103 = F × 115 en F = 885 · 103 / 115 = 7,7 · 103 N
41
0,077 L/s
Het vermogen van de auto bij topsnelheid is
885 kW. Dit is het nuttige vermogen. Het totale
885
vermogen is dan ____
35 × 100 = 2528 kW. Per seconde
verbruikt de motor dus 25,28 · 103 J energie. De
verbrandingswarmte van benzine is 33 · 109 J/m3,
oftewel 33 · 106 J/L. Het
2,5 · 106
verbruik van de auto is _______
= 0,077 L/s
33 · 106
42
Ja dat klopt. Bij 50 km/h = 13,8 m/s lees je af uit de
grafiek dat de rolweerstand (de horizontale lijn)
groter is dan de luchtweerstand. Op de autobaan is
de snelheid 120 km/h = 33 m/s en bij die snelheid zie
je in de grafiek dat de luchtweerstand een stuk
groter is dan de rolweerstand
43 a Kijk in de grafiek bij 1100 kg: de rolweerstand is daar
130 N. Invullen in de formule geeft:
Frol = Crol · m · g → 130 = Crol × 1100 × 9,81
130
130
= 0,012
Crol = __________ = _____
1100 × 9,81 10791
b De eenheid aan de linkerkant is N. De eenheid van
mg is ook newton, want mg is het gewicht en dat is
ook een kracht. crol heeft derhalve geen eenheid.
c De zachte banden vervormen meer waardoor de
rolweerstand toeneemt. Het motorvermogen moet
dan ook toenemen om een bepaalde snelheid te halen.
De weerstandskrachten zijn immers toegenomen.
Meer motorvermogen wil zeggen: meer brandstof.
d 1) Minder massa zorgt voor minder rolweerstand:
zie figuur 7.46.
2) Een lichte auto heeft minder kracht nodig om te
versnellen en minder kracht is minder benzineverbruik.
44 a 458 N
De totale weerstand is de rolweerstand plus de
luchtweerstand: 100 + _21 cwAv2 = 100 + 0,5 × 1,29 ×
0,40 × 1,8 × (100/3,6)2 = 100 + 358 = 458 N.
b 14,4 km
De arbeid die verricht moet worden om 1 km (1000
m) met de auto te rijden is:
W = Fs = 458 × 1000 = 458000 J.
Eén liter benzine levert aan nuttige energie:
0,20 × 33000000J = 6600000 J.
Aantal km op 1L benzine:
6600000 / 458000 = 14,4 km.
78
242759_NAT 3E TF HAVO 4 UW_CH07.indd 78
45
Pulsje
46
Pulsje
47 a Een luchtschip vliegt veel lager dan een vliegtuig en
dichter bij de aarde is de dichtheid van de lucht
groter. Een vliegtuig vliegt in ijlere lucht.
b Voor de luchtweerstand geldt _21 cwAv2 en voor het
energiegebruik P = Fv.
Je rekent eerst de weerstandkracht Fw uit die gelijk is
aan de voortstuwende kracht F van de motoren.
P = Fv invullen geeft 3533000 = F (135/3,6)
3533000 = F (37,5) en F = Fw = 94213 N.
Vervolgens reken je de cw-waarde uit met de eerst
genoemde formule:
Fw = 94213 = _21 cwAv2 alles invullen:
94213 = _21 × 1,29 × cw × 1320 × 37,52
94213 = 1197281 × cw
cw = 94213 / 1197281 = 0,079
48 a Na 7,5 s. De snelheid neemt dan niet meer toe. De
luchtweerstand is dan gelijk aan de zwaartekracht
op het voorwerp: Fl = Fz = mg = 0,200 × 9,81 =
1,96 N = maximale luchtweerstand
b 1,5 s
Als de luchtweerstand de helft van de maximale
waarde is, is de nettokracht de helft van de zwaartekracht op het vallende voorwerp.
Fnetto = 1,96 − _21 × 1,96 = 0,98 N
De versnelling van het vallende voorwerp is dan
geen 9,81 m/s2 meer zoals in het begin van de val
maar de helft van 9,81 m/s2 is 4,91 m/s2.
Trek in de grafiek de lijn die hoort bij een versnelling
van 4,91 m/s2 en kijk waar de kromme even steil
loopt als de lijn met die vaste versnelling van 4,91
m/s2. Zie tekening.
25
snelheid in m/s
39
20
15
10
5
0
0
2
4
6
8
10
12
tijd in s
De doorgetrokken lijn is de lijn die hoort bij een
versnelling van 4,91 m/s2, na 4,0 s is de snelheid dan
namelijk 19,6 m/s. verschuif de doorgetrokken lijn
totdat hij aan de kromme raakt. De gestippelde lijn
valt samen met de kromme na 1,5 s. Na 1,5 s is de
steilheid van de kromme gelijk aan 4,91 m/s2. Na 1,5 s is
de luchtweerstand de helft van de maximale waarde.
c Op tijdstip t = 0 is de luchtweerstand 0, op t = 1,5 s
is de luchtweerstand 0,98 N en na 7,5 s is de
luchtweerstand maximaal: 1,96 N.
© Noordhoff Uitgevers bv
15/07/13 12:46 PM
Hoofdstuk 7 Energie Omzetten
b 1 knoop = 1852 m/uur = 1852/3600 m/s = 0,514 m/s
Wil je in de formule de snelheid in knopen invullen
dan vermenigvuldig je eerst met 0,514 want de
snelheid in m/s is de snelheid
__ in knopen maal 0,514.
v (in knoop) × 0,514 = 1,25 lw
Formule ombouwen:
__
0,514
v (in knoop) × _____
1,25 = lw
luchtweerstand in N
2,5
2,0
1,5
1,0
__
0,5
0
0
2
4
6
8
v (in knoop) × 0, 4112 = lw
Links en rechts kwadrateren:
v2 (in knoop) × 0,411 = lw
lw = v2 (in knoop) x 0,17
Controleren met de gegevens van vraag a):
lw = 102 × 0,17 = 17 m. Klopt!
10
12
tijd in s
49 a Bij het optrekken wordt kinetische energie opgebouwd:
_1
2
5
2
8
2 mv = 0,5 × 6 · 10 × (130/3,6) = 3,91 · 10 J.
Het compenseren van weerstandskracht Fw
over een afstand s van 197 km kost ook energie:
W = Fws = 50000 × 197000 = 9,85 · 109 J.
In totaal is dat voor die ene rit: 3,91 · 108 + 9,85 · 109
= 1,0 · 1010 J.
b Per stop is dat 3,91 · 108 J. Zie vraag a) En dat 15 keer:
15 × 3,91 · 108 = 5,9 · 109 J.
50 a 62 m/s
De steilheid van de plaatsgrafiek is de snelheid van
de parachutist. Teken de raaklijn in punt dat hoort
bij het tijdstip t = 12 s.
Toepassing
Opgave 1 Vallend kogeltje
1
0,15 m/s
De snelheid is gelijk aan de helling van de lijn want
het diagram is een afstandsdiagram (s,t-diagram).
De lijn gaat door de punten (0,35 s, 60 cm) en (1,1 s,
71 cm). De helling van de lijn is dan:
(0,71 − 0,60)/(1,1 − 0,35) = 0,11/0,75 = 0,15 m/s.
De snelheid 65 cm onder punt A is 0,15 m/s.
2
De snelheid is in dat punt al geen 0 m/s meer. Dat
zie je aan het feit dat de raaklijn in (0,0) niet
horizontaal loopt. Op tijdstip t = 0 s heeft het
kogeltje al een snelheid.
3
50 cm
Het kogeltje raakt de olie op tijdstip t = 0,25 s want
vanaf dat punt neemt de snelheid af tot t = 0,35 s en
daarna blijft de snelheid in de olie constant.
Op t = 0,25 s is de afstand onder punt A 50 cm.
4
26
Voor de “vloeistofweerstand” Fv geldt:
1
2
Fv = __
2 · Cw · A · V
In de olie is de beweging eenparig (zonder versnelling). Het gewicht in de olie van het kogeltje is gelijk
aan de weerstand Fv in de vloeistof.
Gewicht kogeltje in olie is dan:
0,90 × mg = 0,90 × 0,00051 × 9,81 = 4,50 · 10−3 N.
Dichtheid olie is 0,80 g/cm2 = 0,80 · 103 kg/m3.
De doorsnede A van het kogeltje is
A = πr2 = π × (0,25 · 10−2)2 = 1,96 · 10−5 m2.
Dit alles vul je in in de formule:
4,50 · 10−3 = 0,5 × 0,80 · 103 × cw × 1,96 · 10−5 × 0,152
4,50 · 10−3 = 1,76 · 10−4 × cw
cw = 4,50 · 10−3 / 1,76 · 10−4 = 26.
hoogte in m
1800
1400
1000
600
200
0
0
20
40
60
80
100 120
tijd in s
Voor de raaklijn geldt dat de hoogte afneemt met
1700 m in 27,5 s. De snelheid die bij de raaklijn hoort
is: v = 1700 / 27,5 = 62 m/s. De snelheid na 12 s is dus
ook 62 m/s.
b De snelheid is redelijk constant rond het tijdstip t =
12 s. De nettokracht is dus 0 en dat wil zeggen dat
de weerstandskracht gelijk is aan de zwaartekracht:
Fz = Fw = mg = 90 × 9,81 = 8,8 · 102 N.
c Voor de luchtweerstand geldt: Fw = _21 cwAv2.
Alle grootheden invullen:
8,8 · 102 = 0,5 × 1,29 × cw × 622
8,8 · 102 = 2479 × cw
cw = 8,8 · 102 / 2479 = 0,36
d De arbeid die de weerstandkracht heeft verricht,
heeft er voor gezorgd dat alle zwaarte-energie is
omgezet in warmte. De gevraagde arbeid is gelijk
aan de zwaarte-energie op t = 0 s.
Ez = mgh = 90 × 9,81 × 1600 = 1,4 · 106 J
__
__
51 a vr = 1,25 lw = 1,25 × 17 = 5,15 m/s
Binas: 1 zeemijl = 1852 m (tabel 5)
5,15 m/s = 18540 m/uur = 18540/1852 zeemijl/uur =
10 zeemijl/uur = 10 knoop
© Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_CH07.indd 79
Opgave 2 Golf
5
1,3 · 102 Hz
De laatste flits is op het moment dat de bal geraakt
wordt en dat is de 34 flits. Er zijn dus 33 intervallen
in 0,25 s. Dat zijn 33 × 4 = 132 flitsen in 1,0 s. De
frequentie is 132 Hz.
6
4,3 m
De lengte van de weg is de oppervlakte onder het
v,t-diagram.
79
15/07/13 12:46 PM
Hoofdstuk 7 Energie Omzetten
50
11
100 km/h = 100 / 3,6 = 27,8 m/s
De rolweerstand bij die snelheid is 100 N.
De luchtweerstand bij die snelheid is 400 N.
De totale weerstand is 500 N en dat is ook de kracht
die de motor moet uitoefenen.
12
De arbeid is kracht maal afstand:
W = F × s = 500 N × 1000 m = 500000 J = 5,0 · 105 J.
Per 1 km is dat 5,0 · 105 J.
13
20%
Ga uit van een afstand van bijvoorbeeld 100 km.
Het benzineverbruik is dan 7,7 L en dat geeft een
totale energie van 7,7 × 33 · 106 = 2,541 · 108 J. De
arbeid die de motor moet verrichten voor de 100 km
is 100 × 5,0 · 105 J = 5,0 · 107 J.
Het rendement is:
12
0
0,14
0,25
De oppervlakte is linker driehoek + rechthoek +
bovenste driehoek = 0,5 × 0,14 × 12 + 0,11 × 12 + 0,5 ×
0,11 × (50 – 12) = 0,84 + 1,32 + 2,145 = 4,305 = 4,3 m.
7
8
0,30
De bewegingsenergie van het uiteinde van de club
is _21 mv2 = 0,5 × 0,450 × 502 = 563 J.
De bewegingsenergie van de bal is
_1
2
2
2 mv = 0,5 × 0,085 × 63 = 169 J.
rendement = energie bal / energie club = 169 / 563
= 0,30 (30%)
67 J
Je berekent eerst de snelheid van de club na de slag.
Dat kan met de wet van behoud van impuls. Zie
Binas tabel 35 A. De impuls van de club voor de
botsing is:
p = mv = 0,45 × 50 = 22,5
De impuls van de bal na de botsing is:
0,085 x 63 = 5,36
De club heeft na de botsing dus nog een impuls van
22,5 – 5,4 = 17,1
mv = 17,1
0,45 × v = 17,1
v = 17,1/0,45 = 38 m/s.
De bewegingsenergie van de club na de slag is dus
1/2mv2 = 327 J
Voor de slag was de energie 563 J
Na de slag 327 + 169 = 496 J
Er is dus in warmte omgezet: 563 – 496 = 67 J.
Opgave 3 Auto
9
De massa van de auto bereken je met de formule
Fr = cr · m · g
In de grafiek lees je af dat die kracht 100 N is en cr =
0,012.
Invullen levert op:
100 = 0,012 × m × 9,81
m = 100 / (0,012 × 9,81) = 100/0,11772 = 849 kg =
8,5 · 102 kg.
10
0,40
De luchtweerstandcoëfficiënt bereken je met de
formule: Fw = _21 cwAv2.
Neem het punt F = 700 N en v = 37 m/s en vul de
gegevens in in de formule.
700 = _21 × 1,29 × cw × 2,0 × 372
700 = 1766 cw
cw = 700 / 1766 = 0,40
80
242759_NAT 3E TF HAVO 4 UW_CH07.indd 80
arbeid
____________
energietotaal
5,0 · 107
= _________8 = 0,20 = 20%
2,541 · 10
14
32 m/s
De totale wrijvingskracht is 640 N. De
luchtweestand is 100 N minder omdat de rolweerstand 100 N is. Fw = 540 N. Uit de grafiek lees je af dat
bij die luchtweerstand een snelheid hoort van 32 m/s.
15
9,7 L per 100 km
De arbeid die de motor nu moet verrichten per
100 km is:
W = F × s = 640 N × 100000 m = 64000000
J = 6,4 · 107 J. Het rendement is nog steeds 20% en
dat betekent dat er 5 maal meer energie de motor in
moet: 5 × 6,4 · 107 J = 3,2 · 108 J.
1 L benzine levert nog steeds 33 · 106 J.
Aantal liter dat nodig is om 3,2 · 108 J energie te
produceren:
3,2 · 108 J / 33 · 106 J = 9,7 L.
Het benzineverbruik bij deze snelheid is 9,7 L per
100 km.
Opgave 4 Model van energieomzetting
16 Computeropdracht
17
Computeropdracht
18
Computeropdracht
19
Computeropdracht
Opgave 5 Sprinkhaan
20 De kinetische energie bij het loskomen, is helemaal
omgezet in zwaarte-energie in het hoogste punt op
1,0 m.
Dit geeft de volgende energie vergelijking:
_1
2
2 mv = mgh
vereenvoudigen: _21 v2 = gh
en invullen:
_1 2
2 v = 9,81 × 1,0 = 98,1
v2 = 196
v = 14 m/s
© Noordhoff Uitgevers bv
15/07/13 12:46 PM
Hoofdstuk 7 Energie Omzetten
21
v = 4,8 m/s
De snelheid is de steilheid van de raaklijn aan de grafiek
op het tijdstip t = 0,25 s. Die steilheid is 4,8 m/s.
22
De parabool is dan niet symmetrisch in geval van
luchtweerstand. de valtijd is 1,25 − 0,75 = 0,50 s.
De stijgtijd van de sprinkhaan duurt: 0,75 − 0,25 =
0,50 s. De luchtweerstand is dus verwaarloosbaar
want het stijgen duurt even lang als het vallen.
23
De zwaarte-energie is mgh = 0,0062 × 9,81 × (1,22 +
0,04) = 0,0766 J.
Die 4,0 cm moet erbij geteld worden omdat de
zuignap 4 cm was ingedrukt en t1 hoort bij de
situatie waarin de sprinkhaan al 4,0 cm omhoog is
gekomen, zie figuur 7.73.
De veerenergie bepaal je uit de oppervlakte onder
de (F, u)-grafiek van 0 tot 4,0 cm. Om deze oppervlakte te kunnen bepalen moet een rechte lijn door
de meetpunten worden getrokken.
F in N
8
0,5 × 8,82
h = _________ = 3,95m
9,81
c
d
e
7
6
f
5
4
3
2
1
0
0
1
2
3
u in cm
4
De veerenergie is dan:
2 × 0,040 × 7,5 = 0,15 J.
rendement = 0,0766/0,15 = 0,51 (51%)
_1
Proefwerkopgaven
1 a 9,0 m/s
Gebruik het principe dat de door de (netto, voorwaartse) kracht van 45 N verrichtte arbeid wordt
omgezet in kinetische energie:
W = F · s = 45 × 50 = 2250 J,
dus Ek = 2250 J = _21 mv2
_____
v=
2 a Via veerenergie (buiging van de polsstok)
b 5,05 m
Je mag aannemen dat: Ez (boven) = Ek (beneden)
1
2
2
mgh = __
2 mv ⇒ 80 × 9,81 × h = 0,5 × 80 × 8,8
2250
_____
27,5 = 9,0 m/s
b 18 N
Ek = _21 mv2 = 0,5 × 55 × 72 = 1347,5 J
er is dus 2250 − 1347,5 = 902,5 J ‘verdwenen’:
de weerstandskracht heeft 902,5 J negatieve arbeid
verricht:
902,5 = Fw · s = Fw × 50 → Fw = 902,5 : 50 = 18 N.
Of: Ek = 1347,5 J dus W = Fnetto · s = 1347,5 J
→ Fnetto = 1347,5 : 50 = 27 N
de weerstandskracht is dus 45 − 27 = 18 N
c Rolweerstand en luchtweerstand.
Zijn zwaartepunt kan 3,95 m hoger komen dus op
3,95 + 1,10 = 5,05 m
2,6 · 103 J
Ek = _21 mv2 = 0,5 · 80 × 82 = 2560 J = 2,6 · 103 J
De arbeid die door de matras wordt verricht op de
atleet wordt gegeven door het oppervlak onder de
groene lijn. Omdat de rode lijn niet recht is, benaderen we de groene lijn door een rechte lijn door de
punten {0 cm;0 N} en {45 cm;13 · 103 N}. Het oppervlak onder deze lijn bedraagt 0,5 × 0,45 × 13 · 103 =
2925 J = 3 · 103 J.
De gevraagde arbeid is negatief omdat de kracht
tegen de beweging in werkt.
Er moet meer arbeid worden verricht omdat tijdens
het inveren van de matras nog steeds over 45 cm
zwaarte-energie wordt omgezet in kinetische
energie van de atleet.
Nu wordt de arbeid, die door de matras op de atleet
wordt verricht, gegeven door het oppervlak onder de
rode lijn. Dit oppervlak is veel kleiner dan het oppervlak
onder de groene lijn, dus de atleet krijgt veel minder
kinetische energie omhoog, dan waarmee hij neerkwam. Zijn snelheid is dus (gelukkig) ook veel kleiner.
De oppervlakte tussen de groene en de rode lijn geeft
dus de energie weer die bij het in- en weer uitveren
van de matras is omgezet in warmte.
3 a 80 N
De rolweerstand is dat deel van de totale weerstand
dat onafhankelijk is van de snelheid.
Bij v = 0 m/s kun je de rolweerstand dus aflezen uit
de grafiek.
b Fw = _21 cw Av2 . Kijk in de grafiek bij 20 m/s. De totale
weerstand is 400 N. De rolweerstand is en blijft
80 N. De luchtweerstand is dan 320 N. Vul alle
gegevens in in de formule:
320 = _21 × 1,29 × cw × 2,1 × 202
320 = 542 × cw
cw = 320 / 542 = 0,59
c 5,4 kW
v = 60 km/h = 16,7 m/s
Lees bij deze snelheid de totale weerstand af:
F = 300 N P = F · v = 300 × 16,7 = 5,0 · 103 W =
5,0 kW
d 52 km/h
Er kan 0,82 × 60 MJ = 49,2 MJ nuttige arbeid
verricht worden over een afstand van 200 km =
2,0 · 105 m.
Bereken F uit W = F · s
49,2 · 106
= 246 N
F = ________
2,0 · 105
Lees v af uit de grafiek: v = 14,5 m/s = 52 km/h
© Noordhoff Uitgevers bv
242759_NAT 3E TF HAVO 4 UW_CH07.indd 81
81
15/07/13 12:46 PM