MODULE 16. PLASVORMING EN VERDAMPING
De vrijzetting van een vloeistof leidt tot de vorming van een plas. Deze plas zal zich verspreiden over de
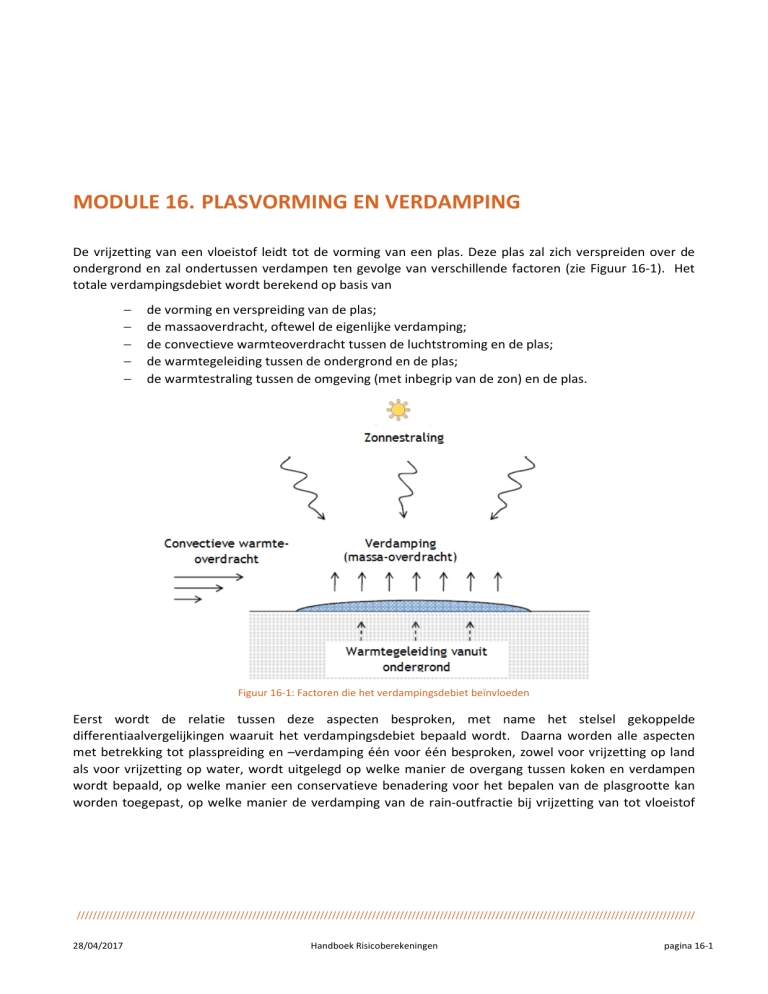
ondergrond en zal ondertussen verdampen ten gevolge van verschillende factoren (zie Figuur 16-1). Het
totale verdampingsdebiet wordt berekend op basis van
−
−
−
−
−
de vorming en verspreiding van de plas;
de massaoverdracht, oftewel de eigenlijke verdamping;
de convectieve warmteoverdracht tussen de luchtstroming en de plas;
de warmtegeleiding tussen de ondergrond en de plas;
de warmtestraling tussen de omgeving (met inbegrip van de zon) en de plas.
Figuur 16-1: Factoren die het verdampingsdebiet beïnvloeden
Eerst wordt de relatie tussen deze aspecten besproken, met name het stelsel gekoppelde
differentiaalvergelijkingen waaruit het verdampingsdebiet bepaald wordt. Daarna worden alle aspecten
met betrekking tot plasspreiding en –verdamping één voor één besproken, zowel voor vrijzetting op land
als voor vrijzetting op water, wordt uitgelegd op welke manier de overgang tussen koken en verdampen
wordt bepaald, op welke manier een conservatieve benadering voor het bepalen van de plasgrootte kan
worden toegepast, op welke manier de verdamping van de rain-outfractie bij vrijzetting van tot vloeistof
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
28/04/2017
Handboek Risicoberekeningen
pagina 16-1
verdichte gassen wordt meegenomen en met welk representatief verdampingsdebiet wordt verder
gewerkt in de dispersiemodellen.
Op het einde worden een aantal mogelijkheden tot beperking van de plasgrootte en de bepaling van het
vrijzettingspunt weergegeven.
16.1 SYMBOLEN
A
Atop
Awarmte
c0
cp
C
D
Deq
Dv
f
[m²]
[m²]
[m²]
[kg/m³]
[J/kg.K]
[-]
[m]
[m]
[m²/s]
[-]
F
FL
FT
g
g’
h
h
h'
he
hf
hf,max
hm
hmin
hp
[m/s²]
[m/s²]
[m/s²]
[m/s²]
[m/s²]
[m]
[W/m².K]
[W/m².K]
[m]
[m]
[m]
[m/s]
[m]
[m]
k
L
[W/m.K]
[m]
Oppervlakte van de plas
Oppervlakte van het bovenoppervlak van de plas
Warmtewisselend oppervlak
Concentratie van de verdampende stof aan het oppervlak van de plas
Specifieke warmte bij constante druk (lucht: 1001 J/kg.K bij 1,013 bar en 13°C)
Turbulente wrijvingscoëfficiënt
Diameter van een cirkelvormige plas
Equivalente plasdiameter bij een inkuiping
Molaire diffusiviteit
Factor die de radiale beweging van water onder de zich op water verspreidende
plas beschrijft
Wrijvingskracht
Laminaire wrijvingskracht
Turbulente wrijvingskracht
Valversnelling (9,81 m/s²)
Gereduceerde valversnelling
Gemiddelde hoogte van de plas
Gemiddelde convectieve warmteoverdrachtscoëfficiënt
Gemiddelde warmteoverdrachtscoëfficiënt
Gemiddelde dynamische hoogte van de plas
Plashoogte aan de rand van de plas
Hulpvariabele in de berekening van de plashoogte aan de rand van de plas
Massaoverdrachtscoëfficiënt
Minimale hoogte van de vloeistof in de plas
Gemiddelde hoogte van de individuele plassen, uitgemiddeld over de hele
landoppervlakte; oftewel het vloeistofvolume per oppervlakte-eenheid dat in de
plasjes van een ruwe ondergrond wordt vastgehouden
Warmtegeleidingscoëfficiënt (lucht: 0,023 W/m.K)
Lengte van een rechthoekige plas
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
28/04/2017
Handboek Risicoberekeningen
pagina 16-2
L’
m
mp
m MW
n
N
Pa
Pv
Pr
PrT
q q Q Q Q r
R
Re
Re0
s
Sc
ScT
t
T0
Tg
Tp
Tw
u∗
up
uw
V
z0
[-]
[kg/s]
[kg]
[kg/s]
[kg/mol]
[-]
[-]
[Pa]
[Pa]
[-]
[-]
[W/m²]
[W/m²]
[W]
[W]
Dimensieloze lengte van de plas
Vrijzettingsdebiet
Massa in de plas
Verdampingsdebiet
Molaire massa
Windprofielfactor
Hulpvariabele in de berekening van de vormfactor van de plas
Atmosferische druk
Verzadigingsdruk
Prandtlgetal (ν/α) (lucht: 0,708 bij 1,013 bar en 13 °C)
Turbulente Prandtl-getal (0,85)
Geleidingswarmteflux
Warmtestralingsflux
Convectieve warmteoverdrachtsvermogen
Warmtegeleidingsvermogen
[W]
Warmtestralingsvermogen
[m]
[J/mol.K]
[-]
[-]
[-]
[-]
[-]
[s]
[K]
[K]
[K]
[K]
[m/s]
[m/s]
[m/s]
[m³]
[m]
Straal van de plas
Universele gasconstante (8,3145 J/mol.K)
Reynoldsgetal u ∙ D/ν
Ruwheids Reynoldsgetal
Vormfactor van de plas
Schmidtgetal (ν/D )
Turbulente Schmidt-getal (0,85)
Tijd (vanaf de start van de vrijzetting)
Temperatuur van de bron
(Initiële) temperatuur van de grond
Temperatuur van de plas
Temperatuur van het water
Wrijvingssnelheid
Radiale snelheid van de plas
Windsnelheid op een hoogte van 10 m
Volume van de vloeistof in de plas
Ruwheidslengte
Griekse symbolen
αg
[m²/s]
Thermische diffusiviteit van de grond
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
28/04/2017
Handboek Risicoberekeningen
pagina 16-3
β
[-]
βh
[-]
∆c
∆Hv
∆T
ε
η
ηw
κ
λ
ν
νw
ρ
ρa
ρw
σ
χ
[kg/m³]
[J/kg]
[K]
[-]
[N.s/m²]
[N.s/m²]
[-]
[W/m.K]
[m²/s]
[m²/s]
[kg/m³]
[kg/m³]
[kg/m³]
[Pa]
[-]
Empirische functie in het concentratieprofiel; gebruikt bij massaoverdracht
Empirische functie in het concentratieprofiel; gebruikt bij convectieve
warmteoverdracht
Concentratieverschil tussen de omgeving en het oppervlak van de plas
Verdampingswarmte
Temperatuurverschil tussen de omgeving en het oppervlak van de plas
Dimensieloze parameter voor het effect van grond op de stroming
Dynamische viscositeit van de vloeistof in de plas
Dynamische viscositeit van het water (1,21.10-3 N.s/m² bij 13°C)
Constante van von Karman (0,4)
Thermische conductiviteit (geleidbaarheid) van de grond
Kinematische viscositeit (lucht: 1,45.10-5 m²/s bij 1,013 bar en 13 °C)
Kinematische viscositeit van water (1,21.10-6 m²/s bij 13°C)
Densiteit
Densiteit van de lucht
Densiteit van water (998,8 kg/m³ bij 13°C)
Oppervlaktespanning van de vloeistof in de plas in combinatie met water
Correctiefactor
16.2 VERDAMPINGSDEBIET
De oppervlakte van de plas en het verdampingsdebiet worden bepaald uit een stelsel gekoppelde
differentiaalvergelijkingen.
−
−
−
De verspreiding van de plas in functie van de tijd wordt gegeven door de vergelijkingen = ⋯ uit
§16.3.1. Hiermee wordt de oppervlakte van de plas bepaald.
De massabalans stelt dat de massa mp in de plas op elk ogenblik wordt bepaald door de vrijgezette
hoeveelheid m # (zoals bepaald in §15.2.2.4) verminderd met de verdampte hoeveelheid m. De
massabalans wordt gegeven door
$%&
= % # − %)
$'
De energiebalans stelt dat de temperatuur van de plas (en dus de thermische energie van de plas)
in de tijd wijzigt ten gevolge van warmtewisseling met de ondergrond, convectieve
warmteoverdracht en warmtestraling, ten gevolge van de warmte die wordt toegevoegd door de
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
28/04/2017
Handboek Risicoberekeningen
pagina 16-4
vrijgezette hoeveelheid en ten gevolge van de warmte die wordt verloren door verdamping van de
plas. De energiebalans wordt gegeven door
* ∙ + ∙ ,& ∙
$-&
= ./010223/ + .563)05
$'
20 + .#
9:
7123/ + % # ∙ 8 ,& - ∙ $- − %) ∙ Δ=) -& 9;
Het volledige stelsel differentiaalvergelijkingen wordt in rekening gebracht.
Indien er slechts een beperkte verdamping optreedt (weinig vluchtige vloeistoffen) en indien de vloeistof
vrijkomt bij omgevingstemperatuur, zal de temperatuur van de vloeistofplas ook tijdens het verdampen
nauwelijks verschillen van de omgevingstemperatuur. In dit geval volstaat een massabalans die stelt dat de
massa in de plas in de tijd wijzigt ten gevolge van o.a. het vrijzettingsdebiet en het verdampingsdebiet.
Indien het verdampingsdebiet echter zo hoog is dat hierdoor de temperatuur van de vloeistofplas daalt
onder de temperatuur van de omgeving (zeer vluchtige vloeistoffen), dient er naast een massabalans ook
een energiebalans opgesteld te worden. In deze energiebalans wordt er rekening gehouden met de
thermische energie van de vloeistof bij vrijzetting en met de warmtewisseling die optreedt tussen de plas
en de omgeving via geleiding (doorheen de ondergrond), via convectie (i.e. de wind), via straling (i.e. de
zonnestraling) en via verdamping.
16.3 PLASSPREIDING EN -VERDAMPING
Na vrijzetting zal de vloeistof zich over de ondergrond verspreiden o.i.v. de zwaartekracht. De straal van de
plas neemt toe in de tijd. Tijdens het verspreiden van de plas gaat de stof tegelijkertijd verdampen. Deze
aspecten zijn dus onlosmakelijk met elkaar verbonden.
De algemene principes zoals hieronder beschreven gelden voor alle bovengrondse installaties en voor
ondergrondse leidingen. Er wordt voor het bepalen van de plasgrootte geen onderscheid gemaakt tussen
boven- en ondergrondse leidingen. Voor ondergrondse tanks wordt in §16.4.1 specifiek aangegeven op
welke manier de plasgrootte moet bepaald worden.
Bij vrijzettingen uit verlaadinstallaties voor scheepsverladingen wordt ervan uitgegaan dat de gehele
vrijzetting op water terecht komt. Het betreft enkel de verlaadarmen en flexibels, niet de leidingen er
naartoe. Vrijzettingen uit de leidingen worden behandeld als vrijzettingen op land.
Bij vrijzettingen uit andere installaties waarbij verwacht wordt dat (deels) plasvorming op het water zal
optreden, wordt hier ook mee rekening gehouden. De eigen methodologie wordt in dit geval grondig
beschreven en gemotiveerd in het veiligheidsdocument.
Bij gebruik van een representatieve stof kan geen rekening gehouden worden met de mogelijke bezinking
van het product en met de oplosbaarheid van product in water, indien dit niet voor alle mogelijks
aanwezige stoffen van toepassing is.
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
28/04/2017
Handboek Risicoberekeningen
pagina 16-5
16.3.1 Plasspreiding
De formules van Webber (Webber, 1990), zoals hieronder uitwerkt, worden gebruikt voor de plasspreiding
in de tijd op land en op water. Hierbij worden de zwaartekracht, de inertiekracht en de wrijving met de
ondergrond in rekening gebracht.
Indien de methode van Webber niet mogelijk is, wordt tot nader order volgende methode toegepast.
De spreiding van de plas wordt bepaald met de eenvoudige formule van (DNV Software, 2006)
$>
= ?2 ∙ A ∙ ℎ − ℎC23 $'
Volgende minimale plashoogte hmin wordt gebruikt voor het berekenen van de plasgroottes op land en op
water:
−
−
−
25 mm voor onverharde grond en grind;
10 mm voor beton en verharde grond;
20 mm voor water (o.b.v. (TNO, 1988)).
Op het moment dat de minimale plashoogte wordt bereikt en er geen producttoevoer meer is naar de
plas, wordt aangenomen dat de straal terug afneemt en blijft de hoogte gelijk.
Om de plasspreiding van een vrijgezette vloeistof te berekenen met het model van Webber moet een
stelsel differentiaalvergelijkingen met bijbehorende beginvoorwaarden opgelost worden. Hierbij wordt ook
rekening gehouden met de verdamping uit de plas, die tegelijkertijd plaatsvindt.
Het model definieert een vormfactor s voor de plas en een wrijvingskracht F. De waarde van de vormfactor
bepaalt de invulling van een aantal functies. De waarde van de wrijvingskracht is afhankelijk van het type
ondergrond. Hieronder worden eerst een aantal algemene aspecten besproken, waarna wordt overgegaan
op de specifieke uitwerking voor plasspreiding op land en plasspreiding op water.
Op een gegeven moment, wanneer de radiale snelheid van de plas gelijk wordt aan 0 (bv. doordat de
verdampte hoeveelheid even groot is als de vrijgezette hoeveelheid), zal de plas stoppen met zich verder te
verspreiden. Hieronder wordt ook beschreven op welke manier dan wordt verder gewerkt.
16.3.1.1 Algemeen
16.3.1.1.1 Differentiaalvergelijkingen
Het berekenen van de plasspreiding komt neer op het oplossen van het stelsel differentiaalvergelijkingen.
$+
=⋯
$'
$>
=⋯
$'
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
28/04/2017
Handboek Risicoberekeningen
pagina 16-6
$D&
=⋯
$'
Voor een continue vrijzetting worden volgende beginvoorwaarden voorgesteld:
−
−
−
Volume: V = 0,001 m³;
Straal: r = 0,1 m;
Radiale snelheid: up = 1 m/s.
De beginvoorwaarden voor een instantane vrijzetting zijn het volume dat (instantaan) vrijkomt, de straal
van het initiële volume (bv. de straal van de opslagtank) en de initiële snelheid (waarvoor 1 m/s wordt
voorgesteld).
De invulling van het rechterlid van de eerste differentiaalvergelijking gebeurt afhankelijk van het type
vrijzetting. Voor een instantane vrijzetting waarbij geen verdamping in rekening wordt gebracht geldt
$+
=0
$'
Indien verdamping in rekening wordt gebracht tijdens de plasspreiding wordt deze uitdrukking
$+
%)
=−
$'
*
Voor een continue vrijzetting met een debiet %# waarbij geen verdamping in rekening wordt gebracht geldt
$+ %#
=
$'
*
Indien verdamping in rekening wordt gebracht tijdens de plasspreiding wordt deze uitdrukking
$+ %# %)
=
−
$'
*
*
De invulling van de rechterleden van de andere differentiaalvergelijkingen gebeurt afhankelijk van de aard
van de ondergrond, zoals hieronder beschreven.
16.3.1.1.2 Diepteprofiel van de plas
In het model wordt een dimensieloze vormfactor s gebruikt o.b.v. de plashoogte hf aan de rand van de plas
en de gemiddelde hoogte h.
s=
hf
h
Verder worden volgende functies van s gebruikt.
Indien G ≤ 2
ΨG = 1 − G
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
28/04/2017
Handboek Risicoberekeningen
pagina 16-7
KG = 1
Indien G > 2
GM
ΨG = − 4
2
KG = G
16.3.1.1.3 Wrijving met de ondergrond
De wrijvingskracht F is zodanig gedefinieerd dat deze hetzelfde teken heeft als up. De absolute waarde van
F is het maximum van de absolute waarden van de laminaire wrijvingskracht FL en de turbulente
wrijvingskracht FT.
O = max|O9 |, |OT |
D&
OT = K M G ∙ 2,53 ∙ , ∙ W ∙ M ∙ 1 − X
ℎ0
O9 = KG ∙ 4,49 ∙ Z ∙
D&M
ℎ0
Hierin hangen c en f af van de aard van de ondergrond, zoals verder beschreven.
Voor de turbulente wrijvingscoëfficiënt C wordt een waarde van 1,6.10-3 aangenomen.
16.3.1.1.4 Oppervlakte van de plas
De oppervlakte A van de plas wordt berekend als
[ = \ ∙ >M
16.3.1.1.5 Plasspreiding in combinatie met verdamping
Het verdampingsdebiet van een niet-kokende vloeistof wordt berekend met (zie ook §16.3.2)
%) = −ℎC ∙ [
6&
∙ ∆, ∙
^7
^)
∙ ln1 − ^)
^7
waarin Atop de oppervlakte van het bovenoppervlak van de plas is.
16.3.1.2 Plasspreiding op land
[
6&
= KG ∙ [ = KG ∙ \ ∙ > M
De plasspreiding op land op en nabij industriële sites betreft plasspreiding op ruwe oppervlakken. Voor
ruwe oppervlakken worden twee vloeistoflagen onderscheiden, met name een dynamisch deel met
gemiddelde hoogte he en een stilstaand deel dat de individuele plassen opvult, met gemiddelde hoogte hp
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
28/04/2017
Handboek Risicoberekeningen
pagina 16-8
van de individuele plassen, uitgemiddeld over de hele landoppervlakte.
oppervlakken
ℎ0 =
Hieruit volgt voor ruwe
+
− ℎ&
[
waarbij het volume in de plas bepaald wordt door de massabalans.
Voor hp worden volgende waarden gebruikt:
−
−
−
−
5 mm voor beton en stenen;
10 mm voor normale zandgrond, gravel en rangeerterreinen;
20 mm voor ruwe zandgrond, akkerland en grasland; en
25 mm voor zeer ruwe zandgrond met putten.
16.3.1.2.1 Differentiaalvergelijkingen
De straal van de plas volgt uit
met
$>
2
= D& ∙ 1 − ∙ Φε
$'
a
Φε = √1 + a − 1
a=
De radiale snelheid van de plas volgt uit
16.3.1.2.2 Diepteprofiel van de plas
8 ∙ D& M
A ∙ ℎ&
$D& 4 ∙ A ∙ ℎ0 ∙ ΨG
=
−O
$'
>
De vormfactor s wordt gegeven door
G = Φε ∙
16.3.1.2.3 Wrijving met de ondergrond
ℎ&
2 ∙ ℎ0
Voor plasspreiding op land geldt f = 0 en c = 3,0 zodat
OT = K M G ∙ 7,59 ∙ W ∙
16.3.1.3 Plasspreiding op water
D&
ℎ0M
Voor plasspreiding op water geldt
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
28/04/2017
Handboek Risicoberekeningen
pagina 16-9
ℎ = ℎ0 =
16.3.1.3.1 Differentiaalvergelijkingen
De straal van de plas volgt uit
De radiale snelheid van de plas volgt uit
met
+
[
$>
= D&
$'
$D& 4 ∙ A′ ∙ ℎ0 ∙ ΨG
=
−O
$'
>
A′ = A ∙
16.3.1.3.2 Diepteprofiel van de plas
*h − *
*h
De vormfactor s wordt gegeven door
G = i + ji M + k
met
ℎl,C7m
n
ℎ
M
r u 6 ∙ ν ∙ % #
ℎl,C7m = %op qj
;j
v
*∙\∙A
A∙*
Indien up > 0
i=
D&M
2,324 ∙ Aw ∙ ℎ
Indien up ≤ 0 (zie §16.3.1.4 voor de verdere uitwerking)
N=0
16.3.1.3.3 Wrijving met de ondergrond
Voor plasspreiding op water geldt c = 0,66 zodat
OT = K M G ∙ 1,67 ∙ W ∙
waarbij f berekend wordt uit de impliciete functie
D&
∙ 1 − X
ℎ0M
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
28/04/2017
Handboek Risicoberekeningen
pagina 16-10
met
x ∙ X y⁄M = 1 − X
x=
D& ∙ ℎ0M 1
{
∙j
∙
{h
Wh ∙ > KG
16.3.1.4 Einde plasspreiding
Het model van Webber (1990) laat toe de plasspreiding te berekenen tot het moment waarop de radiale
snelheid up = 0 en de plas een diepte hlim bereikt. Het daaropvolgende krimpen van de plas (omwille van de
verdamping) wordt berekend met (Brambilla & Manca, 2009).
+
>=j
\ ∙ ℎ12C
waarbij hlim gelijk is aan de waarde van he uit de formules voor de bepaling van de radiale snelheid van de
plas indien up = 0.
Concreet worden indien up ≤ 0 de differentiaalvergelijkingen voor de straal en de frontsnelheid (zowel voor
plasspreiding op land als op water) vervangen door
$>
1
$+
=
∙
$' 2 ∙ ?\ ∙ ℎ12C ∙ + $'
en
$D&
=0
$'
16.3.2 Massaoverdracht
Het verdampingsdebiet van een niet-kokende vloeistof wordt berekend met
%) = −ℎC ∙ [
waarbij Atop bepaald wordt volgens §16.3.1.1.5.
6&
∙ ∆, ∙
^7
^)
∙ ln1 − ^)
^7
Het concentratieverschil ∆c wordt gegeven door de concentratie c0 van de verdampende stof aan het
oppervlak van de plas, in de veronderstelling dat de concentratie van de verdampende stof in de
omgevende lucht nul is. Deze laatste wordt met behulp van de ideale gaswet berekend uit de
verzadigingsdruk van de vloeistof Pv.
,} =
~ ∙ ^) -& ∙ -&
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
28/04/2017
Handboek Risicoberekeningen
pagina 16-11
16.3.2.1 Rechthoekige plassen
Voor het berekenen van de massaoverdrachtscoëfficiënt hm wordt gebruik gemaakt van de uitdrukking van
(Kunsch, 1998).
ℎC = D∗ ∙
met
Z
=
ZM
3
,9
+ ∙ ∙ Z
∙ ZM ∙ w
M∙3
M ∙ ∙ 1 + ∙ 1 + 2 ∙
,9 ∙
⁄3
1
ZM = 1 + ∙
2 1+
w =
}
Voor het turbulente Schmidt-getal ScT wordt een waarde van 0,85 aangenomen.
De wrijvingssnelheid u∗ wordt bepaald als
D∗ =
∙ Dh
10
ln }
waarin uw de windsnelheid is op een hoogte van 10 m waarvoor de waarde overeenkomstig §3.3 wordt
bepaald (afhankelijk van de stabiliteitsklasse). De ruwheidslengte z0 wordt bepaald overeenkomstig §3.4.
De waarde voor n wordt middels een iteratieve procedure bepaald, waarbij
1
2
=
1
1
+
∙ lnZ
∙ ZM ∙ ′
2 1 + 2 ∙ 2
en waarbij als startwaarde voor ni de waarde 1/7 wordt gebruikt.
De waarde van β wordt bepaald als
= 7,3 ∙ }
Het ruwheids Reynoldsgetal wordt gegeven door
⁄
} =
waarin ν de kinematische viscositeit van lucht is.
∙ ,
⁄M − 5 ∙ ,9
D∗ ∙ }
W
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
28/04/2017
Handboek Risicoberekeningen
pagina 16-12
Indien bovenstaande methode niet mogelijk is, wordt tot nader order volgende methode toegepast.
Voor het berekenen van de massaoverdrachtscoëfficiënt op land wordt gebruik gemaakt van de
uitdrukking van (MacKay & Matsugu, 1973)
},
ℎC = 0,004786 ∙ Dh
∙ 2 ∙ >},
∙ , },
16.3.2.2 Cirkelvormige plassen
Kunsch gaat uit van een rechthoekige plas met een lengte L in de windrichting en eenheidsbreedte. Voor
een cirkelvormige plas, zoals deze die bekomen wordt voor de vrije plasspreiding met het model van
Webber (zie §16.3.1), met diameter D kan benaderend een vierkante plas genomen worden met een lengte
(en breedte) gelijk aan
=
√\
∙
2
Vervolgens kunnen de formules voor rechthoekige plassen (§16.3.2.1) gebruikt worden.
16.3.3 Convectieve warmteoverdracht
Het convectieve warmteoverdrachtsvermogen wordt als volgt berekend
.563)05
waarbij Atop bepaald wordt volgens §16.3.1.1.5.
20
= ℎ ∙ [
6&
∙ ∆-
16.3.3.1 Rechthoekige plassen
Voor het berekenen van de convectieve warmteoverdrachtscoëfficiënt wordt gebruikgemaakt van de
uitdrukking van (Kunsch, 1998)
ℎ = *7 ∙ ,& ∙ D∗ ∙
met
Z
=
ZM
3
^>
+ ∙ 9 ∙ Z
∙ ZM ∙ w
M∙3
M ∙ ∙ 1 + ∙ 1 + 2 ∙
^>9 ∙
⁄3
1
ZM = 1 + ∙
2 1+
w =
}
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
28/04/2017
Handboek Risicoberekeningen
pagina 16-13
De thermische en hydrodynamische eigenschappen zijn deze voor zuivere lucht. Voor het turbulente
Prandtl-getal PrT wordt een waarde van 0,85 aangenomen.
De wrijvingssnelheid u∗ wordt bepaald als
D∗ =
∙ Dh
10
ln }
waarin uw de windsnelheid is op een hoogte van 10 m waarvoor de waarde overeenkomstig §3.3 wordt
bepaald (afhankelijk van de stabiliteitsklasse).
De ruwheidslengte z0 wordt bepaald overeenkomstig §3.4.
De waarde voor n wordt middels een iteratieve procedure bepaald, waarbij
1
2
=
1
1
+
∙ lnZ
∙ ZM ∙ ′
2 1 + 2 ∙ 2
en waarbij als startwaarde voor ni de waarde 1/7 wordt gebruikt.
De waarde van βh wordt bepaald als
= 7,3 ∙ }
Het ruwheids Reynoldsgetal wordt gegeven door
⁄
} =
waarin ν de kinematische viscositeit van lucht is.
∙ ^>
⁄M − 5 ∙ ^>9
D∗ ∙ }
W
Indien bovenstaande methode niet mogelijk is, wordt tot nader order volgende methode toegepast.
Voor het berekenen van de convectieve warmteoverdrachtscoëfficiënt wordt gebruik gemaakt van de
formule uit (DNV Software, 2006):
∙ }, ∙ ^> },yy
−
voor een laminaire stroming (Re < 3,2.105)
−
voor een turbulente stroming (Re > 3,2.105)
ℎ = 0,037 ∙ ∙ }, − 15200 ∙ ^> },yy
ℎ = 0,664 ∙
De thermische en hydrodynamische eigenschappen zijn deze voor zuivere lucht. Het Prandtlgetal is dus
gelijk aan 0,72.
16.3.3.2 Cirkelvormige plassen
Kunsch gaat uit van een rechthoekige plas met een lengte L in de windrichting en eenheidsbreedte. Voor
een cirkelvormige plas, zoals deze die bekomen wordt voor de vrije plasspreiding met het model van
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
28/04/2017
Handboek Risicoberekeningen
pagina 16-14
Webber (zie §16.3.1), met diameter D kan benaderend een vierkante plas genomen worden met een lengte
(en breedte) gelijk aan
=
√\
∙
2
Vervolgens kunnen de formules voor rechthoekige plassen (§16.3.2.1) gebruikt worden.
16.3.4 Warmtegeleiding
Het warmtegeleidingsvermogen is het product van de warmtegeleidingsflux en het warmtewisselend
oppervlak.
16.3.4.1 Warmtegeleiding op land
./010223/ = /010223/ ∙ [h7C
0
Voor het berekenen van de warmtegeleidingsflux op land wordt gebruik gemaakt van de uitdrukking van
(Briscoe & Shaw, 1980) voor een plas die zich radiaal verspreidt
/010223/ =
∙ ∙ -/ − -&
?\ ∙ /
waarin t’ de tijd is waarop de plas de straal r’ bereikt.
∙8
}
2 ∙ \ ∙ >′ ∙ $>′
√' − '′
Voor specifieke situaties waarbij uitgegaan wordt van de maximale plas wordt gebruik gemaakt van de
uitdrukking voor een plas die zich niet verspreidt
/010223/ =
∙ ∙ -/ − -&
?\ ∙ / ∙ '
Voor een indringbare ondergrond wordt de correctiefactor χ gelijk gesteld aan 2,63 en voor een nietindringbare ondergrond aan 1. Dit is samen met de eigenschappen van de ondergrond met betrekking tot
warmtegeleiding weergegeven in Tabel 16-1 (van den Bosch, 2005) voor de meest voorkomende
ondergronden. In specifieke gevallen kan gebruik gemaakt worden van de andere ondergronden uit (van
den Bosch, 2005).
Tabel 16-1: Warmtegeleidingseigenschappen van verschillende ondergronden
Materiaal
Beton
Onverharde grond
Grind
λ
[W.m.K]
1,3
0,9
2,5
ρ
[kg/m³]
2400
2500
2000
Cp
[J/kg.K]
920
836
1140
αg
[m²/s]
5,9 10-7
4,3 10-7
1,1 10-6
χ
[-]
1
2,63
2,63
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
28/04/2017
Handboek Risicoberekeningen
pagina 16-15
16.3.4.2 Warmtegeleiding op water
De warmtegeleidingsflux op water wordt gegeven door volgende formule
/010223/ = ℎ′ ∙ -h − -& waarbij voor h’ een empirisch bepaalde waarde van 500 W/m².K gebruikt wordt (van den Bosch, 2005).
16.3.4.3 Warmtewisselend oppervlak
Voor bovengrondse installaties is het warmtewisselend oppervlak gelijk aan de plasoppervlakte.
Voor ondergrondse tanks (inclusief ingeterpte tanks) is het warmtewisselend oppervlak gelijk aan de som
van alle oppervlakten (wanden, bodem, dak) van de tank in contact met de bodem vóór de installatie faalt.
16.3.5 Warmtestraling
Het warmtestralingsvermogen is het product van de warmtestralingsflux en het warmtewisselend
oppervlak.
.#
7123/
Voor de waarde voor de warmtestralingsflux #
= #
7123/
∙ [h7C
7123/ wordt
0
deze van de zonnestraling uit §3.1 genomen.
Het warmtewisselend oppervlak is gelijk aan de plasoppervlakte.
16.3.6 Overgang tussen koken en verdampen
Voor kokende vloeistoffen wordt verondersteld dat de temperatuur in de plas constant is. De overgang van
een kokende naar een niet-kokende plas wordt gemaakt op het ogenblik dat het verdampingsdebiet van de
niet-kokende plas groter wordt dan het verdampingsdebiet van de kokende plas. Het verdampingsdebiet
van de niet-kokende plas wordt berekend bij een verzadigingsdruk gelijk aan 950 mbar.
16.3.7 Conservatieve benadering
In specifieke situaties, zoals wanneer een conservatieve berekening wordt uitgevoerd om aan te tonen dat
een bepaald scenario geen effecten buiten genereert, kan voor de eenvoud gewerkt worden met de
maximale plas die kan gevormd worden. Hierbij wordt enkel rekening gehouden met de vrijgezette
hoeveelheid en met een ondergrens voor de plashoogte.
De ondergrens voor de plashoogte kan bepaald worden uit
∙∙C
1. De uitdrukking o.b.v. de viscositeit en het brondebiet, zijnde ∙∙/, die enkel geldig is voor continue
u
vrijzettingen die 1800 s aanhouden;
2. De ruwheid van de ondergrond, gekenmerkt door hp, die enkel relevant is voor plasspreiding op land.
Dit impliceert dat een ondergrens voor de plashoogte bepaald kan worden op basis van Tabel 16-2.
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
28/04/2017
Handboek Risicoberekeningen
pagina 16-16
Tabel 16-2: Bepaling ondergrens plashoogte
Continue vrijzettingen
Op land en gedurende 1800 s
Op land en gedurende minder dan 1800 s
u 6 ∙ ν ∙ % #
~op q j
,ℎ v
*∙\∙A &
6 ∙ ν ∙ % #
j
*∙\∙A
u
Op water en gedurende 1800 s
Op water en gedurende minder dan 1800 s
Instantane vrijzettingen
Op land
Op water
ℎ&
Berekeningen volgens §16.3.1.3
ℎ&
Berekeningen volgens §16.3.1.3
16.3.8 Verdamping rain-outfractie
Bij vrijzetting van tot vloeistof verdichte gassen wordt enerzijds een wolk gevormd op basis van de flash- en
sprayfractie en wordt anderzijds een plas gevormd op basis van de rain-outfractie. De rain-outfractie vormt
een kokende plas op de grond waarvan de plasoppervlakte berekend wordt op basis van de hoeveelheid
rain-out en de ondergrens voor de plashoogte volgens §16.3.7. De verdamping hiervan moet ook in
rekening gebracht worden. Dit gebeurt op dezelfde manier als beschreven in §16.2 t.e.m. §16.3.5. De
manier waarop de twee afzonderlijke brontermen, met name de wolk op basis van de flash- en sprayfractie
en de wolk op basis van de verdamping van de rain-outfractie, moeten worden gecombineerd, wordt
hieronder uitgelegd voor ontvlambare stoffen enerzijds en toxische stoffen anderzijds.
16.3.8.1 Ontvlambare stoffen
Voor ontvlambare stoffen worden de dispersieberekeningen van de instantaan gevormde wolk en van de
plasverdamping afzonderlijk uitgevoerd. Vervolgens worden de concentraties van beide berekeningen op
elk tijdstip opgeteld.
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
28/04/2017
Handboek Risicoberekeningen
pagina 16-17
Indien bovenstaande methode niet mogelijk is, wordt tot nader order volgende methode toegepast.
Bij instantaan falen wordt onmiddellijk een wolk gevormd op basis van de flash- en sprayfractie. Voor
brandbare stoffen wordt de verdampingshoeveelheid van de rain-outfractie opgeteld bij de wolk zolang de
initiële wolk zich boven de plas bevindt. Dit wordt gemodelleerd als zijnde tot wanneer de LEL-contour
van de initiële wolk voorbij het vrijzettingspunt is. Wanneer de wolk van de plas is weggedreven, vormt
deze verdampingshoeveelheid een afzonderlijke pluim. Deze moet niet verder beschouwd worden in de
berekeningen. Als de initiële wolk de LEL niet bereikt, wordt enkel plasverdamping toegepast op de
rainout-fractie.
Voor continue vrijzettingen wordt de gebruikte methode beschreven in het veiligheidsdocument.
16.3.8.2 Toxische stoffen
Voor toxische stoffen worden de dosissen van de initiële wolk en de afzonderlijke pluim ten gevolge van
verdamping van de rain-outfractie gedurende 30 minuten afzonderlijk bepaald en opgeteld.
16.3.9 Representatief verdampingsdebiet
Voor het bepalen van het representatief verdampingsdebiet en de bijhorende representatieve waarden om
mee verder te werken in het dispersiemodel wordt de verdampingscurve (beperkt tot 1800 s), zijnde het
verdampingsdebiet in functie van de tijd, ingedeeld in 5 tijdssegmenten, zodanig dat de massa die
verdampt in elk segment gelijk is.
In de berekeningen wordt gewerkt met het representatieve segment. Voor ontvlambare stoffen is dit het
segment met het hoogste gemiddelde verdampingsdebiet. Voor toxische stoffen is dit het segment met
het tweede hoogste gemiddelde verdampingsdebiet.
Van dit representatieve segment wordt het gemiddelde verdampingsdebiet genomen om verder te
rekenen. Voor de andere gerelateerde parameters, zoals de temperatuur, de druk, de densiteit, de
plasdiameter, wordt de waarde genomen horende bij het representatieve segment (zie Figuur 16-2).
De tijdsduur van het representatieve segment komt overeen met 1/5e van de representatieve
verdampingsduur. Dit betekent dat de verdampingsduur wordt aangepast op basis van de tijdsduur van
het representatieve segment, zodat de totale verdampte massa ongewijzigd is.
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
28/04/2017
Handboek Risicoberekeningen
pagina 16-18
Representatief verdampingsdebiet voor
ontvlambare stoffen
Verdampingsdebiet [kg/s]
Tijdstip voor bepalen representatieve
temperatuur, druk, enz. (voor toxische
stoffen)
Representatief verdampingsdebiet
voor toxische stoffen
Oppervlakte = 20% van vrijgezette
massa
e
1/5 van representatieve duur (voor
toxische stoffen)
Tijd [s]
Figuur 16-2: Bepaling van het representatief verdampingsdebiet
16.4 PLASBEPERKING
De plas zoals hierboven berekend kan in een aantal gevallen in oppervlakte beperkt worden, zoals bij
ondergrondse tanks, bij de aanwezigheid van een inkuiping of opvangvoorzieningen.
16.4.1 Ondergrondse tanks
Plasvorming bij ondergrondse tanks voor niet-kokende vloeistoffen (bij omgevingstemperatuur) wordt niet
beschouwd.
Voor de bepaling van de plasgrootte bij andere ondergrondse tanks wordt uitgegaan van de oppervlakte
van de tank gezien vanuit bovenaanzicht. Dit geldt enkel voor tanks die onder het maaiveld gelegen zijn.
Een ingeterpte tank wordt voor dit aspect als een bovengrondse tank beschouwd, omdat bij falen
verondersteld wordt dat de interpende aarde verdwijnt en dus dat de inhoud van de tank niet opgevangen
wordt.
16.4.2 Aanwezigheid van een inkuiping
De grootte van de plas in een inkuiping wordt beperkt door de maximale plasoppervlakte van de inkuiping.
De regels zoals hieronder beschreven worden gehanteerd.
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
28/04/2017
Handboek Risicoberekeningen
pagina 16-19
16.4.2.1 Maximale plasoppervlakte
Voor het bepalen van de maximale plasoppervlakte kan conservatief gewerkt worden met de brutooppervlakte van de inkuiping, zolang de omstandigheden dit toelaten (bv. om aan te tonen dat de
effectafstand niet buiten de terreinsgrens komt). Anders wordt onderstaande werkwijze toegepast.
Voor het vervolgscenario plasbrand in de inkuiping wordt voor alle faalwijzen die leiden tot een volledig
gevulde inkuiping gerekend met de bruto-oppervlakte van de inkuiping (vermenigvuldiging van lengte en
breedte van de inkuiping voor een rechthoekige inkuiping) als maximale plasoppervlakte.
Voor de maximale plasoppervlakte bij de andere vervolgscenario’s, zoals toxische wolk, wolkbrand en
gaswolkexplosie, wordt volgende werkwijze afhankelijk van de faalwijze toegepast:
−
−
Voor een continue vrijzetting is de maximale plasoppervlakte gelijk aan de netto-oppervlakte van
de inkuiping, zijnde de bruto-oppervlakte van de inkuiping min de grondoppervlakte van alle
aanwezige tanks;
Voor een instantane vrijzetting is de maximale plasoppervlakte de netto-oppervlakte plus de
oppervlakte van de tank waaruit de vrijzetting gebeurt. Indien (conservatief) meerdere tanks
samen worden genomen, wordt de oppervlakte van de tank met de grootste grondoppervlakte
gebruikt.
16.4.2.2 Vorm van de plas
Voor kuipbranden wordt met de werkelijke vorm van de inkuiping gewerkt.
Indien bovenstaande methode niet mogelijk is, wordt tot nader order volgende methode toegepast.
Voor kuipbranden wordt met cirkelvormige plassen gewerkt en wordt de maximale plasoppervlakte
omgerekend naar een equivalente plasdiameter. Volgende formule wordt gebruikt:
[
0 = 2 ∙ j
\
Voor rechthoekige inkuipingen met een lengte/breedte-verhouding groter dan 2 wordt de inkuiping
ingedeeld in zo weinig mogelijk fictieve inkuipingen met elk een lengte/breedte-verhouding kleiner dan of
gelijk aan 2. De totale oppervlakte van alle fictieve inkuipingen samen moet gelijk zijn aan de oppervlakte
van de volledige inkuiping. Voor elk van deze oppervlaktes wordt de equivalente plasdiameter
uitgerekend zoals hierboven.
Voor het berekenen van de effecten van plasbrand wordt de stralingswarmteflux van de volledige
oppervlakte berekend, alsof er geen opsplitsing is in verschillende fictieve inkuipingen. Deze
stralingswarmteflux wordt vervolgens toegepast voor de verschillende fictieve inkuipingen.
Voor niet-rechthoekige inkuipingen wordt een gelijkaardige methodiek toegepast. Deze wordt beschreven
in het veiligheidsdocument.
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
28/04/2017
Handboek Risicoberekeningen
pagina 16-20
16.4.3 Verlaadplaatsen voor tankwagens en spoorwagons
Op voorwaarde dat er voldoende opvangvoorzieningen zijn, mag de plasoppervlakte op een verlaadplaats
voor tankwagens beperkt worden tot 1200 m² en op een verlaadplaats met grind voor spoorwagons tot
600 m². De motivering dient toegevoegd te worden in het veiligheidsdocument.
16.4.4 Aanwezigheid van hellingen en opvangvoorzieningen
Opvangvoorzieningen en hellingen kunnen de plasgrootte na vrijzetting van een stof beperken of de plas in
een bepaalde richting sturen.
Gesloten opvangvoorzieningen, zijnde opvangvoorzieningen waaruit geen (relevante) verdamping kan
ontsnappen, kunnen in rekening gebracht worden bij het bepalen van de plasgrootte door rekening te
houden met de inhoud van de opvangvoorziening. Voorwaarde is dat de opvangvoorziening steeds leeg is.
Indien dit niet het geval is, kan de plasoppervlakte of de vrijgezette hoeveelheid niet beperkt worden.
Uitzondering hierop zijn opvangvoorzieningen die juist wel gevuld moeten zijn met een bepaalde stof om
verspreiding tegen te gaan. In dit geval wordt een grondige motivering en beschrijving toegevoegd.
Hellingen worden bij voorkeur niet in rekening gebracht, maar het is toegelaten mits toevoeging van
geometrische berekeningen om aan te tonen hoe groot de plas zal zijn.
De motivering en werkwijze voor zowel de gesloten opvangvoorzieningen als voor de hellingen worden
beschreven in het veiligheidsdocument.
16.4.5 Plasbeperking op water
De plas zoals hierboven berekend kan in een aantal gevallen in oppervlakte beperkt worden, zoals bij de
aanwezigheid van vlottende dammen. Het in rekening brengen van plasbeperkende maatregelen kan enkel
mits grondige motivatie. Deze wordt uitgebreid beschreven in het veiligheidsdocument.
16.5 VRIJZETTINGSPUNT
Het vrijzettingspunt wordt bepaald volgens de principes in §15.2.3. Hier worden een aantal specifieke
gevallen behandeld, zoals een vrijzetting binnen een inkuiping en een vrijzetting op water.
16.5.1 Bij vrijzetting op land
Bij een tank zonder inkuiping wordt de (x, y)-coördinaat van het vrijzettingspunt gelijkgesteld aan het
midden van de tank (cfr. §15.2.3).
Bij aanwezigheid van een inkuiping wordt voor elke tank in de inkuiping het vrijzettingspunt gelijkgesteld
aan het middelpunt van de inkuiping onafhankelijk van de grootte van de plas. Specifieke situaties kunnen
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
28/04/2017
Handboek Risicoberekeningen
pagina 16-21
echter aanleiding geven tot andere vrijzettingspunten. Dit dient beschreven en gemotiveerd te worden in
het veiligheidsdocument.
Indien voor kuipbrand niet met de vorm van de inkuiping gewerkt wordt (tot nader order) (zie §16.4.2.2),
geldt het volgende.
Bij rechthoekige inkuipingen die ingedeeld worden in fictieve inkuipingen met een lengte/breedteverhouding kleiner dan of gelijk aan 2 wordt het vrijzettingspunt telkens gelijkgesteld aan het middelpunt
van deze fictieve inkuipingen.
16.5.2 Bij vrijzetting op water
Het vrijzettingspunt, het middelpunt van de plas, wordt gelegd op de grens tussen land en water ter hoogte
van de verlading (zie Figuur 16-3). Voor het bepalen van het vrijzettingspunt wordt de steiger als land
beschouwd, zodat het vrijzettingspunt aan het schip gelegen is.
Figuur 16-3: Vrijzettingspunt bij verladingen op de kade
16.6 VERSIEBEHEER
Datum
Versie
April ‘17
1.0
Voornaamste aanpassingen
1e versie
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
28/04/2017
Handboek Risicoberekeningen
pagina 16-22










